Правило Варнсдорфа

В 1823 году Варнсдорф в брошюре «Простейшее и наиболее общее решение задачи о ходе коня» предложил следующее правило обхода доски размером 88.

На каждом ходу ставь коня на такое поле, из которого можно совершить наименьшее число ходов на еще не пройденные поля. Если таких полей несколько, разрешается выбирать любое из них.

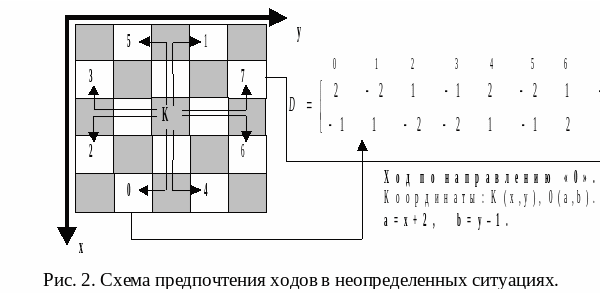
Долгое время о его справедливости не было известно каких-либо конкретных утверждений. Опровержение правила Варнсдорфа приведено в [6, с. 28, 29]. Иными словами, с какого бы поля конь ни начал движение, следуя правилу Варнсдорфа, его можно завести в тупик до полного обхода доски. Добавлением дополнительных ограничений к правилу Варнсдорфа можно получать те или иные алгоритмы перемещения коня по доске (возможно, и не приводящие к её обходу). Делать это можно фиксированием конкретного вида матрицы приращений D, используемой для получения кандидатов на очередной ход, и правила однозначного выбора хода в неопределенных ситуациях. Как мы уже отмечали, зафиксировать D можно 40320 способами. На рис. 2 указан один из них. При наличии нескольких допустимых ходов условимся выбирать тот из них, который сформирован с помощью самого левого столбца D. При фиксированной матрице D соответствующий алгоритм перемещения коня назовем D-алгоритмом.

Обход доски конем d-алгоритмом

Постановка задачи. Пусть D зафиксировано, и на шахматной доске размера nn в позиции (x, y) находится конь. Cоставить рекурсивную программу-функцию, находящую D-алгоритмом обход доски конем, если он существует. При отсутствии обхода должна быть выдана «тупиковая позиция» – матрица-доска с уже зафиксированным неполным обходом.

Решение. Функции ClockW и Vans решают поставленную задачу (см. Примеры программ).

3. Примеры программ

Обход шахматной доски конём:

const NN = 8;

type matr = array [0..1,0..7] of integer;

type Matrix = array [0..7,0..7] of integer;

var D: matr;

function HTour (n,x,y,boo,j:integer; H:Matrix):integer;

var k,a,b:integer;

begin

k:=0;

while ( k<=7 ) and (boo = 0) do

begin

a:=x+D[0,k];

b:=y+D[1,k];

if (((a>=0) and (a<=(n-1))) and ((b>=0)and(b<=(n-1)))and(H[a,b]=0)) then

begin

H[a,b]:=j;

boo:=1;

if (j<n*n) then

begin

boo:=HTour (n,a,b,0,j+1,H);

if (boo = 0) then

H[a,b]:=0;

end;

end;

k:=k+1;

end;

result:= boo;

end;

function HMain (n,x,y:integer; M:Matrix):integer;

var boo,i,j:integer; H:Matrix;

begin

for i:=0 to NN-1 do

for j:=0 to NN-1 do

H[i,j]:=0;

H[x,y]:=1;

boo:=HTour (NN,x,y,0,2,H);

for i:=0 to NN-1 do

for j:=0 to NN-1 do

M[i,j]:=H[i,j];

result:=boo;

end;

procedure Vans(n,x,y:integer; var H:Matrix;j:integer);

var k,a,b,aa,bb,numk,nums,s,boo,u,v:integer;

begin

numk:=8;

Writeln(n,x,y,j);

for k:=0 to 7 do

begin

writeln(k);

a:=x+D[0,k];

b:=y+D[1,k];

writeln(a,b);

nums:=0;

if (((a>=0)and(a<=(n-1)))and((b>=0)and(b<=(n-1)))and(H[a,b]=0)) then

begin

for s:=0 to 7 do

begin

writeln(s);

u:=a+D[0,s];

v:=b+D[1,s];

writeln(u,v);

if ((u>=0)and(u<=(n-1)))and((v>=0)and(v<=(n-1)))and(H[u,v]=0) then

nums:=nums+1;

end;

if (nums<numk) then

begin

numk:=nums;

aa:=a;

bb:=b;

writeln(aa,bb)

end;

end;

end;

if (numk<8) then

begin

writeln(aa,bb,j);

H[aa,bb]:=j;

Vans(n, aa, bb, H, j+1);

end;

end;

procedure ClockW(n, x, y:integer; var M:Matrix);

var H:Matrix;

i,j: integer;

begin

i:=0;

for i:=0 to 7 do

for j:=0 to NN-1 do

H[i,j]:=0;

H[x,y]:=1;

Vans(NN, x, y, H, 2);

for i:=0 to n-1 do

for j:=0 to n-1 do

M[i,j]:=H[i,j];

end;

var M:Matrix; i,j:integer;

begin

D[0,0]:= 1; D[0,1]:= -1; D[0,2]:= -2;

D[0,3]:= -2; D[0,4]:= -1; D[0,5]:= 1;

D[0,6]:= 2; D[0,7]:= 2;

D[1,0]:= 2; D[1,1]:= 2; D[1,2]:= 1;

D[1,3]:= -1; D[1,4]:= -2; D[1,5]:= -2;

D[1,6]:= -1; D[1,7]:= 1;

Нерекурсивный вариант схемы перебора с возвратом для нахождения всех решений (Схема 1):

begin (* Нерекурсивный вариант схемы перебора с возвратом.*)

(* Нахождение всех решений. *)

j := 0;

while j  0 do

if просмотрены не все элементы M_j then

begin

w := очередной непросмотренный элемент M_j ;

Элемент w объявляется просмотренным ;

if G(v₀, v₁, …, v_{j – 1}, w) = true then (* если частичное

решение *)

if (v₀, v₁, …, v_{j – 1}, w)^T – полное решение задачи then

write ( (v₀, v₁, …, v_{j – 1}, w)^T );

else

begin

v_j := w;

if j < n – 1 then j := j + 1;

end

end

else

j:=j–1(* Возврат к более короткому частичному решению *)

(* Все элементы M_j становятся непросмотренными *)

end

Рекурсивный вариант схемы перебора с возвратом для нахождения всех решений (Схема 2):

procedure backtracking ( j );

(* Рекурсивный вариант схемы перебора с возвратом *)

(* Нахождение всех решений расширением (v₀, v₁, …, v_{j – 1})^T *)

(* Массив v – глобальный *)

begin

for w  M_j do

if G(v₀, v₁, …, v_{j – 1}, w) = true then

begin

v_j := w;

if v  (v₀,v₁,…,v_{j – 1}, w)^T–решение задачи then write (v);

else if j < n – 1 then backtracking ( j + 1);

end

end

Рекурсивный вариант схемы перебора с возвратом для нахождения одного решения (Схема 3):

procedure backtracking ( j, pri );

(* Рекурсивный вариант схемы перебора с возвратом. *)

(* Нахождение одного решения расширением (v₀, v₁, …, v_{j – 1})^T . *)

(* Массив v – глобальный. *)

begin

while ( просмотрены не все элементы M_j ) and

( pri = ’решение не найдено’) do

if G(v₀, v₁, …, v_{j – 1}, w) = true then

begin

v_j := w;

if v  (v₀, v₁, …, v_{j – 1}, w)^T – решение задачи

then

begin

write (v);

pri := ’решение найдено’;

end

else

if j<n–1 then backtracking (j+1, pri);

end

end