Тема 2.3

ИНДЕКСЫ

Общее понятие об индексах и значение индексного метода анализа. Индексы индивидуальные и общие, простые и аналитические. Сводные индексы. Индексы количественных показателей. Индексы качественных показателей. Индексные системы в динамике. Средние формы сводных индексов. Разложение абсолютных приростов по факторам. Использование индексов в территориальных сравнениях. Использование индексов в экономическом анализе и в макроэкономических исследованиях. Методы расчета и анализа индексов цен. Методы оценки уровня и динамики инфляции

Индекс – это относительная величина сравнения, которая характеризует изменения явлений и процесов во времени, в пространстве или по сравнению с планом (нормой, стандартом).

Посредством индексов решают задачи:

1.Дать обобщающую характеристику изменения одноименного показателя по разнородной совокупности;

2.Провести анализ влияния отдельных факторов на изучаемое явление;

3.Дать оценку динамики среднего показателя по однородной совокупности, в том числе за счет изменения структуры.

Индексы классифицируются по следующим направлениям:

1. По выбранной базе сравнения (динамические, территориальные и по сравнению с планом).

2. По степени агрегирования (или охвата) явления (индивидуальные и сводные).

3. По форме построения сводных индексов (общие и групповые).

4. По характеру исследуемой величины.

5. По виду весов , выбранных в индексе ( Пааше, Ласпейреса).

Введем условные обозначения, используемые в теории индексного метода:

i - индивидуальный индекс; I – сводный индекс; p – цена единицы товара; q - количество товара в натуральном выражении; z – себестоимость продукции; t - трудоемкость единицы продукции; T - общие затраты времени; 1- подстрочный символ показателя текущего (отчетного) периода; 0 - подстрочный символ показателя предшествующего (базисного) периода.

Индивидуальные индексы

Рассмотрим сначала индивидуальные индексы динамики. Индивидуальный индекс- относительный показатель изменения отдельного элемента сложного явления, например, его изменения в отчетном периоде по сравнению с базисным. Величина, изменения которой изучается , называется индексируемой (подстрочный индекс-1). Величина, с которой сравнивается индексируемая величина, называется базисной (подстрочный индекс-0). Рассмотрим наиболее распространенные в практике экономического анализа индивидуальные индексы.

Индивидуальный индекс цены рассчитывается по формуле:

,

где - индекс цены;

- цена товара в текущем периоде;

- цена товара в базисном периоде.

Индивидуальный индекс физического объема рассчитывается по формуле:

где - индекс физического объема ;

- количество товара, проданного в текущем периоде;

- количество товара, проданного в базисном периоде.

Индивидуальный индекс товарооборота рассчитывается по формуле:

,

где - индекс товарооборота;

- товарооборот в текущем периоде;

- товарооборот в базисном периоде.

Данные три индивидуальных индекса взаимосвязаны между собой:

,

то есть индекс товарооборота равен произведению индексов физического объема и цен, а изменение товарооборота складывается под воздействием динамики цены и изменения объема продажи данного товара.

Индивидуальные индексы, в сущности, представляют собой относительные показатели динамики или темпы роста и по данным за несколько периодов времени могут рассчитываться в цепной или базисной формах.

Сводные индексы. Агрегатная форма сводного индекса

Сводные индексы вычисляются по товарным группам и нескольким видам продукции. Сводные индексы могут быть представлены в трех формах: агрегатной, средней арифметической и средней гармонической.

Исходной и основной формой сводного индекса является агрегатная; средние индексы получаются в результате ее преобразования.В агрегатной формуле сводного индекса присутствуют два элемента:

Индексируемая величина, изменение которой показывает индекс (например, цена p);

Некоторая постоянная величин, называемая весом индекса (например q), с помощью которого несоизмеримые элементы сложного социально-экономического явления приводятся к сопоставимому виду. В числителе и знаменателе агрегатной формы находятся суммы произведений двух величин, одна из которых – индексируемая, другая постоянная (вес).

Различают индексы количественных и индексы качественных показателей. К количественным относятся показатели, харктеризующиефизические размеры явления (объемы продукции, численность работников, объем фондов и т.д.; при этом используются простые единицы измерения (метры, кг, штуки, руб.)).Качественный показатель используется для экономической (качественной) характеристики количественной единицы совокупности. Это цена за единицу товара, себестоимость едицы продукции, фондоотдача (единица измерения сложная – руб./ шт., руб./руб. и т. д.).

Индексы качественных показателей строятся с весами отчетного периода, а индексы количественных показателей строятся с весами базисного периода. Такое построения индексов позволяет получать систему взаимосвязанных индексов и проводить по ней анализ влияния отдельных факторов на изменение результативных показателей.

Рассмотрим агрегатный индекс товарооборота, показывающий изменение показателей разнородной продукции:

,

где n – число товаров, входящих в рассматриваемую группу.

В статистике принята упрощенная форма записи экономических индексов, без указания подстрочного (или надстрочного ) индекса номера товара, так как суммирование всегда осуществляется по всем товарам, входящим в товарную группу. К тому же по правилам векторной алгебры произведение векторов всегда равно сумме произведений соответствующих элементов векторов (в данном случае объемов и цен по каждой группе товаров) . При таком подходе формула сводного индекса принимает вид:

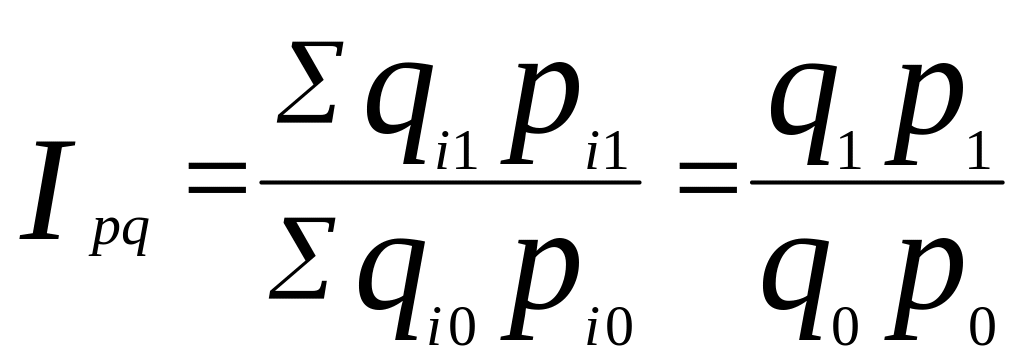, i = 1,2,3…n,

где - цена товара i-ой группы в текущем периоде;

- объем товара i-ой группы в текущем периоде;

- цена товара i-ой группы в базисном периоде;

- объем товара i-ой группы в базисном периоде;

- вектор цен товаров n групп в текущем периоде;

- вектор цен товаров n групп в базисном периоде;

- вектор объемов товаров n групп в текущем периоде;

- вектор объемов товаров n групп в базисном периоде;

- объем товарооборота (скалярная величина) по n группам в базисном периоде;

- объем товарооборота по n группам в текущем периоде.

На величину индекса товарооборота оказывают влияние как изменение цен, так и объемов продаж. Для того, чтобы оценить изменение только цен (индексируемой величины), необходимо количество проданных товаров (веса индекса) зафиксировать на каком-либо постоянном уровне. При исследовании динамики таких показателей, как цена, себестоимость, производительность труда, количественный показатель обычно фиксируют на уровне текущего периода. Таким способом получим простую формулу сводного индекса цен:

.

Аналогично рассчитывается сводный индекс физического объема продаж, только индексируемой величиной является количество товаров (записывается на первом месте), а весами выступают цены, фиксируемые на базисном уровне. Формула сводного индекса физического объема продаж имеет вид:

∑∑

Между сводными индексами цен, физического объема продаж и товарооборота существует взаимосвязь, которую можно использовать для проверки правильности расчетов:

Рассмотрим вычисление индексов на примере реализации мясных продуктов (табл.2.16.)

Таблица 2.16

Реализация мясных продуктов на рынке

Вид проду-кта, I		Октябрь					Ноябрь			Товарооборот
		Цена за кг, руб.,p0		Прода-но, т, q0		Цена за кг, руб., p1			Прода-но, т, q1	Тыс. руб. p0q0	Тыс. руб. p1q1	Тыс. руб. p0q1	Тыс. руб. p1q0
1	2		3		4			5		6	7	8	9
Говя-дина	80		2,8		90			2,5		224	225	200	252
Бара-ни-на	70		1,1		75			0,9		77	67,5	63	82,5
Свини-на	100		1,5		105			1,3		150	136,5	130	157,5
∑										451	429	393	492

Рассчитаем индексы:

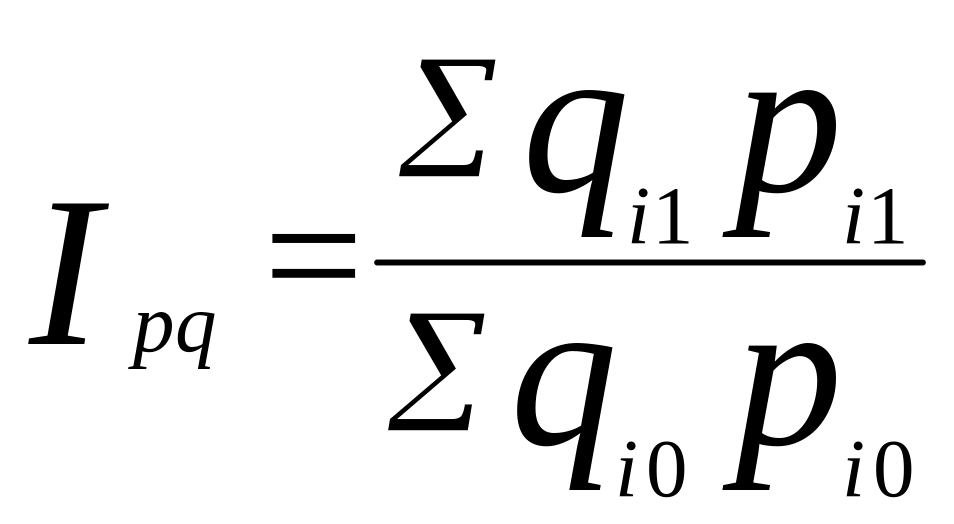= 429/451 = 0,951 (или 95, 1%);

Индекс товарооборота равен 0,951, то есть товарооборот сократился на 4.9 %.

Сокращение товарооборота Э = 429-451 = -22 тыс. руб.

= 429/ 393 = 1,092 ( или 109,2);

Индекс цен равен 1.092, то есть цены выросли на 9,2 %.

Потери покупателей от роста цен Э= 429 – 393 = 36 тыс.руб.

= 429/492 = 0,871 (или 87, 1);

Индекс физического объема равен 0, 871, то есть объем продаж сократился на 12, 9 %. Потери продавцов от сокращения объема продаж Э= 429 – 492 = 63 тыс.руб.

Проверим правильность расчетов индексов, используя их взаимосвязь:

I_pI_q = I_pq = 1,092*0,871 = 0,951.

При анализе результатов производственной деятельности эти же сводные индексы называют соответственно индексом стоимости продукции ( ), индексом оптовых цен ( ) и индексом физического объема продукции в натуральном выражении ( ).

Для определения общего изменения уровня себестоимости нескольких видов продукции, выпускаемых предприятием, рассчитывается сводный индекс себестоимости:

,

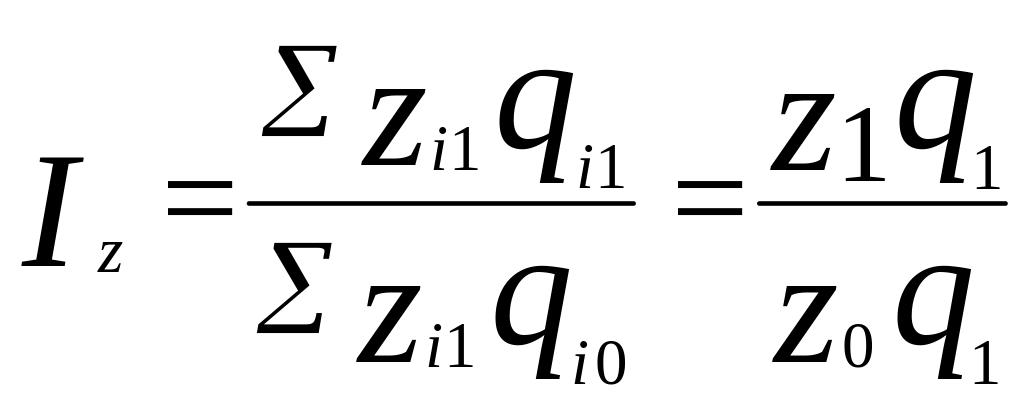где z₁ - вектор себестоимости продукции n групп в текущем периоде;

z₀ - вектор себестоимости продукции n групп в базисном периоде;

- сводный индекс себестоимости продукции.

Числитель этого индекса отражает затраты на производство текущего периода, а знаменатель условную величину затрат при сохранении себестоимости на базисном уровне. Разность числителя и знаменателя показывает сумму экономии предприятия от снижения себестоимости (Э):

Э = z₁q₁ – z₀q₁.

Cводный индекс физического объема продукции, взвешенный по себестоимости продукции (I_q), имеет следующий вид:

.

Третьим показателем в этой индексной системе эатрат является сводный индекс затрат на производство (I_zq):

.

Все три индекса взаимосвязаны между собой:

I_zq = I_zI_q.

Индексный метод также широко используется в анализе производительности труда.Возможны два подхода к расчету таких индексов (на основе учета количества продукции, выработанной в единицу времени w, и на основе учета затрат рабочего времени на единицу продукции t. Количество продукции, вырабатываемое в единицу времени (в натуральном выражении), и затраты времени на единицу продукции взаимосвязаны между собой :

.

Основанные на показателях выработки и трудоемкости индивидуальные индексы имеют следующий вид:

;

,

где T- суммарные затраты времени на выпуск данной продукции в человеко-часах, человеко-днях или человеко-месяцев (в последнем случае соответствует общей численности работников).

При расчете сводного индекса производительности труда в стоимостном выражении (по выработке) необходимо количество продукции, произведенной за каждый период, взвесить по каким-либо ценам, принятым за сопоставимые. Такой сводный индекс производительности труда (по выработке) рассчитывается по формуле:

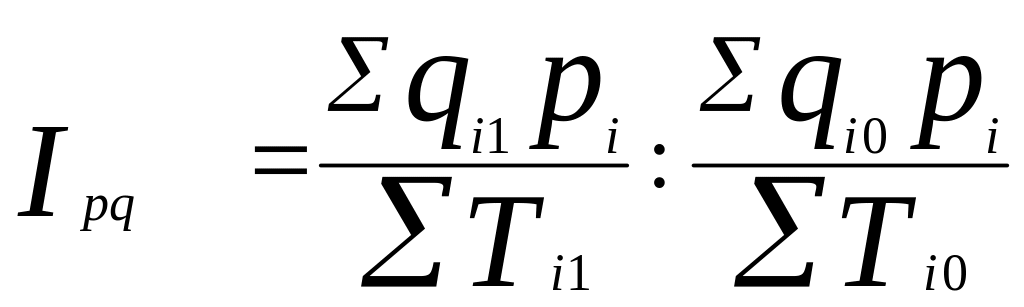
Первая часть представляет собой среднюю выработку в отчетном периоде,вторая –в базисном.

Произведение индекса производительности труда по выработке и индекса затрат рабочего времени приводит к индексу физического объема продукции, взвешенного по цене:

или

.

Сводный индекс производительности труда (по трудоемкости) рассчитывается по данным о трудоемкости различных видов продукции и объемах их производства:

,

где t₀ - вектор трудоемкости продукции в базисном периоде;

t₁- вектор трудоемкости продукции в текущем периоде;

q₁- вектор объемов производства продукции в текущем периоде.

I_t – сводный индекс производительности труда (по трудоемкости).

Знаменатель этого индекса отражает реально имевшие место общие затраты времени на выпуск всей продукции в текущем периоде (T₁). Числитель представляет собой условную величину, показывающую, какими бы были затраты времени на выпуск этой продукции, если бы трудоемкость не изменилась.

Индекс производительности труда связан с индексом затрат рабочего времени (труда) и с индексом физического объема, взвешенным по трудоемкости:

или

Индексные системы в динамике

Если индексы рассчитываются за ряд последовательных периодов, то веса могут быть постоянными или переменными, цепными или базисными. Рассмотрим некоторые варианты построения индекса цен за m периодов.

1. Цепные индексы цен с переменными весами:

или

2. Цепные индексы с постоянными весами:

Веса могут фиксироваться на уровне базисного периода (как в примере) по методу Ласпейреса и на уровне последнего года по методу Пааше.

3.Базисные индексы с переменными весами:

Индексы характеризуют изменение цен в текущем периоде по сравнению с неизменным базисным уровнем ( в исследовании помесячной динамики в качестве такого уровня обычно принимается декабрь предшествующего года).

4.Базисные индексы с постоянными весами:

Отличие данной индексной системы от предшествующей заключается в том , что здесь не меняется не только база сравнения, но и веса. Использование базисных весов позволяет исключить влияние структурных изменений в объемах продаж на сводные индексы.

Выбор той или иной системы индексов зависит от целей исследований и имеющейся информации. Определенные преимущества имеет второй вариант системы (цепные индексы с постоянными весами), так как в ней индексы мультипликативны- их последовательное перемножение позволяет получить базисный индекс в целом за исследуемый временной интервал.

Средние формы сводных индексов

Сводные индексы могут быть получены путем осреднения индексов индивидуальных, то есть рассчитаны как средневзвешенная величина из индивидуальных индексов. В зависимости от вида весов (базисные (по методу Ласпейреса) или текущие (по методу Пааше)) различают среднеарифметический и среднегармонический индекс. При расчете среднеарифметического индекса производится замена :

, или

где i_рi -индивидуальный индекс цен i-го товара;

i_p - вектор индивидуальных индексов цен товаров.

И формула среднего индекса цен будет иметь вид:

где ( )- вектор товарооборота (объема продаж в стоимостном выражении) в базисном периоде.

При расчете среднегармонического индекса производится замена :

, или ,

, или

И формула среднегармонического индекса цен будет иметь вид:

,

где - вектор обратных величин индивидуальных индексов цен товаров;

- вектор товарооборота (объема продаж в стоимостном выражении) в отчетном периоде.

Индексный анализ факторов изменения среднего уровня

Рассмотрим случай, когда один товар реализуется в нескольких местах или один вид продукции производится на ряде предприятий.Для этого случая можно рассчитать среднюю цену в каждом временном периоде. По отношению этих средних можно получить три взаимосвязанных индекса: индекс переменного состава, индекс структурных сдвигов и индекс фиксированного состава.

Индекс переменного состава определяется по формуле:

,

Индекс фиксированного о состава определяется по формуле:

.

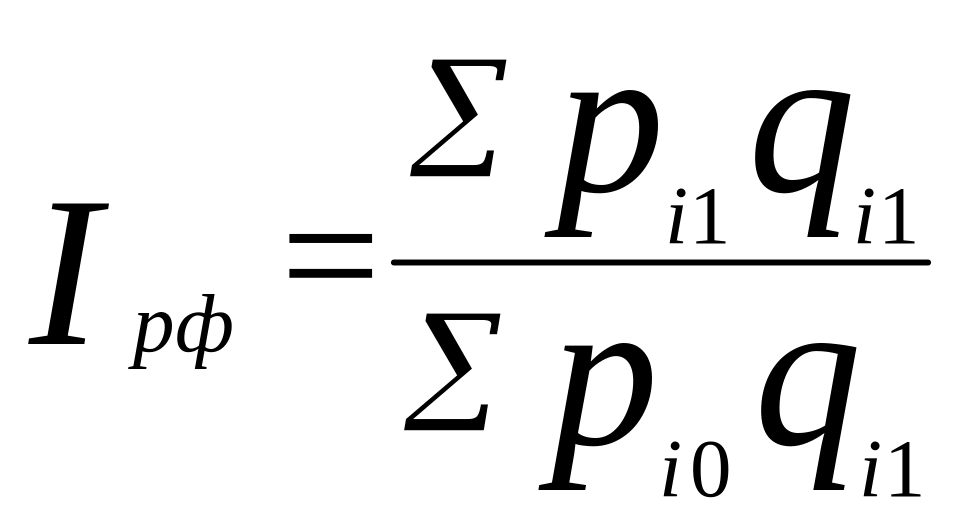Индекс структурных сдвиго определяется по формуле:

.

Первая часть индекса позволяет определить среднюю цену текущего периода при условии, если бы цены остались на уровне базисного периода. Вторая часть отражает среднюю фактическую цену базисного периода. В целом по индексу можно судить об изменении цены за счет структурных сдвигов. Взаимосвязь индексов следующая:

,

То есть индекс переменного состава равен произведению индекса фиксированного состава на индекс структурных сдвигов. Аналогично строятся и используются индексы для анализа изменения себестоимости, урожайности и других показателей.

Использование индексов в территориальных сравнениях

В отличие от динамических территориальные индексы служат для сравнения показателей в пространстае, то есть по предприятиям, округам, городам, районам и т.п. Построение территориальных индексов требует решения вопросов, связанных с выбором базы сравнения и весов, или уровня, на котором фиксируются веса.

При двусторонних сравнениях каждая территория может быть и сравниваемой (числитель индекса, и базой сравнения. Веса как первой , так и второй территории, также имеют равные основания для использования при расчетах.Чтобы не было неопределенности, в качестве весов принимаются объемы проданных товаров по двум регионам (А и B), вместе взятым:

Q = q_a +q_b .

Территориальный индекс в этом случае рассчитывается по формуле:

.

Можно рассчитать и обратный индекс:

.

Второй способ расчета территориальных индексов заключается в учете соотношения весовна каждой из территорий.Для этого сначала определяется средняя цена каждого товара по территориям, вместе взятым:

.

После этого рассчитывается территориальный индекс по формуле:

.

Разложение абсолютных приростов по факторам

Построение взаимосвязанных индексов позволяет одновременно решать две задачи : определить изменение сложного (результативного) показателя в относительном и абсолютном выражении за счет влияния отдельных факторов. Расчет изменения результативного показателя за счет изменения отдельных факторов в абсолютном выражении называется разложением абсолютного прироста (убыли) по факторам.

Рассмотрим методы разложения по факторам на примере двухфакторной модели. Пусть имеются данные по сельскохозяйственному предприятию о продаже картофеля на трех рынках области (табл.2.17, графы А, 1-4). Требуется определить абсолютное и относительное изменение выручки от продажи картофеля в апреле по сравнению с выручкой в марте и разложить абсолютное изменение по факторам.

Общая выручка равна сумме произведений цены на объем продаж (∑p₀q₀ -за март- 17800 руб., ∑ p₁q₁ –за апрель- 29400 руб., графы 5, 6 табл. 1.1) и относительное изменение выручки от продажи

равно:

Таблица 2.17

Данные о продаже картофеля на трех рынках

Ры-нок	Цена 1 кг. руб.			Продано Кг		Выручка от продажи, руб.		p0q1
	Март p0	Ап-рель p1	март q0		Ап-рель q1	март p0q0	Апрель p1q1
A	1	2	3		4	5	6	7
1	8	10	800		1000	6400	10000	8000
2	9	12	600		800	5400	9000	7200
3	10	14	600		700	6000	9800	7000
∑	-	-	2000		2500	17800	29400	22200

= 1, 651 ( или 165,1 %).

В абсолютном выражении изменение выручки составило:

∆pq = ∑ p₁q₁ - ∑ p₀q₀ = 29400 – 17800 = 11600 руб.

Так как общая выручка зависит от объема продаж в натуре и от цен, рассчитаем соответствующие индексы.

= 1, 247 ( или 124,7 %);

( или 132,4%).

Это означает, что общая выручка от продажи картофеля выросла на 24, 7 % за счет изменения количества реализованной продукции и на 32,4 % за счет изменения цен. Причем рост выручки вызван не только изменением общего количества проданного картофеля, но и доли реализации на отдельных рынках, то есть изменением структуры продаж.

В целом относительное изменение стоимости равно произведению факторных индексов, то есть агрегатные индексы результативного и факторных показателей связаны мультипликативно:

I_pq = I_pI_q

или = 1,324. 1,247 = 1,651.

Соответственно абсолютный прирост можно разложить по факторам по следующем схеме (первый метод):

или

∆pq = _p∆pq + _q∆pq,

где ∆pq = - общее изменение выручки;

_p∆pq = - изменение выручки за счет изменения цен;

_q∆pq = - изменение выручки за счет изменения объема и доли( структуры) продаж.

Так , в нашем примере ∆pq =11600 руб., _p∆pq =29400 – 22200 = 7200 руб., _q∆pq = 22200-17800 = 4400 руб. В целом, 11600 = 7200 + 4400.

Такой метод наиболее распространен, но при таком разложении структурный фактор остается невыделенным.

Второй метод разложения по факторам применим к однородным совокупностям, для которых можно рассчитать средние значения индексируемого качественного показателя и индексы переменного и фиксированного состава и структурных сдвигов. По данным того же примера (табл. 1.1.) для каждого месяца рассчитаем среднюю цену на картофель, а именно:

в марте = 17800/2000 = 8,9 руб.;

в апреле = 294400/2500 = 11,76 руб.

Сопоставляя средние цены на картофель за два меcяца, получим индекс переменного состава:

= 11,76/8,9 = 1,321 (или 132,1 %),

который показывает, что средняя цена на картофель в апреле по сравнению со средней ценой в марте возросла на 32,1 %. Цена изменилась и за счет изменения цен на отдельных рынках и за счет изменения структуры продаж на них. Чтобы устранить влияние структурного фактора рассчитаем индекс фиксированного состава:

= 29400/22200 = 1,324 ( или 132,4 %).

Значение этого индекса совпадает с индексом физического объема I_p по первому методу.

Разделив индекс цен переменного состава на индекс фиксированного состава, получим индекс структурных сдвигов, характеризующий изменение средней цены за счет изменения доли продаж на отдельных рынках.

= 1,321 /1,324 = 0,998 (или 99,8 %).

Этот же результат можно получить непосредственно по формуле :

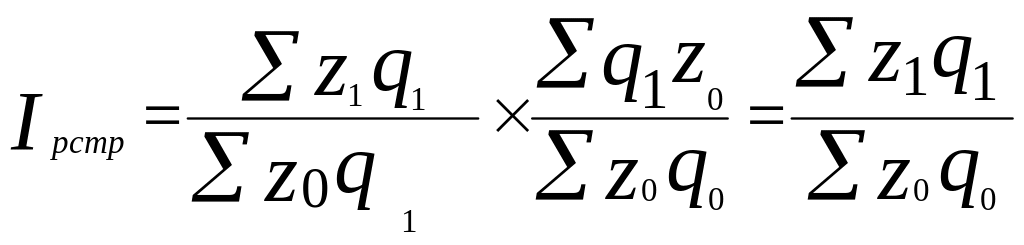= 8,88: 8,9 = 0,998.

То есть, на 0,2 % средняя цена снизилась за счет изменения структуры продаж.

Следовательно, абсолютный прирост выручки ∆pq =11600 руб. можно разложить по факторам:

1. за счет изменения общего объема проданного картофеля :

_∑p∆pq= (∑q₁ - ∑q₀). = (2500-2000).8,9 = 4450 руб.

2. За счет изменения средней цены на картофель

_pср∆pq = = (11,76 -8,9)2500 = 7150 руб.

Этот результат можно разложить на 2 слагаемых:

а) прирост выручки за счет изменения цен на отдельных рынках:

_p∆pq = = 29400- 22200 = 7200 руб.;

б)прирост выручки за счет изменения структуры

_qср∆pq = ∑q₁= (8,88-8,9)2500 = - 50 руб.

В сумме 7200 и (-50) дают 7150.

Таким образом, мы разложили общий абсолютный прирост, равный 11600 руб. , на 3 части:

1. 4450 руб. – за счет изменения объема реализации картофеля;

2. 7200руб. – за счет изменения цен на картофель (на всех рынках);

3. -50 руб.- за счет структурного фактора.

Аналогично проводится анализ изменения затрат на производство продукции под воздействием двух факторов: изменения себестоимости продукции и объемов производства. Относительное влияние отражают индексы:

I_zq = I_zI_q = .

Абсолютное изменение затрат на производство за счет отдельных факторов рассчитывается следующим образом:

∆zq = ∑z₁q₁ -∑z₀q₀;

∆zq_z =∑z₁q₁ -∑z₀q₁;

∆zq_q = ∑ q₁z₀ -∑ q₀z₀.

Взаимосвязь абсолютных изменений определяется уравнением:

∆zq = ∆zq_z + ∆zq_q.

Методы расчета и анализа индексов цен

В статистическом изучении динамики цен ведущая роль принадлежит индексному методу. Сравнение цен одного товара осуществляется с помощью индивидуального (однотоварного) индекса цен:

где pⁱ₀ , pⁱ₁ – цены на товар в базисном и текущем периоде.

Индекс средних цен применяется при изучении изменения цен товарных групп, цен одного товара по различным территориям и субрынкам:

Где p_i1, q_i1- цена и количество проданного i - го вида товара (товара на i - й территории или i - м субрынке) в отчетном году, i = l,…, n;

p_i0, q_i0 - цена и количество проданного i - го вида товара (товара на i - й территории или i - м субрынке) в базисном году, i=l,…, n.

Товары должны быть достаточно однородными, чтобы их количество поддавалось суммированию.

Основной формой индекса цен для совокупности разнородных товаров является агрегатный индекс. Цены различных товаров (например, кондитерских изделий и компьютеров) складывать бессмысленно. Несуммируемость элементов совокупности преодолевается путем взвешивания каждой цены по количеству проданных товаров. Сумма произведений цен товаров на их количество составляет товарооборот совокупности товаров. Чтобы выявить непосредственно изменение цен, необходимо зафиксировать показатели количества на одном из уровней:

– базисного периода времени (формула Ласпейреса);

, где q₀ – количество товара в базисном периоде, p₁ и p₀ – цена единицы товара соответственно в отчетном и базисном периодах

- текущего периода времени (формула Пааше)

, где q₁ – количество товара в отчетном периоде.

Четкость интерпретации, экономический смысл и удобство практического расчета формулы Ласпейреса сделали ее самой популярной в мире для расчета индекса потребительских цен, который показывает, во сколько раз изменились бы потребительские расходы в текущем периоде по сравнению с базисным, если бы при изменении цен уровень потребления оставался прежним. Такой расчет корректен при отсутствии значительных количественных и качественных изменений в структуре потребления (во времени и по территории, если индекс рассчитывается для нескольких регионов).

Изучение динамики розничных цен (например, для получения дефлятора, позволяющего рассчитать стоимостные показатели от четного периода в сопоставимых ценах) должно быть максимально приближено к совокупности товаров, произведенных в отчетном периоде. Результат расчета по формуле Пааше показывает, во сколько раз сумма фактических затрат населения на покупку товаров больше (меньше) суммы денег, которую население должно было бы заплатить за эти же товары, если бы цены оставались на уровне базисного периода. Статистическим анализом доказано, что в долговременном аспекте формула Пааше занижает реальное изменение цен вследствие общественной отрицательной корреляции (относительный вес товара падает, если цена его возрастает).

Доказано, что наилучший линейный индекс лежит между индексами, вычисленными по формулам Ласпейреса и Пааше. Зарубежные статистики пытались найти компромиссную формулу.

Формула Эджворта - Маршалла:

I_Э-М= (pⁱ₁((q₁+q₀)/2))/(pⁱ₀((q₁+q₀)/2))

Эта формула улавливает сдвиги в структуре покупок, но привязана к условной структуре товарооборота, не характерной ни для одного реального периода, не имеет прямого экономического смысла. Ее расчет встречает препятствия в сборе материалов.

Наиболее удачным компромиссом многие экономисты считают «идеальный» индекс Фишера:

который оценивает не только набор товаров базисного периода по ценам текущего, но и набор товаров текущего периода по ценам базисного. Применяется в случае трудностей с выбором весов или значительного изменения структуры весов.

Разновидностью розничных цен являются цены на продукты массового (общественного) питания. Они образуются на базе розничных или оптовых цен на продукты, покупаемые предприятиями массового питания с добавлением наценки, возмещающей издержки на переработку продуктов и дающей прибыль. Непосредственная регистрация цен продукции массового питания практически невозможна из-за большого разнообразия ее состава и отсутствия стабильной единицы измерения. Поэтому для расчета индекса цен на продукцию массового питания исчисляют индекс цен на израсходованные продукты и товары, проданные на предприятиях массового питания, и индекс ценовых факторов наценки (Inp). Последний, в свою очередь, состоит из двух индексов: индекса норм наценок (т. е. процента наценки к цене продукта) и индекса изменения самих цен:

где n₁,p₁,q₁– норма наценки, цена и количество товаров в отчетном году; n₀, p₀, q₀ - норма наценки, цена и количество товаров в базисном году; k – число i-x разновидностей товаров;

Так как расход продуктов в производстве продукции массового питания учитывается в стоимостных единицах, то для расчета используется формула среднего гармонического индекса:

где

Формула индекса цен массового питания имеет вид:

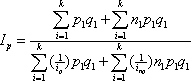
Индексы при систематическом расчете из года в год образуют индексные ряды. Различают базисные ряды (цены каждого года сравниваются с ценами года, принятого за базу) и цепные (характеризующие изменение цен по сравнению с предыдущим годом). Веса индексов ряда могут быть постоянными (на уровне одного года), и тогда произведение цепных индексов даст базисный индекс.

Применение системы переменных весов (по количеству товаров отчетного года) в индексном ряду цен порождает ошибку при переходе от цепных индексов к базисным и обратно, так как позитивна корреляция между текущим изменением цен и прошлым изменением количества проданных товаров. Эта ошибка мала, если корреляционная связь между изменением цен и количества проданного товара незначительна. На практике система цепных индексов (достоинство - сокращает период сравнения, ограничивает круг несопоставимых товаров) используется для коротких периодов, затем осуществляется поправка по формуле базисного периода, так как за длительный период ошибка накапливается.

Численные значения индексов, рассчитанных по различным формулам на основе одних и тех же данных, отличаются и порой значительно, особенно в годы резких изменений уровня цен и связанного с этим изменения структуры спроса. Отдать предпочтение одной формуле трудно: разные цели диктуют применение индексных форм, имеющих разный экономический смысл. Отказ от концепции единственного индекса цен в пользу концепции системы индексов позволит дать обобщающую характеристику и оценку основных причин изменения розничных цен. Но поскольку все же индексный метод не универсален, а отражает лишь тенденцию движения цен, то нельзя требовать большей определенности от рассчитанных индексов. Кроме того, на чистоту результатов огромное влияние оказывает достоверность исходных материалов, особенно ошибка выборки, степень представительности товаров, включенных в расчет.

Методы оценки уровня и динамики инфляции

Одной из самых важных характеристик состояния экономики любой страны является уровень инфляции, который проявляется в росте общего уровня цен. Рост уровня цен неравнозначен понятию «инфляционный рост цен», так как может включать изменение цен, обусловленное изменением качества продукции и услуг. Не существует единого статистического показателя, способного отделить один из другого, тем более что оценка изменения качества не возможна без привлечения экспертных методов. Поэтому адекватная оценка инфляции возможна только с использованием развернутой системы показателей.

Для наиболее общей характеристики уровня инфляции в мировой практике используются два показателя. Индекс потребительских цен (ИПЦ) позволяет оценить уровень инфляции на потребительском рынке.

Дефлятор валового внутреннего продукта (ДВВП) оценивает степень инфляции по всей совокупности благ, производимых и потребляемых в государстве, учитывает не только изменение цен товаров народного потребления, но и цен товаров, используемых в государственных интересах, инвестиционных, экспортируемых и импортируемых товаров и услуг. В большинстве стран ИПЦ публикуется ежемесячно, в кризисных условиях - еженедельно. Периодичность расчета ДВВП квартальная или годовая. Это связано с относительной сложностью его расчета.

В России ИПЦ исчисляется за каждый месяц и нарастающим итогом с начала года по модифицированной формуле Ласпейреса:

где pⁱ_t-1qⁱ₀ = p₀q₀ (p₁/p₀)(p₂/p₁)(…)(p_t/p_t-1).

Модификация состоит в том, что изменение цен исчисляется на основе последовательных наблюдений цены, т. е. в каждый период времени базовые веса умножаются на последнее значение индекса цен.

ДВВП в большинстве стран определяется по методу Пааше. Известная формула может быть представлена в виде:

где p_tq_t – номинальный ВВП, p₀q_t – реальный ВВП.

Отечественная практика расчета ДВВП имеет некоторые особенности: сначала с помощью индексов цен или физического объема (в зависимости от имеющейся базы) производится постатейная переоценка ВВП, рассчитанного по методу конечного использования, в ценах предыдущего года. Затем по формуле Пааше рассчитывается цепной ДВВП. Базисный ДВВП определяется путем перемножения всех годовых ДВВП в промежутке от отчетного до - базисного года.

Основным показателем динамики инфляции служит норма инфляции:

N=(I_t - I_t-1) /I_t где I_t и I_t-1 – индексы цен смежных периодов.

Норма инфляции показывает, на сколько процентов изменился уровень инфляции за данный период времени. Если N составляет 1 – 9 %, инфляция называется «ползучей», 10 – 49 % - «галопирующей». В случае 50 % и более в месяц - экономика «больна» гиперинфляцией.

Для измерения инфляции используется индекс покупательной способности денежной единицы, показывающей, во сколько раз обесценились деньги:

I_П.С.= 1 / I_p

Одной из составляющих инфляции является денежная масса, не обеспеченная соответствующим количеством товаров и услуг. Величина денежной массы зависит от количества денег в обращении и от скорости их обращения. Теоретически относительный рост денежной массы при замедлении оборота денег может не привести к инфляции, например, если повышены процентные ставки на депозиты. Но, как правило, не обеспеченный товарами выпуск денег побуждает покупателей к быстрой их реализации, что увеличивает скорость оборота денег и усиливает разбег инфляции. Величина товарной массы, второй составляющей инфляции, зависит от ее физического объема и цен товаров. Поскольку товарная и денежная масса стремятся к рыночному равновесию, то рост средних цен товарной массы определяется размером изменения ее физического объема, массы денег в обращении и скорости их обращения. Таким образом, общий размер инфляции прямо пропорционален росту денежной массы и увеличению скорости обращения денег и обратно пропорционален росту товарной массы (в постоянных ценах).

Денежная масса рассчитывается государственной статистикой как оборот и остатки наличных и безналичных денежных средств, сумма всех доходов с учетом размера накоплений, взносов и платежей; товарная масса - как товарооборот и продажа услуг, денежные расходы населения на покупку товаров и услуг или ВВП.

Степень соответствия товарной и денежной массы оценивается с помощью ряда показателей: - соотношения денежной и товарной массы в статистике и динамике;

- соотношения темпов роста денежной эмиссии и цен;

- соотношения темпов роста доходов и цен.

Изменение номинальных доходов (p₁q₁-p₀q₀) складывается из изменения реальных (пересчитанных в сопоставимые цены) доходов (p₀q₁-p₀q₀) и роста доходов за счет изменения цен (p₁q₁-p₀q₁).

Сопоставление этих показателей покажет размер потерь (прироста) реальных доходов, или насколько рост доходов населения возмещал его потери от обесценения денег. Аналогично осуществляется анализ реальных потерь денежных накоплений населения.

В качестве информационной базы для анализа инфляции используются различные источники. Цены на товары и услуги-представители собираются статистикой методом выборочного наблюдения; структура потребительских расходов определяется статистикой семейных бюджетов в ходе регулярных обследований; система статистической отчетности получает данные о товарообороте; сведения о денежной массе статистические органы получают от банков; баланс денежных доходов и расходов населения позволяет определять затраты на приобретение товаров и услуг.

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1. Какова роль индексного метода анализа в экономических исследованиях?

2. На каких принципах базируется расчет агрегатных индексов объемных и качественных показателей?

3. В чем различие агрегатных индексов Ласпейреса и Пааше и какие факторы оказывают влияние на расхождение в величине этих индексов?

4. Какие виды средних индексов используются в статистической практике и для решения каких проблем?

5. Запишите формулу «идеального» индекса Фишера. Какой вид средних величин используют для его расчета?

6. Что характеризует индекс влияния структурных сдвигов? Напишите формулу для его расчета.

7. Какие методические приемы используют при расчете индексов фондового рынка?

8. Как измерить уровень инфляции?

9. Какие формы индексов используют при территориальных сопоставлениях?

10. Какие характеристики определяют вид расчетной формулы фондового индекса?

ТЕСТЫ

1. По составу явления различают индексы:

1) агрегатные и средние из индивидуальных;

2) динамические и территориальные;

3) индивидуальные и общие;