Условия окончания итерационного процесса.

Процесс итераций заканчивается при одновременном выполнении двух условий:

1. Если два последующих приближения отличаются между собой по модулю на величину, не превышающую заданной точности , т.е. . Отдельно этого критерия недостаточно, так как в случае крутизны графика, данное условие будет выполнено, но может находиться далеко от корня.

2. Мера удовлетворения уравнению (2.1) последнего приближения корня: 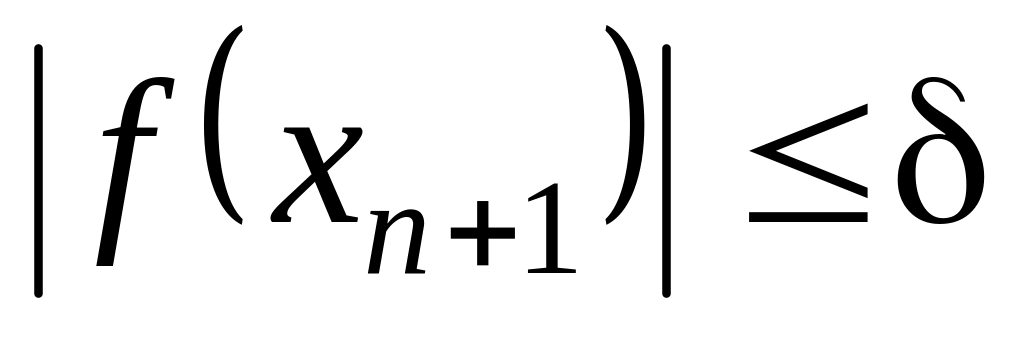. Отдельно данного критерия недостаточно, так как при пологой функции это условие может быть выполнено, но может находиться далеко от корня.

Метод простых итераций имеет два достоинства:

- является универсальным, простым для реализации на ЭВМ и самоисправляющимся, то есть любая неточность на каком – либо шаге итераций не отразится на конечном результате, а отразится лишь на количестве итераций. Подобные ошибки устойчивы даже по отношению к грубым ошибкам (сбоям ЭВМ), если только ошибка не выбрасывает очередное приближение за пределы области сходимости.

- позволяет достигнуть любой заданной точности при любом начальном приближении .

Недостатки метода:

- трудоемкость процесса приведения уравнения (2.1) к виду (2.4).

- если начальное приближение выбрано достаточно далеко от корня, то число итераций, необходимых для достижения заданной точности, будет достаточно большое и объем вычислений возрастет.

Пример 2.4. Доказать графическим и аналитическим методами существование единственного корня нелинейного уравнения

(2.14)

на отрезке и построить рабочие формулы метода простых итераций для поиска корня.

1. Докажем графическим методом единственность корня нелинейного уравнения (2.14). Из графика функции на рисунке 2.8 видно, что функция пересекает ось в одной точке, являющейся приближенным значением корня нелинейного уравнения (2.14). Но так как данная функция имеет сложный аналитический вид, то преобразуем уравнение (2.14) к виду и построим два графика и , имеющих более простой аналитический вид (Рис.2.9). Абсцисса точки пересечения графиков является приближенным значением корня.

Д ля доказательства единственности корня на отрезке воспользуемся аналитическим методом. Функция непрерывна на отрезке , имеет на концах отрезка разные знаки ( ), а производная функции не меняет знак на отрезке ( ). Следовательно, нелинейное уравнение (2.14) имеет на указанном отрезке единственный корень.

2. Для построения рабочей формулы перепишем уравнение (2.14) в виде: . Проверим, выполняется ли достаточное условие сходимости (2.6). Заметим, что в точке из отрезка , значение , т.е. условие не выполняется. Построим функцию . Так как всюду положительна на отрезке, то, конкретизируя значение производной в любой точке отрезка в неравенстве , значение определяется из интервала . Выбрав значение , запишем рабочую формулу метода простых итераций:

(2.15)

Итерационный процесс (2.15) можно начать, задав произвольное начальное приближение .