6. Нормальное распределение гаусса

В практике измерений чаще всего реализуется так называемый нормальный закон распределения случайных величин - нормальное распределение Гаусса. В частности, всевозможные измерения (длины, диаметра, массы, напряжения, плотности, объема), с которыми приходится наиболее часто сталкиваться, имеют распределения, близкие к нормальному.

Причина широкого распространения нормального распределения связана с тем, что на результаты физических измерений влияет очень много факторов (температура, влажность, колебания прибора, движение воздушных потоков, солнечная активность, наличие загрязнений), которые не поддаются точному анализу. Каждый из этих факторов порождает элементарную погрешность измерения. Поскольку число этих факторов велико, их совокупное действие порождает уже заметную “суммарную погрешность”.

Существует так называемая центральная предельная теорема, которая гласит, что если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.

Рассматривая суммарную погрешность как сумму очень большого числа взаимно независимых частных погрешностей, заключаем, что значения отсчетов имеют распределение, близкое к нормальному.

Плотность вероятности нормального распределения задается математической функцией вида

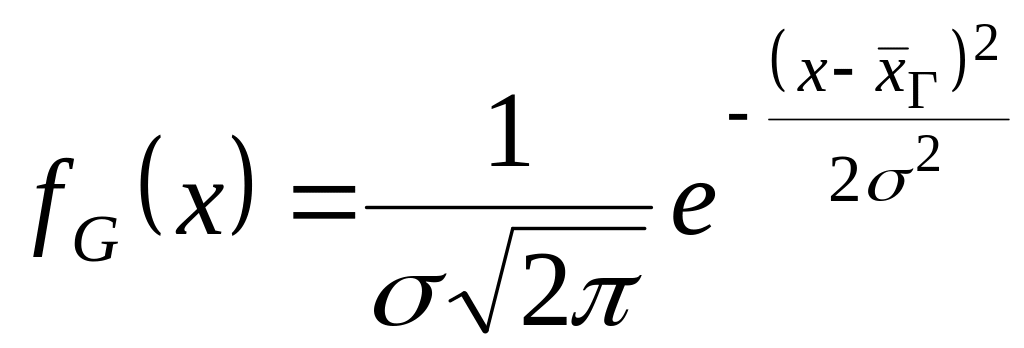
, (6)

где - отклонение случайной величины x от истинного (генерального среднего) значения и e=2,718.

В формулу (6) входят два параметра -  и . Параметр  совпадает с генеральной дисперсией. При функция имеет максимум. Это означает, что значения x, лежащие около истинного значения величины, получаются при измерениях с наибольшей вероятностью.

На рисунки представлены графики нормальной кривой для различных значений . На графике видно, что чем больше значение , тем шире кривая распределения, т.е. чаще при прочих равных условиях встречаются большие отклонения _x. Оба графика имеют максимум в случае отклонения _x=0. Кривые симметричны относительно оси ординат, проходящей через точку ; отклонения равной величины, но разного знака равновероятны.

С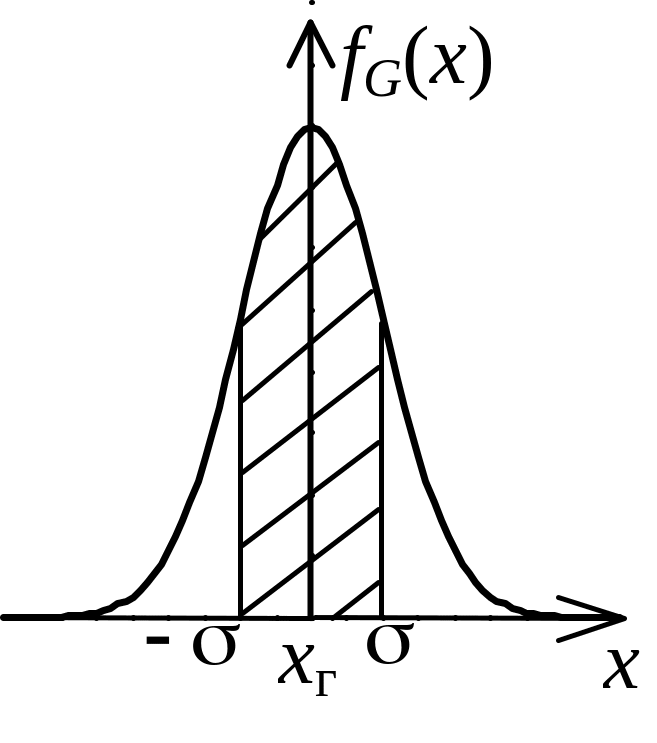 мысл функции плотности распределения заключается в том, что площадь фигуры, заключенной между кривой, осью x и двумя ординатами из точек x₁, и x₂ (заштрихованная площадь на рисунке), численно равна вероятности, с которой любой отсчет попадает в интервал [x₁, x₂]. Очевидно, вся площадь под любой кривой (с любым значением ) равна точно единице.

На кривой нормального распределения абсциссы точек, равные  соответствуют местам, где выпуклость кривой переходит в ее вогнутость. Заштрихованная площадь равна 0,68 всей площади, находящейся под кривой Гаусса. Другими словами, значения и являются границами интервала, за пределы которых с вероятностью 0.68 не выйдет отклонение _x.

Принимают, что значения отсчетов всегда лежат в пределах от до . Полученный вывод называется правилом трех сигм.

К ак указывалось разброс значений выборочных средних около истинного значения измеряется величиной , т.е. с увеличением числа отсчетов n ошибка выборочного исследования уменьшается. Это свойство не зависит от вида распределения генеральной совокупности. Если генеральная совокупность распределена нормально, распределение выборочных средних также будет нормальным независимо от объема выборки. При этом кривая распределения выборочных средних более сжата, чем кривая распределения отсчетов, что соответствует меньшему разбросу выборочных средних вокруг истинного значения

Положительной стороной метода статистического усреднения является то, что при усреднении одновременно уменьшаются все случайные погрешности независимо от их происхождения. При этом соотношение справедливо при любом законе распределения исходных данных и любом их числе (при условии независимости измерений).