4. Сбалансированные деревья. Основные определения и операции.

Количество сравнений при поиске по бинарному дереву поиска колеблется от до n/2 в худшем. Хотелось бы иметь алгоритм эффективного поиска, вставки и удаления элементов, который сохранял бы дерево в некотором сбалансированном состоянии.

Глубина бинарного дерева – максимальный уровень его листьев.

Баланс некоторого узла – высота его левого поддерева минус высота его правого поддерева.

Сбалансированное бинарное дерево – у которого абсолютное значение баланса каждого узла меньше или равно 1 (допустимый баланс (-1), 0, 1).

Дано некоторое сбалансированное дерево. Необходимо добавить новый элемент. В результате дерево либо сбалансированное, либо не сбалансированное (если вставляемый узел является левым потомком некоторого узла, которое ранее имело баланс =1, либо правым потомком некоторого узла, баланс которого был =(-1)). Если после включения элемента баланс был нарушен, нужно найти самый нижний разбалансированный узел.

Повороты.

Алгоритм «Левый поворот».

1. Work2=Work1→PRP

2. Work1→PRP= Work2→PLP

3. Work2→PLP= Work1

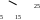
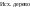
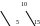
П 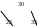ри любом повороте значение указателя на корень поддерева так же должно изменяться, чтобы указывать на новый корень (указатель Work2). При любом из поворотов дерево остается бинарным деревом поиска. Следовательно для получения сбалансированного дерева можно выполнять любое число левых или правых поворотов.

При левом повороте: указатель Work1(вершина 20), Work2 (вершина 30) .

Р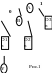 ассмотрим поддерево, имеющее корень в самом младшем предке, которое стал не сбалансированным в результате добавления некоторого узла. Пусть баланс поддерева до добавления был равен 1 (для (-1) тот же алгоритм, все симметрично.)

Узел А – не сбалансированный узел. Т.к. баланс этого узла был =1, то его левое поддерево не пусто. Узел В - левый потомок. Т.к. узел А является самым младшим предком, который стал не сбалансированным, то узел В должен иметь баланс =0. Узел В должен иметь до вставки левое и правое поддеревья равной высоты n (возможно поддеревья пустые).Т.к. баланс узла А был равен 1, то правое поддерево A(D3) имеет высоту n.

Рассмотрим два случая.

С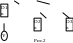 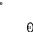лучай 1. Добавляемый узел вставляем в левое поддерево узла В(рис.1), изменяя баланс узла В на 1, а узла А на 2. Для дерева на рис.1 выполним правый поворот. Дерево на рис.2 –дерево бинарного поиска, сбалансированное.

С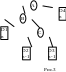 лучай 2. Дерево на рис.1. Добавляемый узел вставляем в правое поддерево узла В. Пусть узел С будет потомком узла В. Имеется 3 варианта: узел С является вставляемым узлом (тогда у него левое и правое поддерево пустое); когда добавляемый узел включается в левое или правое поддерево узла С.

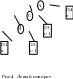
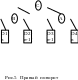
Д ля балансировки дерева на рис.3 необходимы 2 поворота: левый поворот поддерева с корнем в узле В и правый поворот поддерева с корнем в узле А.

Алгоритм вставки с балансировкой.

Каждый узел дерева должен иметь четыре поля: информационное, два указателя на левое и правое поддерево, поле показателя сбалансированности вершины. Процесс добавления вершины:

1. пройти по пути дерева поиска и убедиться, что ключа в дереве нет;

2. включить новую вершину:

3. отступая по пути поиска проверять в каждой вершине показатель сбалансированности, если необходимо, то выполнить балансировку.

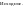
П ример. Вставляем вершину 75. Вершины, входящие в путь поиска:100, 50, 70, 80.

Алгоритм исключение элемента из сбалансированного дерева.

1. Поиск удаляемого элемента

2. Исключение элемента

3. Балансировка.

Если включение одного ключа может привести самое большее к одному повороту (разбалансирована 0 или 1 вершина), то исключение может потребовать балансировки во всех вершинах вдоль пути поиска.

Название поворота	Баланс вершины А	Баланс вершины В	Рисунок
LL	2	1 или 0
RR	-2	-1 или 0
LR	2	-1
RL	-2	1

5.В-деревья. Основные определения и операции.

Иногда требуются деревья больше чем 2 степени, и для них либо не хватает ОП, либо она дорогая. Пусть вершины дерева хранятся в файлах. Для хранения миллиона элементов в двоичном дереве требуется в среднем 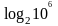обращений. При обращении к одному элементу, находящемуся во внешней памяти, одновременно можно считать и еще некоторое количество элементов. Разобьем множество элементов на подмножество одновременно доступных элементов - страниц. Пусть на каждой странице хранится 100 элементов, тогда количество обращений к дереву из 1000000 элементов вычисляется по формуле 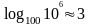. Если хранит корневую вершину в ОП, то снизится до 2.

Для сильноветвящихся деревьев обязательна схема управления их ростом. Предлагаются критерии:

1. каждая страница содержит не более 2n или ключей.

2. каждая страница, кроме корневой содержит не менее n элементов или ключей.

3. каждая страница – это либо лист (нет потомков), либо имеет m+1 потомков, где m-количество ключей на этой странице

4. все страницы – листья, находятся на одном уровне.

Такая структура данных называется В-деревом, величина n – порядком, 4 критерия – свойствами. Т.о. для дерева, состоящего из k элементов порядка n в худшем случае потребуется 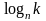обращений к страницам, кроме того коэффициент использования памяти ½ (50%), поскольку страницы заполнены минимум на половину.

С войство бинарного дерева (то что справа – больше, то что слева - меньше) сохраняется.

Поиск в В-дереве.

Е сли спроецировать В-дерево на один уровень, включая потомков между ключами их родительских страниц, то можно заметить, что ключи идут в возрастающем порядке слева на право. Общий вид страниц В-дерева:

k1, k2, …,km – ключи (k1≤k2≤…≤km)

P0,P1,…,Pm – указатели на следующие страницы. Указатель Pi указывает на поддерево ключей больше ki и меньше ki+1 ключа.

Алгоритм.

Пусть задан ключ поиска Х и некоторая страница считана в ОП. Ключ Х ищется соответствующим методом среди ключей k1,k2,…,km. Если ключ найден, то поиск удачен, если поиск не удачен, то возможно три варианта:

1. Х<k1, тогда идем по ссылке Р0

2. X>km, тогда идем по ссылке Рm

3. ki<X<ki+1, тогда идем по ссылке Рi

Если найденный адрес пустой (страницы-потомка не существует), то поиск не удачен. Если указатель не пустой, то в ОП подкачивается следующая страница и процесс повторяется.

Включение элементов в В-дерево.

Требуется вставить новый элемент в В-дерево порядка m. Добавление нового элемента всегда осуществляется в некоторый узел–лист.

Возможны варианты:

1. В вершине-листе есть место для включаемого элемента(добавление заканчивается)

2. Вершина-лист уже содержит 2n ключей. В этом случае новый ключ вставляется в соответствующее место данной вершины. После этого вершина будет иметь 2n+1 ключей, что не допустимо. Поэтому вершину необходимо разделить на 2 вершины, содержащих n ключей каждая, причем в первую вершину войдут k1,…,kn, а во вторую kn+2,…k2n+1. Ключ kn+1 (средний ключ) должен быть включен в вершину-предок данной вершины. Если в вершине-предке было меньше 2n ключей, то процесс заканчивается.

3. Вершина-предок тоже полна, тогда эту вершину также нужно разделить на две. В худшем случае процесс деления распространится на все вершины вплоть до корня, высота дерева увеличится на единицу.

В-дерево растет с низу в верх.

Исключение элемента из В-дерева.

Возможны варианты:

1. Исключаемый элемент находится на листе страницы

2. Элемент не находится на листе, тогда его нужно заменить одним из двух лексикографически смежных элементов. В результате удаление будет все же с листовой страницы.

После удаления элемента нужно проверить не стало ли количество элементов на странице меньше n. Один из вариантов решения – позаимствовать элементы с одной из соседних страниц. Пусть на странице Т удаляется элемент, а со страницы Q заимствуется элемент. В этом случае элементы страницы T и Q, а так же их непосредственный предок, поровну распределяются на обе страницы (средний элемент опять уходит на верх). Этот процесс называется балансировкой страницы. Однако может быть, что на странице Q нечего занимать, т.к. ее размер равен n. В этом случае общее число элементов на странице T и Q равно2n-1. и мы можем слить две строчки в одну, добавив средний элемент из родительской для T и Q страницы. Одна из страниц (Q и T ) уничтожается.

Удаление среднего ключа на родительской странице может вновь привести к тому, что ее размер так же станет меньше n.

В

T

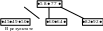худшем случае слияние страниц может распространиться вплоть до корневой вершины. Если корень сократиться до нулевого размера, то он удаляется и высота дерева уменьшается.