Параллельное программирование

1. Параллельная обработка информации в вычислительных системах. Конвейерная обработка. Мультипрограммный режим, формула Литтла. Ярусно-параллельная форма представления программы.

Основные способы организации параллельной обработки информации: есть 3 способа обработки информации:

1.Совмещение во времени различных этапов выполнения различных задач (это мультипрограммный режим)

2.Конвеерная обработка информации

3.Одновременное решение различных задач или различных частей одной задачи.

Первый два способа могут быть реализованы даже в случае однопроцессорных ЭВМ с доменовской архитектурой.

Мультипрограммный режим организуется программными средствами ОС или средствами среды программирования.

Конвейерная обработка – организуется в однопроцессорных ЭВМ на уровне отдельных устройств (внутри микропроцессора организуется конвеер программ: это называется параллелизмом).

Третий способ может быть реализован только в многопроцессорных устройствах.

Мультипрограммный режим, формула Литтла:

Сущность мультипрограммного режима состоит в том, что в системе одновременно обрабатывается несколько задач, между которыми распределяется имеющиеся ресурсы. Наиболее эффективно оно в том случае, если в задаче требуется различные устройства, которые могут функционировать параллельно.

Целью является увеличение производительности в системе.

Число задач одновременно находящихся в системе называется уровнем мультипрограммирования.

λ-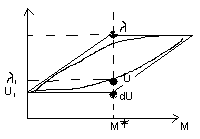 производительность

u- время ответа

М – коэффициент, соответствующий мультипрограммированию

М* - точка насыщения мультипрограммной смеси

С увеличением количества задач производительность системы повышается, а время ответа растет незначительно. Это до тех пор, пока уровень мультипрограммирования не достигнет М*, это значение – количество устройств, которое имеется в системе, используется задачами и могут функционировать параллельно. Значение * - точка нахождения мультипрограммной смеси. Увеличение количества достижения точки насыщения мультипрограммной смеси, очевидно не имеет смысла.

П роизводительность, время ответа и уровень мультипрограммирования связаны между собой формулой Литтла: λ=М/U. Режим мультипрограммной обработки является коэффициент мультипрограммирования. Пусть в системе имеется N устройств, загрузка которых равна p₁…p_n , где p_i=T_i/T. T_i – время в течении которого устройство использовалось (функционировало). T – общее время работы системы. Тогда коэффициент

m= λ/ λ1, где λ – производительность, которая достигнута в системе с мультипрограммированием, λ1 – производительность системы в однопроцессорном режиме. Т.е. коэффициент МП характеризует повышение производительности системы за счет мультипрограммирования.

Конвейерная обработка информации

Предполагает прохождение потока данных через последовательность функциональных блоков, реализующих операции над данными, при этом выполнение операций могут быть совмещено.

Классическим примером задачи является задача сложения векторов. Задачу можно решить организовав конвейер, в котором имеется четыре ci=bi+ai функциональных устройства: 1)для любой пары входных значений элементов векторов осуществляется сравнение порядков

2)Осуществляет выравнивание порядков

3)Сложение мантисс

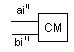
4)Организует нормализацию результатов

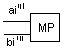
Элемент	СП	ВП	СМ	НР
1	a1b1
2	a2b2	a1b1
3	a3b3	a2b2	a1b1
4	a4b4	a3b3	a2b2	a1b1
….	….	…..	….	….
N	anbn	an-1bn-1	an-2bn-2	an-3bn-3
N+1		anbn	an-1bn-1	an-2bn-2
N+2			anbn	an-1bn-1
N+3				anbn

Без конвейеризации мы вычислили бы задачу по формуле: T1= nΣ(от k до i=1) ti, где к – количество операций, которое вычисляем, t – время, n- количество векторов.

Е2=(n+k-1)*m, где m- длительность самой продолжительной операции.

Виды параллелизма:

1. естественный параллелизм независимых задач(поток не связных между собой задач, решение которых не зависит от решения другой задачи);

2. параллелизм объектов или данных (по одной и той же или почти одной и той же программе должна обрабатываться некоторая совокупность данных, поступающая в систему одновременно, это задачи векторной алгебры)

3. параллелизм независимых ветвей(выделяют отдельные независимые части программы, которые могут выполняться параллельно при наличии нескольких обрабатывающих устройств. критерии, позволяющие выделить независимые ветви:

   • отсутствуют функции связей(входные данные любой ветви не являются выходными данными другой ветви)

   • отсутствуют связи по использованию одних и тех же областей памяти(ветви программы производят запись информации во взаимно не пересекаемые области памяти)

   • независимость по управлению(условие выполнение ветви не зависит от результатов или признаков, полученных при выполнении другой ветви)

   • программная независимость – ветви должны выполняться по разным блокам программы).

это наиболее явная форма программного параллелизма м.б. представлена в виде ярусно –параллельной формы.

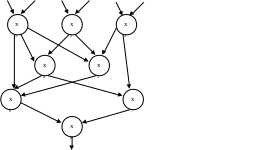
ярус 1

ярус 2

ярус 3

ярус 4

вершины графа x₁…х₈ ветви программы

Каждый ярус обрабатывается независимыми ветвями, отвечающими ранее выделенным критериям. Независимые ветви могут выполняться одновременно. Дуги обозначают входные и выходные данные и промежуточные результаты, связывающие между собой различные ярусы.