2.1.2. Несколько независимых переменных

В тех случаях, когда аппроксимируемая переменная у зависит от нескольких независимых переменных у = f(х₁, х₂,…, х_n) используется следующие специальные функции MS Excel:

ЛИНЕЙН и ТЕНДЕНЦИЯ для аппроксимации линейных функций вида:

 у = а₀ + а₁х₁ + а₂х₂ + … + а_nx_n.

ЛГРФПРИБЛ и РОСТ для аппроксимации показательных функций вида:

Функции ЛИНЕЙН и ЛГРФПРИБЛ имеют одинаковые параметры.

Функции ТЕНДЕНЦИЯ и РОСТ позволяют находить точки, лежащие на аппроксимирующих кривых. Обе функции имеют одинаковые параметры.

Пример. Менеджерами магазина в течение недели собирались данные о прибыли от продажи товаров в зависимости от числа посетителей магазина и числа покупок. В результате была получена таблица данных. Требуется построить таблицу, отражающую динамику прибыли в зависимости от числа посетителей (от 100 до 130) и числа покупок (от 15 до 25) с шагом ∆ = 5. 

x1	x2	Прибыль %
120	20	32,5
100	25	28,3
130	20	33,7
100	15	33,1
110	23	30,5
105	26	39,1
112	16	38,4

 Требуется построить эмпирическую таблицу, отражающую динамику прибыли в зависимости от числа посетителей (от 100 до 130) и числа покупок (от 15 до 25) с шагом 5.

Решение:

Организуем данные на листе Excel, оставив пустой диапазон для у. (рис. 5).

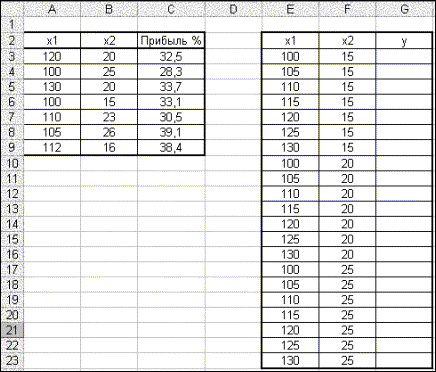
 Рис. 5. Исходные данные на листе Excel

 Выделим диапазон G3:G23 для у, вызовем функцию ТЕНДЕНЦИЯ и укажем для нее параметры (рис. 6): 

 Рис. 6. Функция тенденция 

Нажмем сочетание клавиш CTRL+SHIFT+ENTER и получим результат в столбце у (рис. 7):

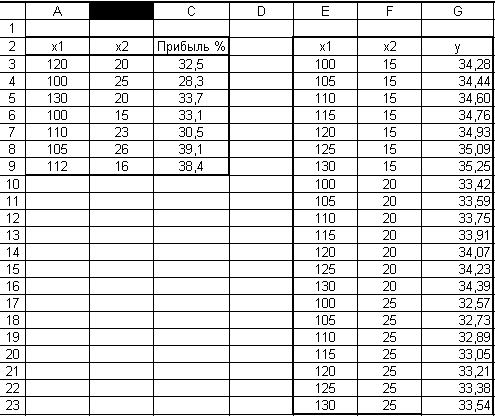
 Рис. 7. Итоговое значение

 Задание 2

Решить задачу, рассмотренную в примере с новыми исходными данными: число посетителей выбрать произвольно в пределах от 50 до 200, а число покупок от 1 до 30.

 

2.2. Модели линейной оптимизации в ms excel

2.2.1. Решение задач линейного программирования в ms excel

Очень часто математическая постановка экономических задач, связанных с управлением, может быть сформулирована в общем виде следующим образом.

Пусть имеет некоторая целевая функция z, которая зависит от параметров , удовлетворяющих некоторым ограничениям α.

z = z(x,α).

Требуется найти такие значения параметров или функций, которые обращают величину z в максимум или минимум. Такие задачи – отыскание значений параметров, обеспечивающих экстремум функции при наличии ограничений, наложенных на аргументы, – носят общее название задач математического программирования и решаются ме­тодами теории исследования операций.

Среди задач математического программирования самы­ми простыми являются задачи линейного программирова­ния (ЗЛП).

Основная задача линейного программирования (ОЗЛП) заключается в нахождении неотрицательных значений переменных, удовлетворяющих условиям – равенствам и обращающие в максимум линейную функцию этих переменных. Допустимое решение, максимизирующее целевую функцию называется оптимальным решением (оптимальным планом).

Инструментом для решений задач оптимизации в MS Ехсеl служит надстройка Поиск решения. Процедура поиска решения позволяет найти оптимальное значение фор­мулы, содержащейся в ячейке, которая называется целевой. Эта процедура работает с группой ячеек, прямо или косвенно связанных с формулой в целевой ячейке. Чтобы получить по формуле, содержащейся в целевой ячейке, заданный результат, процедура изменяет значения во влияющих ячейках.

Если данная надстройка установлена, то Поиск решения запускается из меню Сервис. Если такого пункта нет, следует выполнить команду Сервис → Надстройки... и выставить флажок против надстройки Поиск решения.

Решения задачи оптимизации состоит из нескольких этапов.

А. Создание модели задачи оптимизации.

В. Поиск решения задачи оптимизации.

С. Анализ найденного решения задачи оптимизации.

Пример

Предприятие выпускает два вида железобетонных изделий: лестничные марши и балконные плиты. Для производства одного лестничного марша требуется 3,5 куб.м. бетона и 1 упаковку арматуры, а для производства плиты 1 куб.м. бетона и 2 упаковку арматуры. На каждую единицу продукции приходится 1 человеко-день трудозатрат. Прибыль от продажи одного лестничного марша составляет 200 руб., а одной плиты – 100 руб. На предприятии работает 150 человек, причем известно, что в день предприятие получает не более 240 упаковок арматуры и производит не более 350 куб.м. бетона. Требуется составить производственный план, чтобы прибыль была максимальной

Решение

1.  На листе рабочей книги EXCEL заполните таблицу параметров задачи.

2.  Составьте модель задачи и заполните ячейки для значений переменных (первоначально ячейки х1 и х2 заполняются числовыми значениями, например, значением 10), целевой функции (ячейка содержит формулу) и ограничений (ячейки содержат формулы) (рис. 8).

 

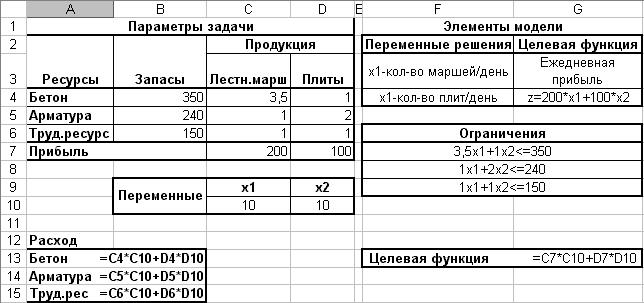
Рис. 8. Параметры задачи 

3.  Выполните команду Сервис →Поиск решения и установите необходимые значения в полях диалогового окна Поиск решения, добавляя ограничения в окне Добавление ограничений (рис. 9).

 

 

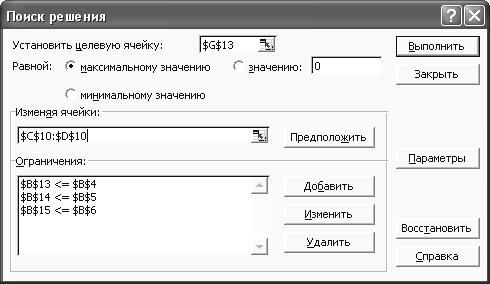
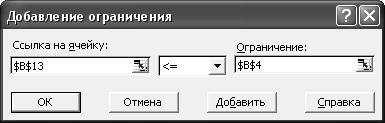
 Рис. 9. Окно Поиск решения.

 4.  Нажмите на кнопку Выполнить. На экране появится окно Результаты поиска решения (рис. 10). 

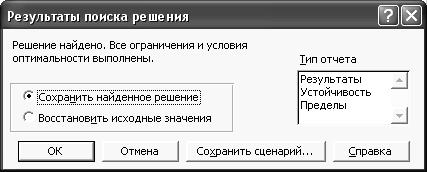
 Рис. 10. Результаты поиска решений

 В случае ошибок в формулах, ограничениях или неверных параметрах модели в данном окне могут появиться следующие сообщения: «Значения целевой ячейки не сходятся», «Поиск не может найти решения» или «Условия линейной модели не выполняются». При этом переключатель следует установить в положение Восстановить исходные значения, проверить данные на листе и процедуру поиска повторить снова.

5.  В результате в ячейках с переменными задачи появятся значения соответствующие оптимальному плану (80 лестничных маршей и 70 плит в день), а в ячейке для целевой функции – значение прибыли (23000 руб.), соответствующее данному плану (рис. 11).

 

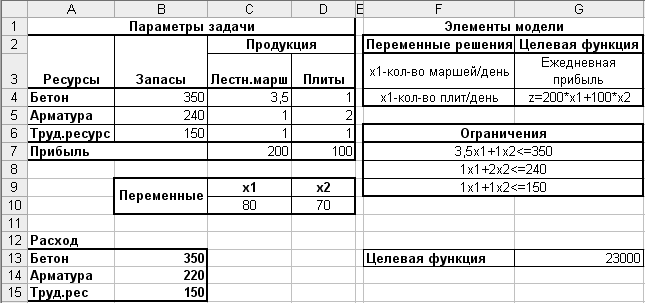
 Рис. 11. Параметры задачи

 6.  В случае если полученное решение является удовлетворительным, можно сохранить оптимальный план и ознакомиться с результатами поиска, которые выводятся на отдельный лист (рис. 12).

 

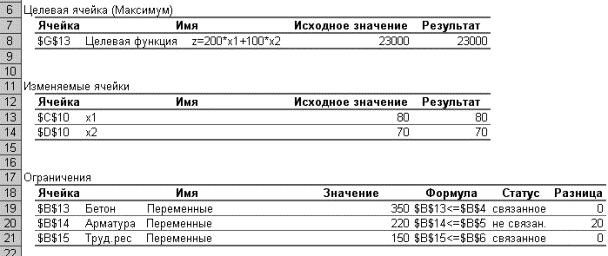
Рис. 12. Результаты поиска