Деление

Пусть отношение R определено на множестве атрибутов А, а отношение S – на множестве атрибутов В, причем В А (т.е. В является подмножеством А). Пусть С=А-В, т.е. С является множеством атрибутов отношения R, которые не являются атрибутами отношения S.

Деление R÷S – результатом является набор кортежей отношения R (определено на множестве атрибутов А), определенных на множестве атрибутов С (С=А-В), которые соответствуют комбинации всех кортежей отношения S (определено на множестве атрибутов В).

Этот оператор можно сформулировать и на основе других основных операторов:

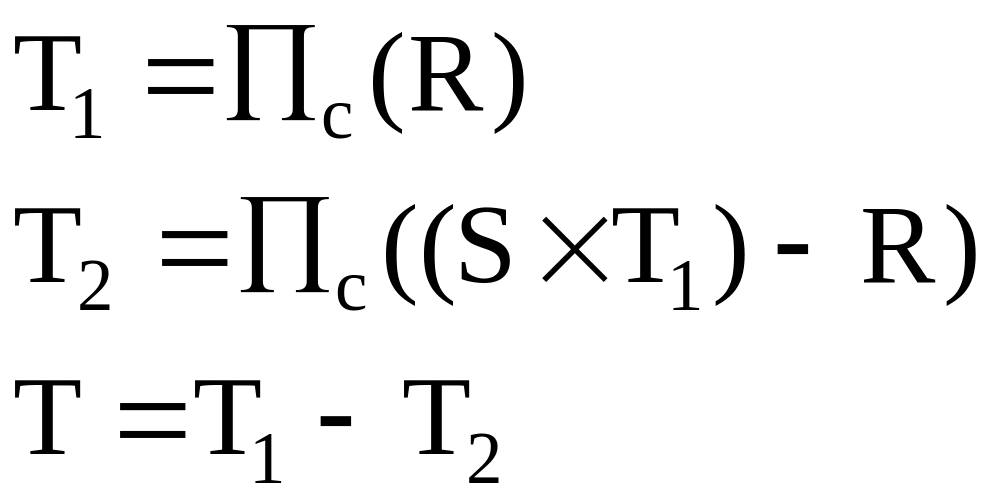
Пример.

Отношение R

Номер группы	Количество студентов	ФИО куратора	Код предмета	Название предмета
ТМ-31	20	Иванов	01	Математика
ТМ-32	22	Петров	01	Математика
ТИ-31	13	Сидоров	01	Математика
ТМ-31	20	Иванов	02	Физика
ТМ-32	22	Петров	02	Физика

Отношение S

Номер группы	Количество студентов	ФИО куратора
ТМ-31	20	Иванов
ТМ-32	22	Петров
ТИ-31	13	Сидоров

T1: Select’Код предмета’, ’Название предмета’ from R

Код предмета	Название предмета
01	Математика
02	Физика

T21: Select * from T1, S

Код предмета	Название предмета	Номер группы	Количество студентов	ФИО куратора
01	Математика	ТМ-31	20	Иванов
01	Математика	ТМ-32	22	Петров
01	Математика	ТИ-31	13	Сидоров
02	Физика	ТМ-31	20	Иванов
02	Физика	ТМ-32	22	Петров
02	Физика	ТИ-31	13	Сидоров

T22: (Select * from T21) exept (Select * from R)

Код предмета	Название предмета	Номер группы	Количество студентов	ФИО куратора
02	Физика	ТИ-31	13	Сидоров

T2: Select ’Код предмета’, ’Название предмета’ from T22

Код предмета	Название предмета
02	Физика

Р=T₁-T₂

Код предмета	Название предмета
01	Математика

Рис. 2.45. Пример операции деления.

Реляционное исчисление

В выражениях реляционной алгебры всегда явно задается некий порядок, а также подразумевается некая стратегия оценки запроса. В реляционном исчислении не существует никакого описания оценки запроса, поскольку в запросе реляционного исчисления указывается, что следует извлечь, а не как.

Реляционное исчисление никак не связано с дифференциальным и интегральным исчислениями в математике, а его название произошло от части символьной логики, которая называется исчислением предикатов.

В контексте баз данных оно существует в двух формах:

1. В форме предложенного Коддом реляционного исчисления

кортежей.

2. В форме предложенного Лакруа и Пиро реляционного исчисления

доменов.

Предикат в логике первого порядка (или теории исчисления предикатов) – истинностная функция с параметрами.

Суждение – выражение, которое принимает функция после подстановки значений вместо параметров. Может быть истинным или ложным.

Например, предложения "Иванов является студентом данного института" и "Стипендия Иванова выше, чем у Петрова" являются суждениями, поскольку можно определить их истинность или ложность. В первом случае функция "является студентом данного института" имеет один аргумент ("Иванов"), а во втором случае функция "стипендия выше" имеет, два аргумента ("Иванов" и "Петров").

Если предикат содержит переменную, то у этой переменной должна быть соответствующая область определения.

При подстановке вместо переменной х одних значений из ее области определения суждение может оказаться истинным, а при подстановке других – ложным.

Если областью определения являются все люди, и мы подставим вместо переменной х значение "Иванов", то суждение "Иванов является студентом данного института" будет истинным. Если же вместо переменной х подставить имя другого человека, который не является студентом данного института, то суждение будет ложным.

Если Р – предикат, то множество всех значений переменной х, при которых суждение Р становится истинным, можно символически записать следующим образом:

Предикаты могут соединяться с помощью логических операторов: (AND), (ОR) и ¯ (NOT) с образованием составных предикатов.