11. Вычисление объема тела.

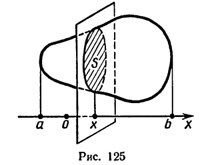
Пусть задано тело объемом V, причем имеется такая прямая (рис. 1), что, какую бы плоскость, перпендикулярную этой прямой, мы ни взяли, нам известна площадь S сечения тела этой плоскостью. Но плоскость, перпендикулярная оси Ох, пересекает ее в некоторой точке х. Следовательно, каждому числу х (из отрезка [а; b] см. рис. 1) поставлено в соответствие единственное число S (х) — площадь сечения тела этой плоскостью. Тем самым на отрезке [а; b] задана функция S (х). Если функция S непрерывна на отрезке [а; b] то справедлива формула Полное доказательство этой формулы дается в курсах математического анализа, а здесь остановимся на наглядных соображениях, приводящих к ней. Разобьем отрезок [а; b] на n отрезков равной длины точками x₀ = a <x₁ <x₂ <... <x_n-1 <b=х_n, и пусть

Через каждую точку х_k проведем плоскость, перпендикулярную оси Ох. Эти плоскости разрезают заданное тело на слои (рис. 2, а, б). Объем слоя, заключенного между плоскостями α_k-1 и α_k, при достаточно больших n приближенно равен площади S(x_k-1) сечения, умноженной на «толщину слоя» Δx, и поэтому Точность этого приближенного равенства тем выше, чем тоньше слои, на которые разрезано тело, т. е. чем больше n. Поэтому V_n →V при n → ∞. По определению интеграла при n → ∞.

12Двойной интеграл в прямоугольных координатах.

 Двойным интегралом от функции f (x, y) по области D называется предел, к которому стремится n-я интегральная сумма при стремлении к нулю наибольшего диаметра частичных областей:

.

При f (x, y) > 0, (поверхность Z = f (x, y) целиком лежит в верхней полуплоскости) двойной интеграл равен объему цилиндрического тела ограниченного областью D и поверхностью Z = f (x, y).

Если функция f (x, y) непрерывна в области D, ограниченной замкнутой линией, то ее n-я интегральная сумма стремится к пределу при стремлении к нулю наибольшего диаметра частичных областей. Этот предел, т.е. двойной интеграл  , существует и не зависит от способа разбиения области D на частичные области и от выбора в них точек M_k.

Основные свойства двойных интегралов

1. Двойной интеграл от суммы конечного числа функций равен сумме двойных интегралов от слагаемых функций:

 (90)

2. Постоянный множитель подынтегральной функции можно вынести за символ двойного интеграла:

 (91)

3. Если область интегрирования разбита на две части D₁ и D₂, то

. (92)

4. Если во всех точках области D функции f (x, y) и   удовлетворяют условию  , то

. (93)

Знак неравенства может перейти в знак равенства только при совпадении функций.

С л е д с т в и е. Если подынтегральная функция в области интегрирования не меняет знака, то двойной интеграл есть число того же знака, что и функция.

5. Если функция f (x, y) во всех точках области интегрирования удовлетворяет неравенствам

,

то

,

где S – площадь области D.

6. Двойной интеграл равен произведению значения подынтегральной функции в некоторой точке области интегрирования на площадь области интегрирования, т.е.

.

Значение   из (95) называется средним значением функции f (x, y) в области D, а равенство (95) является, по существу, обобщением теоремы о среднем для определенного интеграла на двойной интеграл.