20. Методика изучения взаимного расположения прямых в пространстве. Скрещивающиеся прямые.

Возможны 3 случая взаимного расположения прямых в пространстве:

1. Прямые пересекаются(имеют 1 общую точку);

2. Прямые параллельны(лежат в одной плоскости и не пересекаются);

3. Прямые скрещиваются(не сущ. Плоскости в которой они обе лежат).

Определение: 2 прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Пишут .

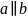Можно поставить в хорошем классе проблемный вопрос: могут ли 2 прямые в пространстве располагаться так, что через них нельзя провести плоскость? Показ. В окруж. Действительности, на моделях, что они не могут иметь общих точек, ввести термин «скрещивающиеся прямые», показать обозначение.

Определение: две прямые называются скрещивающимися, если не существует плоскости, в которой они обе лежат.

Следует особое внимание уделить признаку, который лежит в основе их построения: если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.

Перед формулировкой признака проиллюстрировать скрещивающиеся прямые используя каркасные модели многогранников и подметить следующие особенности: одна из прямых пересекает плоскость в которой лежит другая прямая, в точке, не принадлежащей ей. Выполняется рисунок, дается формулировка и выполняется доказательство.

Доказ. Следует рассказать учителю, а затем пусть учащиеся повторят его. При док-ве заострить внимание уч-ся на вопрос: что значит, 2 прямые не являются скрещивающимися??(пересекаются или параллельны). В задачах на закрепление должны быть рассмотрены все возмож. Скрещ. прямые, которым принадлежат ребра многогранников.

22. Методика изучения перпендикулярности прямых в пространстве.

Перпендик-ть прямых в пространстве в уч. ШЛ. логично вводится в главе «Паралл-ть прямых и плоскостей» в § Угол между прямыми. Автор отмечает, что углом между двумя пересекающимися и скрещивающимися прямыми явл. наим. угол среди 4-х образованных. Угол между прямыми удовлетворяет условию 0˚<α≤90˚. Если прямые образуют 4 равных угла, то угол между этими прямыми равен 90˚. Затем дает определение взаимно перпендик-ых прямых(перпендик-ых).Это определние уч-ся могут сформулировать сами.Опр: Две прямые наз. вз. перпендик-ми(перпендикул-ми), если угол между ними равен 90˚. И далее в учебнике идет: Если прямая а перпендикулярна прямой b, то пишут а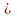 b и читают: «Прямая а перпендикулярна прямой b». Важно отметить, что из опр. следует, что перпенд-ые прямые могут пересекаться, а могут быть скрещивающимися

21. Методика изучения параллельности

Наиболее сложный признак параллельности плоскостей. Он осуществляется методом от противного. При этом в пособии рисунков нет, учитель должен сам предоставить рисунки. При объяснении следует ссылаться на изученный материал параллельности прямых, параллельности прямой и плоскости.

Определение. Две плоскости называются параллельными, если они не пересекаются.

Представление о параллельных плоскостях дают, например, пол и потолок комнаты, поверхность пола и стоящего на нем стола, противоположные стенки шкафов и др.

Теорема (признак параллельности плоскостей).Если, две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Доказательство.

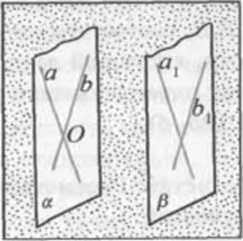
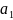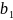Пусть даны две плоскости ɑ и ß. В плоскости лежат ɑ пересекающиеся в точке О прямые a и b плоскости ß — прямые и такие, что а II и b || Заметим, что каждая из прямых а и b параллельна плоскости ß (а II ß, b || ß).

Предположим, что плоскости ɑ и ß не параллельны. Пусть они пересекаются по прямой с. Тогда плоскость ɑ проходит через прямую а, параллельную плоскости ß, и пересекает плоскость ß по прямой с, следовательно, прямая а параллельна прямой с. Аналогично плоскость ɑ проходит через прямую b, параллельную плоскости ß, и пересекает ее по прямей с, значит, прямая b параллельна прямой с.

Таким образом, исходя из предположения, получили, что через точку О проходят две прямые а и b, параллельные прямой с. Но это противоречит теореме о том, что через точку О проходит единственная прямая, параллельная прямой с. Следовательно, наше предположение неверно и плоскости ɑ и ß параллельны.