3.4. Методика изучения длины и градусной меры в школьном курсе математики.

Мотивация: 1) умеем сравнивать числа, а отрезки? 2) ученики умеют из нач шк измерять длины отрезков линейкой, и выражать её разл ед измерения, напр: 1м=10дм=100см =

= 1000мм, повторив матер в 5-ом классе учитель вводит понятие ед отрезка как отрезка, длина кот прин за единицу измерения. Ученики должны понимать, что измерить длину отрезка – это зн найти сколько ед отрезков содерж в данном отрезке. На интуитивно-нагл уровне установить свойства длины: - если отрезки равны, то равны их длины, - если точка разбивает отрезок на две части, то длина его равна сумме длин его частей.

Главный вывод: отрезки можно сравнивать с пом наложения или с пом измер их длин.

Новым в 7-ом классе явл введение опр длины отрезка: Длина отрезка – геом величина, кот показывает сколько раз его ед измерения и её части укладываются в измеряемом отрезке. Вывод: при выбранной ед измерения длину отрезка можно выразить некот полож числами.

В проц беседы с уч-ся фактически формул все аксиомы, кот наз св-ми длины отрезков:

1. Каждый отрезок имеет длину больше 0. (при выбранной ед измер)

2. Для любого полож числа сущ отр, длина кот выр-ся этим числом (при выбр ед изм)

3. Равные отрезки имеют равные длины.

4. Отрезки, имеющие равные длины равны.

5. Длина отрезка равна сумме длин отрезков, на кот он делится любой точкой.

С понятием окру ч-ся знакомы с нач школы, в 6-ом кл ставится зад найти длину окр С. Для этого с уч-ся нужно провести практическую работу, авторы предлагают опоясать оо колеса полоской бумаги и сравнить длину полоски с диаметром колеса, но это нереально. В результате практической работы получается вывод: отношение c/d явл одним и тем же числом для любой окружности, обозн Пи=3,14, записывается формула С=Пи*d, C=2*Пи*R – эти формулы надо взять в рамочки и работать по их закреплению. Формула S=2*Пи*R² дается в учебнике в готовом виде, система упражнений для закрепления формулы в учебнике есть.

В 9-ом классе опр длины окружности вводится след образом: за длину окр-сти приним число к которому стремятся периметры вписанных в окружность правильных многоуг, при неогранич увелич числа их сторон.

В учебнике в виде Т док-ся факт, что c/d=const, при этом периметр выражается через стороны, а стороны через радиус описанных окружностей.

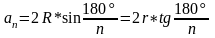
Градусная мера изучается в 5 кл по учебнику латотина чеботаревского в первой части в теме : «окружность, круг, угол». Вначале изучения данной темы хорошо было бы провести с учениками беседу по теме «градус». В данной теме изучается: как измеряется угол транспортиром, что такое транспортир, градусная мера 1/180 развернутого угла, градус обозначается кружочком, описывается поэтапно как измерить угол, величина угла в градусах называется градусной мерой угла, как с помощью транспортира можно построить угол заданной меры.

13. Методика изучения площадей планиметрических фигур.

В 5-ом классе мы мотив необход изуч площадей след образом: умеем сравнивать отрезки, углы, как сравн прямоуг (налож, подсч сколько ед квадр будет). Затем предл 2-3 рис прямоуг, разбитых на ед квадр, предл подсчитать площадь, затем обобщить, записать формулу S=a*b и добиться усвоения формулировки (S_{прямоуг}=произведению его измерений). Как частный случай выводится формула S=a². Повторить ед. измер, перевод одних в др.

В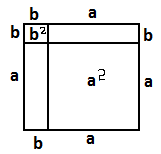 8-ом кл вводится понятие S. Это полезно сделать вместе с уч-ся, исп метод аналогии с длиной отрезка. Опять учителю приходится возвр к изуч S прямоуг, это связано с тем, что учитель должен мотив изуч мат тем, что ф-ла S прямоуг, была раньше получена для S прямоуг, длины сторон кот явл нат числами. Встает вопрос: будет ли формула верна, если это не так (длины сторон выражаются числами, несоизмеримыми с ед измер). В связи с этим авторы предл рассм. произв. прямоуг.

Прямоуг достр до квадрата со стор a+b и выражается S квадрата:

(a+b)²=a²+b²+2S. a²+2ab+b² - a² – b² = 2S. S=2ab.

Вывод формул для измер Sпараллелограмма, треуг, трап, не вызывает затруднения, поэтому при умелом руководстве учителя этот материал

может изучаться сам-но: S паралл-ма нах-ся с пом построения прямоуг, S треуг достраиванием до парал-ма, Sтрап как сумма S треуг.

При изучении S круга учитель должен мотивировать необх нового df S тем, что мы не можем использовать идею заполнения круга конечным числом квадратов. Ф-ла S круга давалась в готовом виде в 6-ом классе. В 9-ом кл вводится след df: За S круга принимается число к кот стремятся площади вписанных в окружность, ограничивающую этот круг правильных n-угольных фигур при неогр увелич числа их сторон. Док-во проводится с пом уч-ся, т.к. опирается на знания ф-л S многоуг.