19/Основные методы решения функциональных уравнений (метод Коши, функциональные замены).

Функциональное уравнение — это уравнение, в котором неизвестными являются функции (одна или несколько). f(-x)=f(x)- простейшее.

Решить функциональное уравнение — значит, найти неизвестную функцию, при подстановке которой в исходное функциональное уравнение оно обращается в тождество (если неизвестных функций несколько, то необходимо найти их все).

F(x) наз решением ФУ, если она удовлетворяет ему при всех значениях аргумента в области ее определения.

Многие ФУ содержат несколько переменных. Все эти переменные, если на них не наложены какие-то ограничения, являются независимыми.

Всегда четко должно быть оговорено, на каком множестве функциональное уравнение задается, т.е. какова область определения каждой неизвестной функции. Общее решение функционального уравнения может зависеть от этого множества.

Кроме области определения функций, важно знать, в каком классе функций ищется решение. Количество и поведение решений очень строго зависит от этого класса.

В школьном курсе не рассм уравнения, не сводящихся к дифференциальным или интегральным, известно очень мало общих методов решения. 

Основные типы:

1. f(x+y)=f(x)*f(y) – удовл. показательные функции.

2. f(xy)=f(x)+f(y) - удовл. логарифмические функции.

3. Уравнение Коши: f(x+y)=f(x)+f(y)

4. f(x+y)+f(x-y)=2 (f(x)+f(y)) – квадратные функции.

5. ур’е Лобачевского f(x+y)*f(x-y)=2 f(x)

Основные методы:

1. метод Коши,

2функциональные замены(подстановки): Заменяя некоторые переменные ФУ либо конкретными значениями, либо какими-либо другими выражениями пытаемся либо упростить это уравнение, либо привести его к такому виду, что что позволяет найти f(x).

7. Целые числа

1. Делимость целых чисел. Свойства делимости. Теорема о делении с остатком

Определение. Пусть a,b— целые числа. Говорят, что число a делится на b, если a можно представить в виде a=nb, где n— целое число.

Иначе: b— делитель.

Обозначение:.

Свойства делимости

Пусть a,b,c,d— целые числа, число p— простое.

1. Если в равенстве a+b=c два числа делятся на d, то и третье число делится на d.

2. Если:. , то:. .

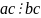3. Если :. и , то :. .

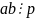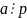4. Если : , то либо : , либо : .

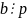Теорема. Всякое целое a представляется единственным способом с помощью целого равенством вида , где q,r— целые, . Число q называется частным, r — остатком от деления a на b.

2. Сравнения и их свойства

Определение. Пусть a и b— целые числа, m— натуральное число. Говорят, что a сравнимо с b по модулю, m если при делении на m они дают одинаковые остатки.

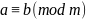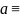Обозначение: или _mb.

Теорема. a сравнимо с b по модулю m тогда и только тогда, когда :. .

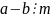Свойства сравнений

1) 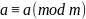(рефлексивность).

2) (симметричность).

3) (транзитивность).

4)

Китайская теорема об остатках/рамка:

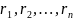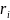Если числа попарно взаимно просты, то для любых остатков таких, что при всех i=1,2,…n, найдётся число , которое при делении на даёт остаток при всех i=1,2,…n.