22 Вопрос

Теорема Чевы.

Пусть на сторонах треугольника ABC выбраны точки A₁ϵBC, B₁ϵ AC, C₁ ϵAB. Отрезки AA₁, BB₁, CC₁ пересекаются в одной точке тогда и только тогда, когда выполняется равенство:

= 1

Доказательство

Необходимость. Пусть отрезки AA₁, BB₁, CC₁ пересекаются в одной точке O. Проведем через вершину B треугольника прямую a║AC Пусть прямые AA₁ и BB₁ пересекают прямую a в точках M и N соответственно. Тогда из подобия треугольников AA₁C и MA₁B₁ по двум углам (< A₁CA = < A₁BM как накрест лежащие и < BA₁M = < AA₁C как вертикальные) имеем:

.

Аналогично из подобия треугольников AC₁C и BC₁N по двум углам ( < C₁CA = < C₁NB и < C₁AC = < C₁BN – как пары накрест лежащих):

.

Наконец, из подобия треугольников OAC и OMN по двум углам ( < OCA =< ONB и <OAC = < OMN) получаем =

Перемножив соответственно правые и левые части выписанных равенств, получим необходимое равенство.

Достаточность. Пусть выполнено равенство. Покажем, что отрезки AA₁, BB₁, CC₁ проходят через одну точку.

Пусть O – точка пересечения отрезков AA₁ и CC₁ а C' – точка пересечения отрезка AB с лучом CO. Тогда из только что доказанного следует, что

= 1

Теорема Менелая. Пусть дан треугольник ABC и точки C₁, B₁, A₁ на, соответственно, прямых AB, AC и BC. Точки C₁, B₁, A₁ лежат на одной прямой тогда и только тогда, когда выполняется равенство

= 1

17.Числовые последовательности.

df. Конечной числовой последовательностью яв-ся любой конечн.набор действит-х чисел, каждое из кот-х имеет свой номер, т.е. N-ое число, поставленное в соответствии данному действ-ому .

Если таких номеров конечное число, то последовательность конечна.

df.Если же любому N-ому числу поставлено в соотв-ии некоторое действит. число(единствен.), то послед-ть явл. бесконечной.

Свойства послед-тей:

(*) Посл-ть наз. ограничен.сверху , если сущ-ет такое число А,что для любого номера n верно неравенство ,т.е. любой член послед-ти не превосходит некот-го числа.(Пр. посл-ть ,т.к . )

Числовая послед-ть ограничена снизу, если сущ-т такое число В, что для дюбого номера n выпол-ся нер-во (Пр. посл-ть ,т.к. люб.член )

Числ.послед-ть наз.ограниченной,если она огранич. и сверху,и снизу.

Арифметическая прогрессия.

df Числ.посл-ть наз. арифметической прогрессией, если люб.её член, начиная со второго,равен предыдущему,сложенному с одним и тем же числом .

Формула n-го члена ариф.прог.:

Свойство членов ариф.прог.: кажд.член ариф.прог.,начиная со 2-го=среднему арифметич.2-х соседних с ним ( )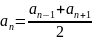

Формула суммы первых членов ариф.прог.:

Геометрическая прогрессия.

dfГеометр.прогр.-это числовая пос-ть, каждый член, начиная со второго, равен предыдущему, умноженному на одно и тоже число q,называемое знаменателем геом. Прогр.,причём q≠0,│ q│≠1.

,где q≠0,│ q│≠1.

Формула n-го члена геомет.прог.:

Свойство геом. Прогрессии: кажд.член геомет.прогрессии,начиная со 2-го ,есть среднее геометрич-ое 2-х соседних с ним: .

Бесконечно убывающая геом.прогрессия- это бескон.геометр.прогрессия, знаменатель кот│ q│<1.

Сумма всех членов бесконечн.прогрессии есть конечн.число определяемое формулой:

Рекуррентная последов-ть.

Для линейных рекуррентных последовательностей существует формула, выражающая общий член последовательности через корни её характеристического многочлена

Для чисел Фибоначчи такой формулой является формула Бине.