6. Задачи с цифрами, арифметические (числовые) ребусы

Числовые ребусы

Другое название - математические ребусы. К такому виду задач относятся математические выражения (обычно простое равенство), в котором все или часть цифр заменены на некоторые значки (буквы, звездочки и т.д.). Требуется вместо каждого значка подставить нужную цифру, чтобы выражение было верным.

Есть несколько общих правил: если в математическом ребусе используются несколько букв, и найдено соответствие между какой-то буквой и цифрой, то другие буквы эту же цифру обозначать не могут; ноль не может быть крайней левой цифрой в числе.

ПРИМЕР

Прежде чем приступить к разгадыванию сложных задач, потренируйтесь на простом примере: ВАГОН+ВАГОН=СОСТАВ. Запишите его в столбик, так будет удобнее решать. Вы имеете два неизвестных пятизначных числа, сумма которых шестизначное число, значит В+В больше 10-ти и С равно 1. Замените символы С на 1.

Сумма А+А – однозначное или двухзначное число с единицей на конце, это возможно в том случае, если сумма Г+Г больше 10 и А равно либо 0, либо 5. Попробуйте предположить, что А равно 0, тогда О равно 5-ти, что не удовлетворяет условиям задачи, т.к. в этом случае В+В=2В не может равняться 15-ти. Следовательно, А=5. Замените все символы А на 5.

Сумма О+О=2О – четное число, может быть равна 5 или 15 лишь в том случае, если сумма Н+Н – двухзначное число, т.е. Н больше 6-ти. Если О+О=5, то О=2. Это решение неверно, т.к. В+В=2В+1, т.е. О должно быть число нечетное. Значит, О равно 7-ми. Замените все О на 7.

Легко заметить, что В равно 8-ми, тогда Н=9. Замените все буквы на найденные числовые значения.

Замените в примере оставшиеся буквы на числа: Г=6 и Т=3. Вы получили верное равенство: 85679+85679=171358. Ребус отгадан.

Некоторые математические ребусы могут иметь несколько решений. Например, для АВС+СВА=ZZZ, А может принимать значения 1; 2; 3. Соответственно, В равно 2; 3; 4, и Z равно 4; 6; 8.

8. Простые числа(определение, формула простого числа, решето Эратосфена). Натуральное число р>1 называется простым, если оно имеет только два делителя: 1 и р.

Критерий простого числа: Натуральное число а является простым тогда и только тогда, когда оно не делится ни на одно простое число р вплоть до простого числа р с индексом n, такого что .

Доказательство.

Необходимость. Если число а простое, то оно не делится ни на одно простое число отличное от числа а и ни на одно простое число вплоть до р, такого, что .

Достаточность. Пусть число а не делится ни на одно простое число вплоть до простого числа р, такого что . Преположим, что число а –составное, т.е. пусть ( . Сред этих чисел и есть хотябы одно число, которое меньше, чем р. Потому что если бы оно было больше чем р, то число было бы больше или равно , а это противоречит условию. Всякое натуральное число имеет по крайней мере хотя бы один простой делитель, а это означает, что , . C другой стороны мы имеем 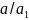и . Число . 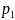Получилось, , - простое число, а это противоречит условию критерия.

Решето Эратосфена – простой старинный алгоритм нахождения всех простых чисел до некоторого целого числа n. Он был создан древнегреческим математиком Эратосфеном. Запишем натуральные числа начиная от 2 до 20 в ряд: 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20. Первое число в списке 2 – простое. Пойдём по ряду чисел, вычёркивая все числа кратные 2. Следующее не вычеркнутое число 3 – простое. Пойдём по ряду чисел, вычёркивая все числа кратные 3 и т.д. Необходимо провести вычёркивания кратных чисел для всех простых чисел р. В результате все составные числа будет вычеркнуты, а невычеркнутыми останутся все простые числа.