
- •Методика решения задач на построение на плоскости.
- •Задачи и содержание школьного курса стереометрии.
- •1. Формирование пространственных представлений.
- •2. Развитие логического мышления у уч-ся:
- •3. Дальнейшее ознакомление с прикладным аппаратом и приложением классической о современной геометрии.
- •Особенности рассмотрения правил изображения фигур в пространстве.
- •Методика введения аксиом стереометрии.
- •Методика доказательства первых теорем курса стереометрии.
- •Докажем, что такая плоскость существует.
- •Докажем единственность этой плоскости.
- •Докажем существование плоскости.
- •Докажем, что такая плоскость единственная.
- •Методические особенности обучения школьников решению задач на построение сечения многогранников.
- •Методика изучения взаимного расположения прямых в пространстве. Скрещивающиеся прямые.
- •Методика изучения параллельности прямых в пространстве.
- •Методика изучения параллельности прямой и плоскости.
- •2. Существование;
- •3. Единственность;
- •Методика изучения перпендикулярности прямых в пространстве
- •Методика изучения перпендикулярности прямой и плоскости.
- •Методика изучения перпендикулярности плоскостей.
- •Методика обучения учащихся нахождению углов между прямыми, прямой и плоскостью, двумя плоскостями.
- •Методика обучения учащихся нахождения расстояния между прямыми, прямой и плоскостью, двумя плоскостями.
- •Особенности изучения многогранников в 5-10 классах.
- •Содержание и цели изучения темы «Многогранники» в 11 классе.
- •Различные подходы к введению понятия «Многогранник» в различных учебных пособиях.
- •Методологические линии изучения многогранников и их характеристики.
- •Методика изучения понятия «призма», элементов и свойств призмы.
- •Методика изучения правильных многогранников.
Методика изучения перпендикулярности прямых в пространстве
Перпендик-ть
прямых в пространстве в уч. ШЛ. логично
вводится в главе «Паралл-ть прямых и
плоскостей» в § Угол между прямыми.
Автор отмечает, что углом между двумя
пересекающимися и скрещивающимися
прямыми явл. наим. угол среди 4-х
образованных. Угол между прямыми
удовлетворяет условию 0˚<α≤90˚. Если
прямые образуют 4 равных угла, то угол
между этими прямыми равен 90˚. Затем дает
определение взаимно перпендик-ых
прямых(перпендик-ых).Это определние
уч-ся могут сформулировать сами.Опр:
Две прямые наз. вз. перпендик-ми(перпендикул-ми),
если угол между ними равен 90˚. И далее
в учебнике идет: Если прямая а
перпендикулярна прямой b,
то
пишут
а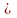 b
и читают: «Прямая а
перпендикулярна прямой b».
Важно отметить, что из опр. следует, что
перпенд-ые прямые могут пересекаться,
а могут быть скрещивающимися.
b
и читают: «Прямая а
перпендикулярна прямой b».
Важно отметить, что из опр. следует, что
перпенд-ые прямые могут пересекаться,
а могут быть скрещивающимися.
Методика изучения перпендикулярности прямой и плоскости.
Если 2 прямые перп-ны одной пл-ти,то они паралл-ны.
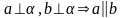
Признак:
Если прямая перп-на 2-ум пересекающимся прямым, лежащим в пл-ти, то она перп-на этой пл-ти.
Подвести к формулировке можно, задав вопросы уч-кам о способах задания пл-ти (если анализировать df и вспомнить, чем отлич-ся признак, то достаточно вспомнить задание пл-ти с помощью 2-х перес-ся прямых).
С
помощью стереометр-ого ящика подвести
к необходимости рассм-ния 2-х случаев:
прямая проходит через точку пересечения
прямых лежащих в пл-ти и не проходит
(проводим прямую
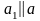 через точку пересечения, тогда
через точку пересечения, тогда
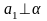 ).
).
Д-во признака явл. одним из наиболее сложных, поэтому:
Иметь каркасную модель
Подготовить таблицу
Компьютерная анимация с последующим показом готового рисунка на доске или таблице.
Дополнительные построения должен подсказать учитель. Последующий поиск док-ва по след.схеме:
1)OL–медиана
треуг-каABL,
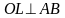 ,
если тр-кABL–равнобедр,т.е.AL=BL
– ?
,
если тр-кABL–равнобедр,т.е.AL=BL
– ?
2)
 –
?
–
?
PL-общая,
AP=B,
сл-но
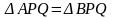 (по
3-м сторонам)
(по
3-м сторонам)
AQ=BQ,сл-но
 (по
2-м катетам).
(по
2-м катетам).
Док-во запис-ся в обратном порядке и может быть предложен след.план:
AP=BP, AQ=BQ
(по 3-м сторонам),
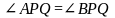
(по 2-м сторонам и углу), AL=BL
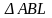 –равнобедр.,т.к.AL=LB,LO-медиана,сл-но
LO-высота,
.
–равнобедр.,т.к.AL=LB,LO-медиана,сл-но
LO-высота,
.
Для док-ва многих утв-ний в данной теме исп-ся теоремы о сущ-нии и ед-ти пл-ти перп-ной данной прямой и обратная ей.
Методика изучения перпендикулярности плоскостей.
В процессе введения понятия перпендикулярности плоскостей необходимо использовать наглядность из окружающей обстановки, модели многогранников (куба, прямоугольного параллелепипеда, прямой призмы).
С учащимися в процессе изучения перпендикулярности плоскостей отрабатываются вопросы:
Определение перпендикулярных плоскостей (Две плоскости называются перпендикулярными, если угол между ними равен 900);
Признак перпендикулярности плоскостей и его доказательство (Если одна из плоскостей проходит ч/з прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны);
Построение перпендикулярных плоскостей;
Решение задач с использованием определения и признака перпендикулярности плоскостей.
Вопрос
существования перпендикулярных
плоскостей может быть решен сразу после
их определения. Для этого можно решить
задачу: прямая а
не
перпендикулярна плоскости
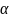 .
Доказать, что существует плоскость,
проходящая ч/з прямую а
и перпендикулярна плоскости
.
.
Доказать, что существует плоскость,
проходящая ч/з прямую а
и перпендикулярна плоскости
.
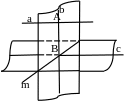 Дано:
Дано:
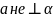
Доказать:
существует
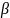 :
:

Доказательство:
Выберем произвольную точку
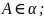
Проведем ч/з точку A прямую b, перпендикулярную плоскости
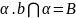
Рассмотрим плоскость , заданную пересекающимися прямыми
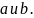
Плоскости
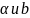 имеют общую точку B,
значит, пересекаются по прямой m,
проходящей ч/з точку B.
имеют общую точку B,
значит, пересекаются по прямой m,
проходящей ч/з точку B.
Докажем, что
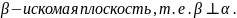
Для
этого в плоскости
ч/з точку B
проведем прямую С перпендикулярно
прямой m
пересечения плоскостей
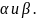 Так как b
Так как b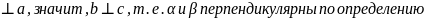 .
.
Вопрос о единственности плоскости можно предложить для самостоятельного рассмотрения.
Решение этой задачи после определения перпендикулярных плоскостей позволит отработать его ,так как доказательство сводится к определению и будет хорошей подготовкой к доказательству признака перпендикулярности двух плоскостей.
