27.Методика изучения рациональных чисел и действий над ними.

Тема изучается в 6 классе после изучения десятичных дробей.

Вспомнить какие числа уже известны. Сказать, что все числа кот. Уже изучили, кроме 0, называются положительными. Перед ними можно поставить знак +.

Мотивация: (практическая)показать термометр, спросить какую температуру он показывает. Называют. Для записи температуры ниже нуля необходимы новые числа – числа со знаком – . показать температуру ниже нуля.

Сделать вывод, что если перед положительным числом поставить знак минус,то получится новое число, которое называется отрицательным числом.

Обратить внимание на то, то число 0 не является ни отрицательным, ни положительным.

Любое положительное число записывают дробью m/n где m,n нат. исла. Любое положительное число записывается дробью со знаком -.

Положит. дроби, отрицательные и нуль называются рациональными числами.

Методы: объяснительно – иллюстративный.

Средства: термометр.

35 Методика изучения показательной и логарифмической функции.

Актуализация знаний учащихся по теме, кот. непоср. изучалась при введений степ. фун., степени с рациональным показателем, её свойства, степ. с действительным показателем. В систему упражнений включит следующие:

-сравнить степени с одним основанием

-подвести что каждому t, ставится одно знач. , следовательно задана функция y=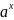 , a>0.

Затем обсудить название функции: Переменная в показатели степени => показательная. Потом уточнить знач. входящих эл-тов, оговорить случай а=0, добавить к определению а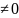 и сформулировать определение.

Опр. Функция, заданая формулой y= при a>0, а называют показательной.

Обл. определения показательной функции – это математическая обл. определения выражения , т. е. R.

Далее следует построить график на доске.

Мотивацию изучения данной темы можно ввести на любом моменте урока, различными примерами: - зависимость популяций сов определяется по закону y=y

• атмосферное давление измер по закону p= 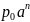и т. д.

Затем составить таблицу значений фун-ций y= и y=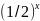 а ученики строят рис. в тетрадях

Введение логарифмической функции:

Вводится понятие обратной функции;

фун., обратная показательной y= , a>0, а называется логарифмической, и задаётся формулой: y=log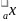

Мотивация введения логарифма явл. след. факторы:

- необходимость решения уравнения b= ,

Доказать что уравнение имеет один корень, можно показать при помощи рисунка.

здесь удобно пояснить что как и в уравнении b= ,так и в записи логарифма a – основание, a>0 , a 1,b значение степени , b>0

при таком подходе легко вывести основные логарифмические тождества.

, b= .

36. Методика изуч. Производной и её применение

В науке производная определяется через понятие предела ф-и, а именно y’=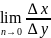

В школе вводится следующее определение производной:

Производной y’=f(x) в т. , называется число, к которому стремится отн. , при 0. Цель изучения в школе – рассмотрение еще одного класса ф-ций и их простейших приложений, закрепление общей схемы исследования функций.

Требуется предварительное определение понятий: 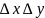, , окрестность т x, интервал.

Для записи изменения вводится значок . Разность x- =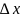 – приращение аргумента в т. ,

X= +

f(x)-f( )= (*)– приращение функции

Нужно обратить внимание , что (*) задаёт функцию, необходимо показать ученикам геом. Смысл приращений 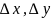на графике произвольной функции. Обратить внимание что . Символ пояснить как: разность между x- становиться всё меньше, и близкая к нуль то x-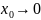 или 0

Далее учителю лучше рассмотреть пример нахождения приращения: . Лучше сразу формировать алгоритм нахождения y’:

1. Выберем множ. т. . Придадим приращение

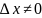
2.

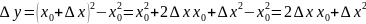
3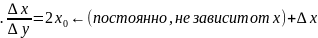

4. 0, то – число наз. производной ф-ии

Вводим определение, затем обозначаем для данного примера f’( )=2 , а затем материал обобщаем.

Пусть y=f(x) имеет произв. В заданной т. некоторого промежутка, тогда каждому числу x соотв. одно опр. знач. f’(x), т.о. получается новая функция , которая наз. производной.

y=f(x) явл. функцией. Поскольку эта функция произведена, то она получила название производной.

С помощью алгоритма ученикам можно показать, что производная может и не существовать.

Перед изуч. учитель должен выполнить с учен-ми опр. ср. скорости, опр. касательной и его угловой коэффициент к граф фун.

Цели: показать практическую значимость производной, но авторы ограничиваются применением производной к иссл. функций, причём внимание уделяется след. вопросам:

1. Убывание и возрос. ф. 2. мак. и мин. фун.3. Особенности изуч. возр. и убыв.:-не вводится термина монотонности; -возр. и убыв. вводятся без доказательства; -используется строгое неравенство f(x)>0 и f(x)<0;