3.1 Решение систем линейных алгебраических уравнений методом Гаусса

В электроэнергетических задачах наибольшее распространение получил метод последовательных исключений Гаусса. Он относится к классу точных методов решения систем линейных алгебраических уравнений. Процесс решения по методу Гаусса состоит из двух этапов: прямой ход метода и обратный ход. На первом этапе (прямой ход) система приводится к треугольному виду, на втором этапе (обратный ход) идет последовательное определение неизвестных из этой треугольной системы.

Пусть дана система линейных алгебраических уравнений п - го порядка.

Будем считать, что коэффициент , который называют ведущим элементом первого шага, отличен от нуля (в случае, если =0, нужно поменять местами первое уравнение с i-тым уравнением, в котором 0). Разделим теперь почленно первое уравнение системы на коэффициент . Введем множители:

Прибавим теперь к каждому i- тому уравнению системы первое уравнение, умноженное на m_i1. Проделав эту операцию, мы исключим неизвестное x₁, из всех уравнений, начиная со второго. Преобразованная система примет вид:

Здесь индекс (1) означает новые значения коэффициентов и правых частей, которые получаются после выполнения первого шага прямого хода метода Гаусса.

Переходя, к выполнению второго шага прямого хода метода Гаусса предположим, что элемент , который называют ведущим элементом второго шага, не равен нулю. Разделим второе уравнение на коэффициент . Введем множители:

Прибавим к i-тому уравнению системы (3), второе уравнение, умноженное на т_i2, в результате исключим неизвестное x₂ из всех уравнений, кроме первых двух.

Проведя далее аналогичные преобразования, после n-го шага придем к треугольной системе вида :

Второй этап - обратный ход метода Гаусса реализуется следующим образом. Из последнего уравнения системы (4) определяем х_n. По найденному значению х_n из n-го уравнения определяем неизвестное x_(n-1). Затем по значениям х_n и x_(n-1) из (n-2)- го уравнения находим x_(n-2) и т.д.

Последовательное вычисление неизвестных продолжается до тех пор, пока из первого уравнения системы (4) не определим . На этом процесс решения заканчивается.

3.2 Решение систем линейных алгебраических уравнений в системе matlab Решение систем линейных алгебраических уравнений методом Жордана-Гаусса

Метод Жордана - Гаусса является одной из модификаций метода Гаусса, в котором матрица коэффициентов при неизвестных последовательно приводится к единичной матрице, а на месте столбца свободных членов в расширенной матрице в результате располагается решение системы линейных алгебраических уравнений:

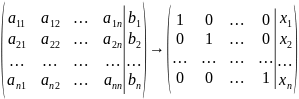
Сущность этого метода заключается в том, что, начиная со второго шага, зануляются все элементы в соответствующем столбце, кроме элемента, стоящего на главной диагонали. Это достигается с помощью алгебраических преобразований аналогичных классическому методу Гаусса. Если имеется система линейных алгебраических уравнений n-го порядка, то на каждом шаге прямого хода метода Гаусса в каждом столбце матрицы коэффициентов зануляется ровно (n-1) коэффициент.

Стандартной функцией, которая реализует метод Жордана-Гаусса в системе MATLAB , является функция rref(). Аргументом у этой функции является расширенная матрица коэффициентов.

Для решения систем линейных алгебраических уравнений с помощью MATLAB можно применять оператор «\», который самостоятельно выбирает лучший метод для решения заданной системы уравнений. При этом решение системы линейных алгебраических уравнений любого порядка достигается одной командой:

»Х =(А\В)’