Решение дифференциальных уравнений
Содержание
Задача
1. Найти
общий интеграл дифференциального
уравнения. (Ответ представить в виде
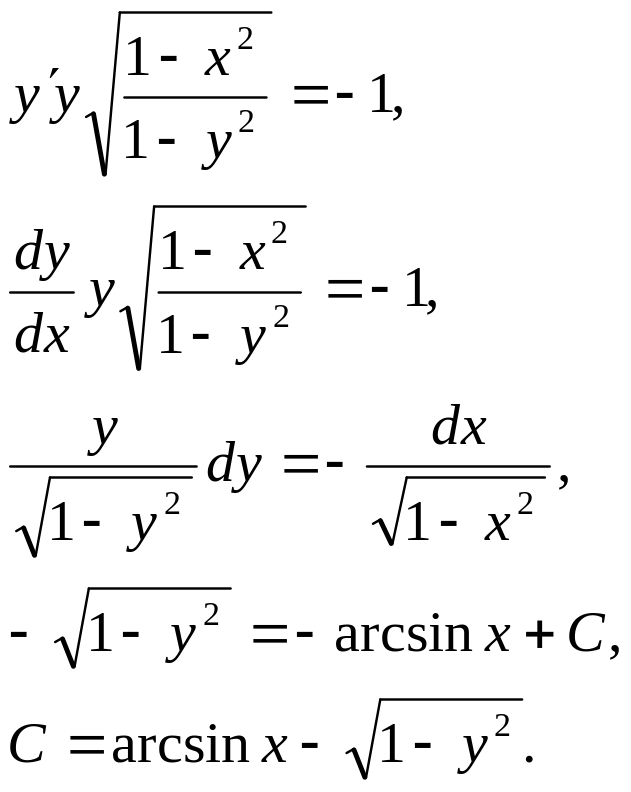
Задача 2. Найти общий интеграл дифференциального уравнения.
Введем
замену
Задача 3. Найти общий интеграл дифференциального уравнения.
Пусть
Введем
замену
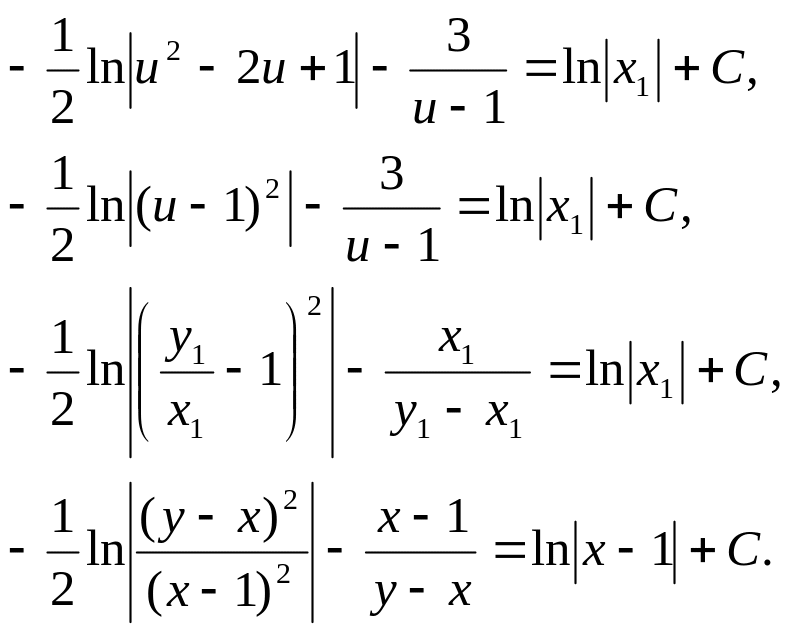
Задача 4. Найти решение задачи Коши.
,
Пусть
Разделим
переменные в этом дифференциальном
уравнении относительно функции
,
находим
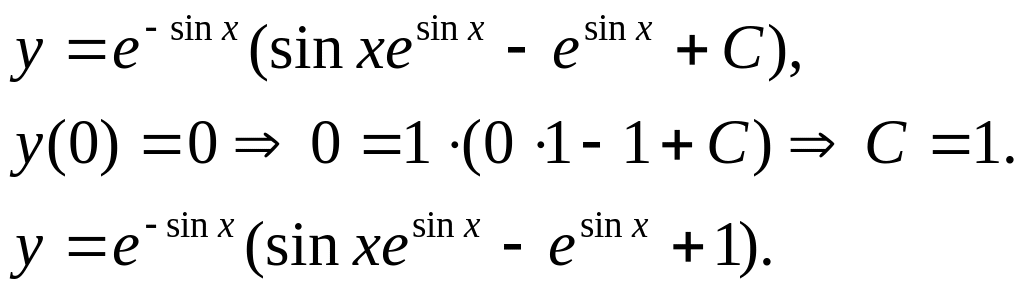
Задача 5. Решить задачу Коши.
Пусть
Разделим переменные в этом дифференциальном уравнении относительно функции , находим
1)
2)
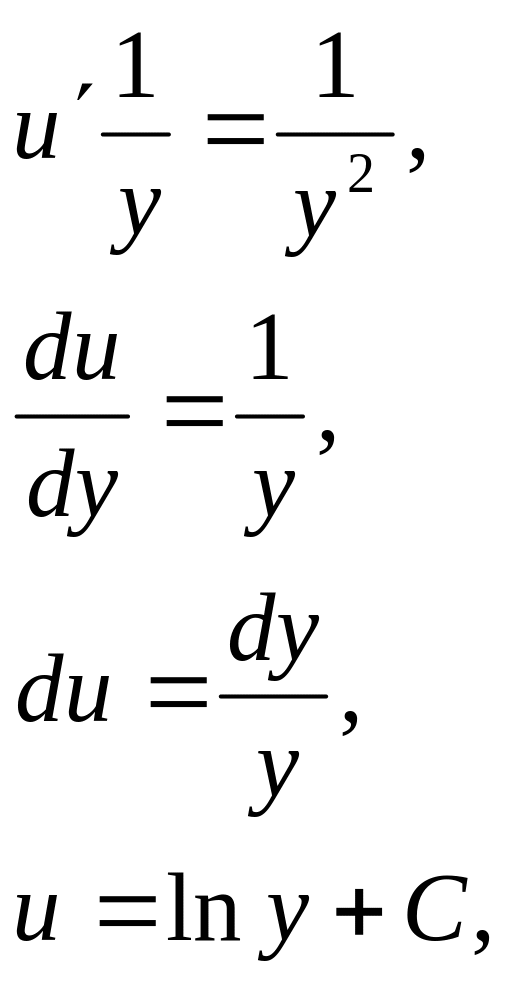
-общее
решение ДУ.
-частное
решение ДУ.
Задача 6. Найти решение задачи Коши.
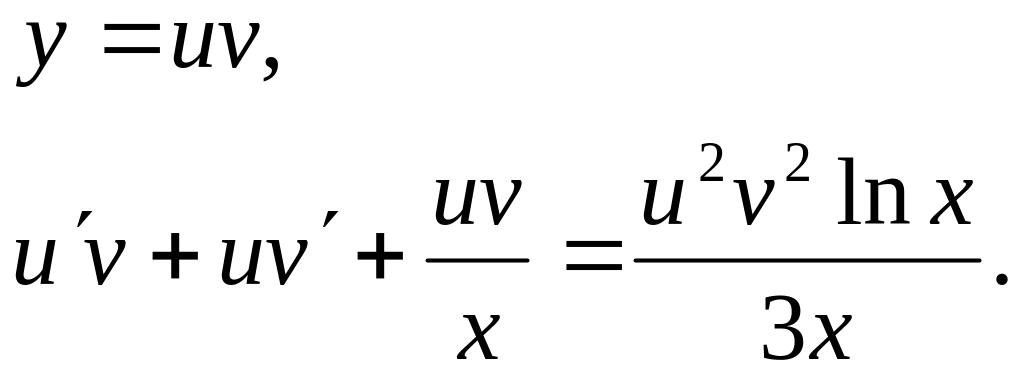
1)
Пусть
2)
Задача 7. Найти общий интеграл дифференциального уравнения.
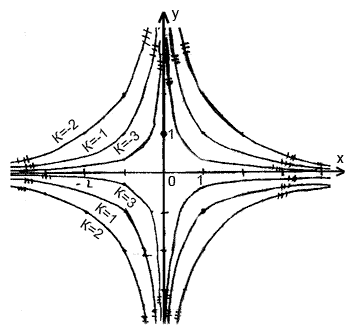
Задача 8. Для данного дифференциального уравнения методом изоклин построить интегральную кривую, проходящую через точку.
т.е.
гипербола.
Задача
9. Найти
линию, проходящую через точку
,
если отрезок любой ее касательной между
точкой касания и осью
делится
на точке пересечения с осью абсцисс в
отношении
(считая от оси
).
уравнение
касательной.
-координаты
произвольной точки, принадлежащие
касательной.
По условию
и
подобны.
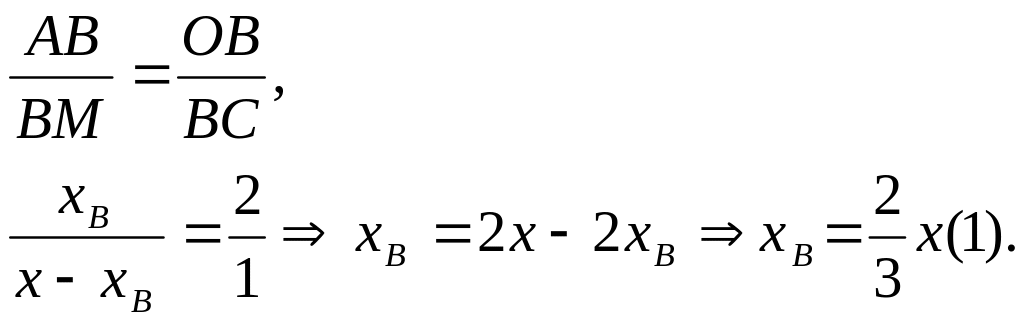
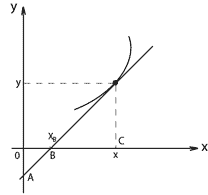
Точка
принадлежит
касательной, поэтому подставим координаты
координаты точки
в
уравнение касательной.
Подставим (1) в (2).
Отсюда,
уравнение
искомой линии.
Задача 10. Найти общее решение дифференциального уравнения.
Замена:
Предположим,
что
Пусть
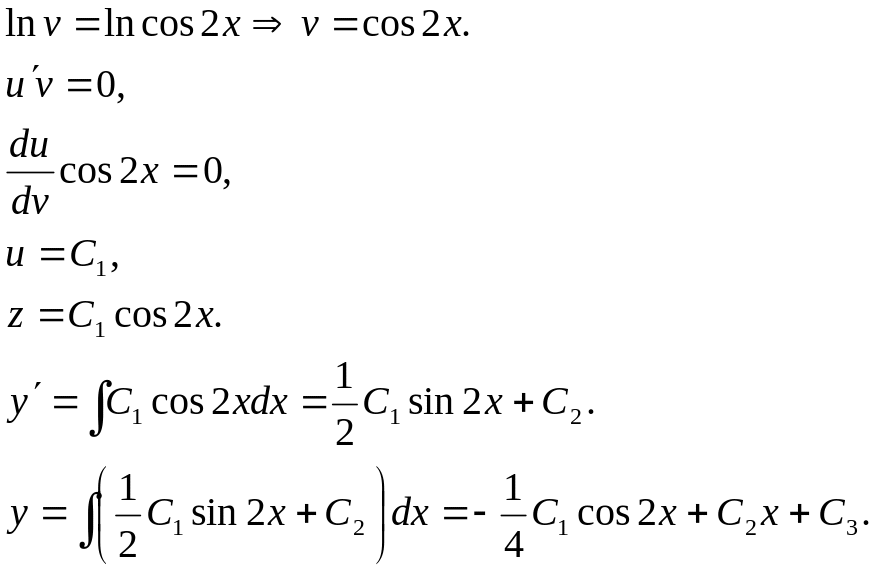
Задача 11. Найти решение задачи Коши.
Замена:
,
Задача 12. Найти общее решение дифференциального уравнения.
-характеристическое
уравнение.
-общее
решение однородного уравнения.
Отсюда
-
частное решение неоднородного уравнения.
Общее решение
Задача 13. Найти общее решение дифференциального уравнения.
-характеристическое
уравнение.
-общее
решение однородного уравнения.
Отсюда
-
частное решение неоднородного уравнения.
Общее решение
Задача 14. Найти общее решение дифференциального уравнения.
-характеристическое
уравнение.
-общее
решение однородного уравнения.
Отсюда
-
частное решение неоднородного уравнения.
Общее решение
Задача 15. Найти общее решение дифференциального уравнения.
-характеристическое уравнение.
-общее решение однородного уравнения.
Отсюда
-
частное решение неоднородного уравнения.
Общее решение
Задача 16. Найти решение задачи Коши.
-характеристическое
уравнение.
-общее
решение однородного уравнения.
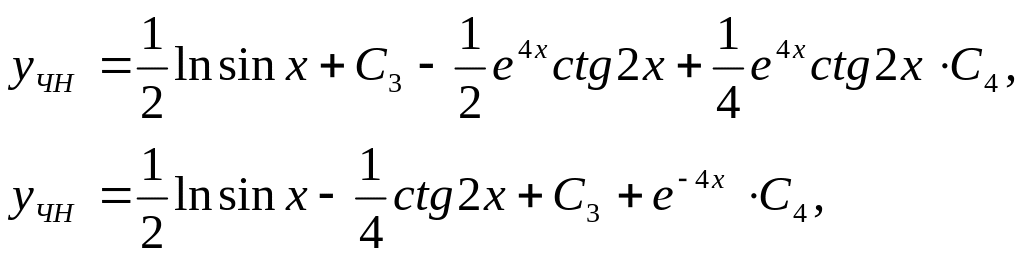
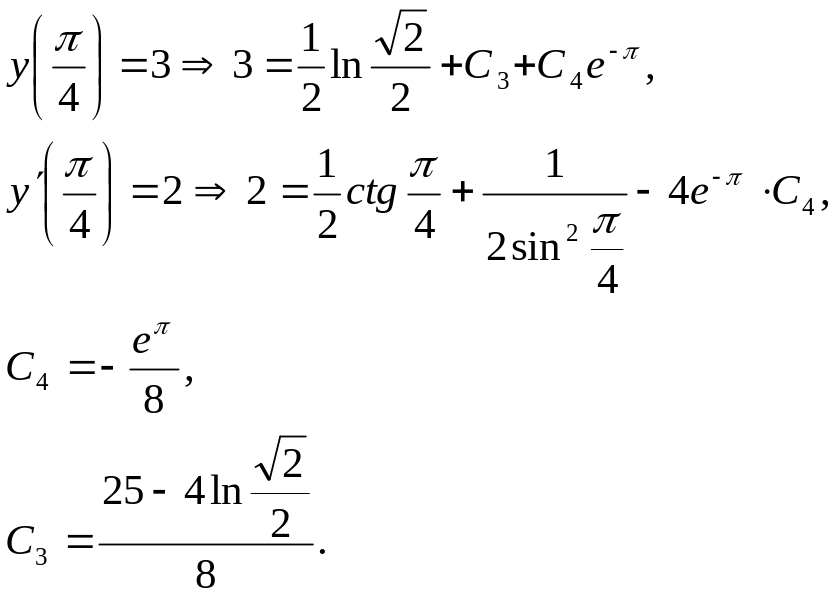
Общее решение
ЗАДАЧИ
Содержание
Теоретические вопросы
Основные понятия теории дифференциальных уравнений. Задача Коши для дифференциального уравнения первого порядка. Формулировка теоремы существования и единственности решения задачи Коши.
Дифференциальные уравнения первого порядка: с разделяющимися переменными, однородные и приводящиеся к ним.
Линейные уравнения первого порядка, уравнение Бернулли.
Уравнения в полных дифференциалах.
Приближенное интегрирование дифференциальных уравнений первого порядка методом изоклин.
Дифференциальные уравнения высших порядков. Задача Коши. Формулировка теоремы существования и единственности решения задачи Коши. Общее и частное решения. Общий и частный интегралы.
Дифференциальные уравнения, допускающие понижение порядка.
Линейный дифференциальный оператор, его свойства. Линейное однородное дифференциальное уравнение, свойства его решений.
Линейно-зависимые и линейно-независимые системы функций. Необходимое условие линейной зависимости системы функций.
Условие линейной независимости решений линейного однородного дифференциального уравнения.
Линейное однородное дифференциальное уравнение. Фундаментальная система решений. Структура общего решения.
Линейное неоднородное дифференциальное уравнение. Структура общего решения.
Метод Лагранжа вариации произвольных постоянных.
Линейные однородные дифференциальные уравнения с постоянными коэффициентами (случай простых корней характеристического уравнения).
Линейные однородные дифференциальные уравнении с постоянными коэффициентами (случай кратных корней характеристического уравнения).
Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами. Метод подбора.