Теорема о кинетической энергии материальной точки

Кинетическая энергия материальной точки выражается половиной произведения массы этой точки на квадрат ее скорости.

Теорему о кинетической энергии материальной точки можно выразить в трех видах:

(187)

т. е. дифференциал кинетической энергии материальной точки равен элементарной работе силы, действующей на эту точку;

т. е. производная по времени от кинетической энергии материальной точки равна мощности силы, действующей на эту точку:

т. е. изменение кинетической энергии материальной точки на конечном пути   равно работе силы, действующей на точку на том же пути.

 

9.Общие теоремы динамики. Количество движения, импульс силы. Закон об изменении количества движения.

Общие теоремы динамики

Количеством движения материальной точки называется векторная величина, равная произведению массы точки на ее скорость  Вектор количества движения совпадает по направлению с вектором скорости. Единица измерения  Произведение постоянного вектора силы на некоторый промежуток времени, в течение которого действует эта сила, называется импульсом, силы Ft. Вектор импульса силы по направлению совпадает с вектором силы. [Ft] = Н • с = кг • м/с.

Количество Движения - мера механического движения, равная для материальнойточки произведению ее массы m на скорость v. Количество движения mv -величина векторная, направленная так же, как скорость точки. Количестводвижения называется также импульсом. 

Импульс силы. Покой и движение тела относительны, скорость движения тела зависит от выбора системы отсчета. По второму закону Ньютона независимо от того, находилось ли тело в покое или двигалось, изменение скорости его движения может происходить только при действии силы, т.е. в результате взаимодействия с другими телами.

Если на тело массой m в течение времени t действует сила F и скорость его движения изменяется от V₀ до V, то ускорение a движения тела равно 

На основании второго закона Ньютона для силы F можно написать выражение 

Из этого равенства следует, что 

Из доказанного равенства можно сделать вывод, что физическая величина, равная произведению силы F на время t ее действия, называется импульсом силы.

Теорема об изменении количества движения

Рассматривается произвольная механическая система, состоящая из материальных точек   движущаяся под действием приложенных сил относительно некоторой инерциальной системы координат Oxyz. Если система несвободна, мысленно освобождаемся от связей, добавляя к задаваемым (активным) силам реакции связей. После этого все действующие силы (активные и реакции связей) разделяем на внешние и внутренние. Тогда равнодействующие   сил, приложенных к точкам системы, будут складываться из внешней и внутренней сил:

Запишем выражение для количества движения системы

и продифференцируем по времени обе части написанного равенства:

Далее преобразуем последний член этого равенства, используя основное уравнение динамики и равенство нулю главного вектора внутренних сил:

В результате для производной количества движения получаем

Полученное равенство в математической форме выражает теорему об изменении количества движения механической системы: производная по времени от количества движения механической системы равна главному вектору всех внешних сил.

Проектируя это векторное равенство на координатные оси Oxyz, получаем математическое выражение теоремы в скалярной форме:

В этих формулах

— проекции количества движения системы на координатные оси, а

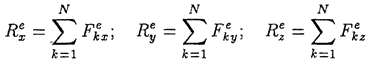
— проекции на эти же оси главного вектора внешних сил.

10. Уравнение динамики для вращающегося тела.

  Выведем уравнение динамики вращательного движения тела. Из выражений (4.1), (4.2) и (4.3) следует, что скорость изменения момента импульса i-й материальной точки определяется следующим образом:                                                                            (4.6)       Сложим почленно уравнения (4.6), записанные для каждой из материальных точек тела: 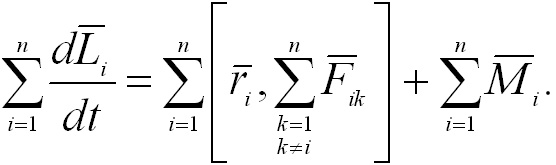                                                            (4.7)       Векторная сумма моментов M_i всех внешних сил, приложенных к телу, называется результирующим, или главным, моментом M внешних сил относительно точки О:

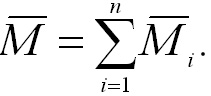
      Векторная сумма моментов импульса L_i всех материальных точек тела называется моментом импульса L телаотносительно точки О:

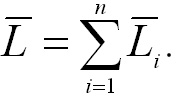
      Так как производная от суммы равна сумме производных от всех слагаемых, то

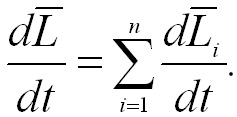
      Наконец, векторная сумма моментов относительно точки О всех внутренних сил F_ik взаимодействия между точками тела равна нулю, т.е.

т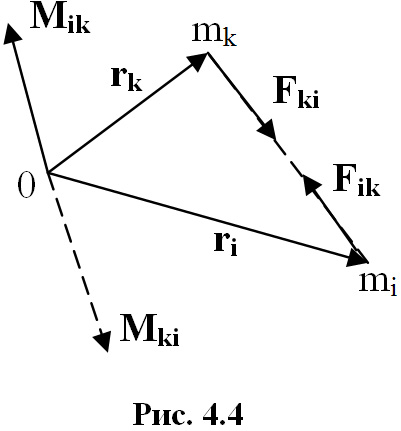 ак как по третьему закону Ньютона силы F_ik и F_ki численно равны, имеют общую линию действия, но направлены в противоположные стороны (рис. 4.4). Поэтому их моменты M_ik = [r_i, F_ik] и M_ki = [r_k, F_ki] относительно точки О численно равны и противоположны по направлению (на рис. 4.4 точки m_i, m_k и О лежат в горизонтальной плоскости, а векторы M_ik и M_ki перпендикулярны этой плоскости). Действительно, r_k = r_i + r_ki, где r_ki - вектор, проведенный из точки m_i в точку m_k. Поэтому M_ki = [r_k, F_ki] + [r_ki, F_ki] = -[r_i, F_ik] = -M_ik, так как векторное произведение векторов r_ki иF_ki, направленных вдоль одной прямой, равно нулю.       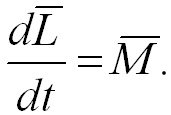На основании изложенного уравнение (4.7) можно записать в следующем виде:                                                                                                     (4.8)       Таким образом, скорость изменения момента импульса тела, вращающегося вокруг неподвижной точки, равна результирующему моменту относительно этой точки всех внешних сил, приложенных к телу.       Полученный результат называется основным законом динамики вращательного движения тела, закрепленного в одной неподвижной точке. Момент импульса является основной динамической характеристикой твердого тела, вращающегося вокруг неподвижной точки.

11.Трение(понятие трения, классификация, краткая характеристика видов трения).

Трение — сопротивление, возникающее при движении одного шероховатого тела по поверхности другого. При скольжении тел возникает трение скольжения, при качении — трение качения. Природа сопротивлений движению в разных случаях различна.

Трение скольжения

Причина — механическое зацепление выступов. Сила сопротивления движению при скольжении называется силой трения скольжения (рис. 13.3а).

Законы трения скольжения:

1. Сила трения скольжения прямо пропорциональна силе нормального давления:

Fтр = Ff = f R,

где R — сила нормального давления, направлена перпендикулярно опорной поверхности;

f — коэффициент трения скольжения.

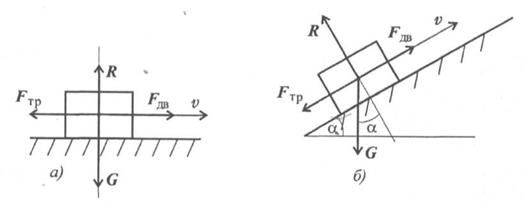
Рис.

В случае движения тела по наклонной плоскости (рис. 13.36)

R = G cos α,

где а — угол наклона плоскости к горизонту.

Сила трения всегда направлена в сторону, обратную направлению движения.

2. Сила трения меняется от нуля до некоторого максимального значения, называемого силой трения покоя (статическое трение):

0 < Ff ≤ Ff0,

где Ff0 — статическая сила трения (сила трения покоя).

3.  Сила трения при движении меньше силы трения покоя. Сила трения при движении называется динамической силой трения (Ff):

Ff ≤ Ff0,

Поскольку сила нормального давления, зависящая от веса и направления опорной поверхности, не меняется, то различают статический и динамический коэффициенты трения:

Ff  = f R, Ff0 = ff0R.

Коэффициент трения скольжения зависит от следующих факторов:

— от материала: материалы делятся на фрикционные (с большим коэффициентом трения) и антифрикционные (с малым коэффициентом трения), например f = 0,l ÷ 0,15 (при скольжении стали по стали всухую), f = 0,2 ÷ 0,3 (при скольжении стали по текстолиту);

от наличия смазки, например f = 0,04 ÷ 0,05 (при скольжении стали по стали со смазкой);

от скорости взаимного перемещения.

Трение качения

Сопротивление при качении связано с взаимной деформацией грунта и колеса и значительно меньше трения скольжения.

Обычно считают грунт мягче колеса, тогда в основном деформируется грунт, и в каждый момент колесо должно перекатываться через выступ грунта. Для равномерного качения колеса необходимо прикладывать силу FnB (рис. 13.4).

Условие качения колеса состоит в том, что движущийся момент должен быть не меньше момента сопротивления: Fдв r ≥ N k; N = G;  где k – максимальное значение плеча (половина колеи) принимаемая за коэффициент трения качения, размерность – сантиметры. Ориентировочные значения k (определяются экспериментально): сталь по стали – k=0,005 см; резиновая шина по шоссе – k=0,24 см.