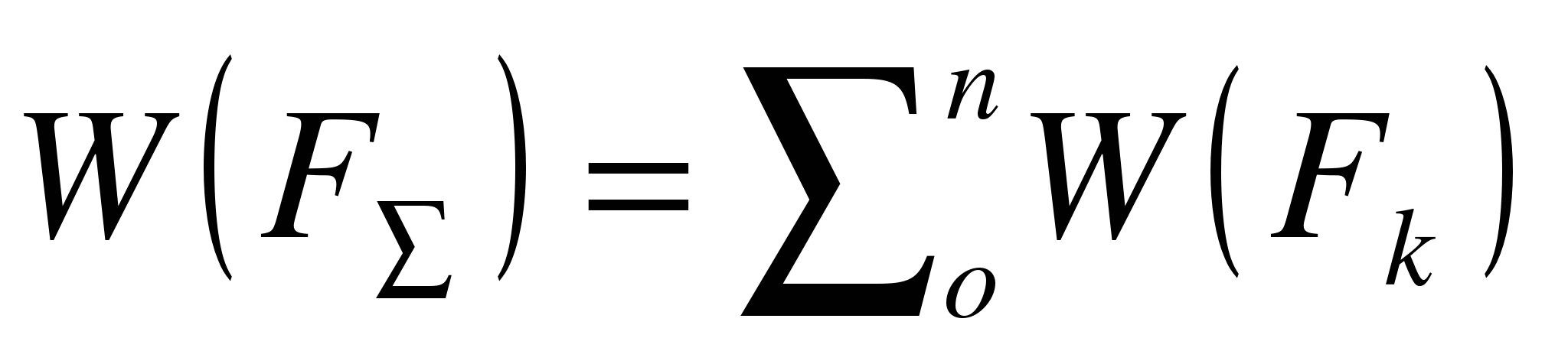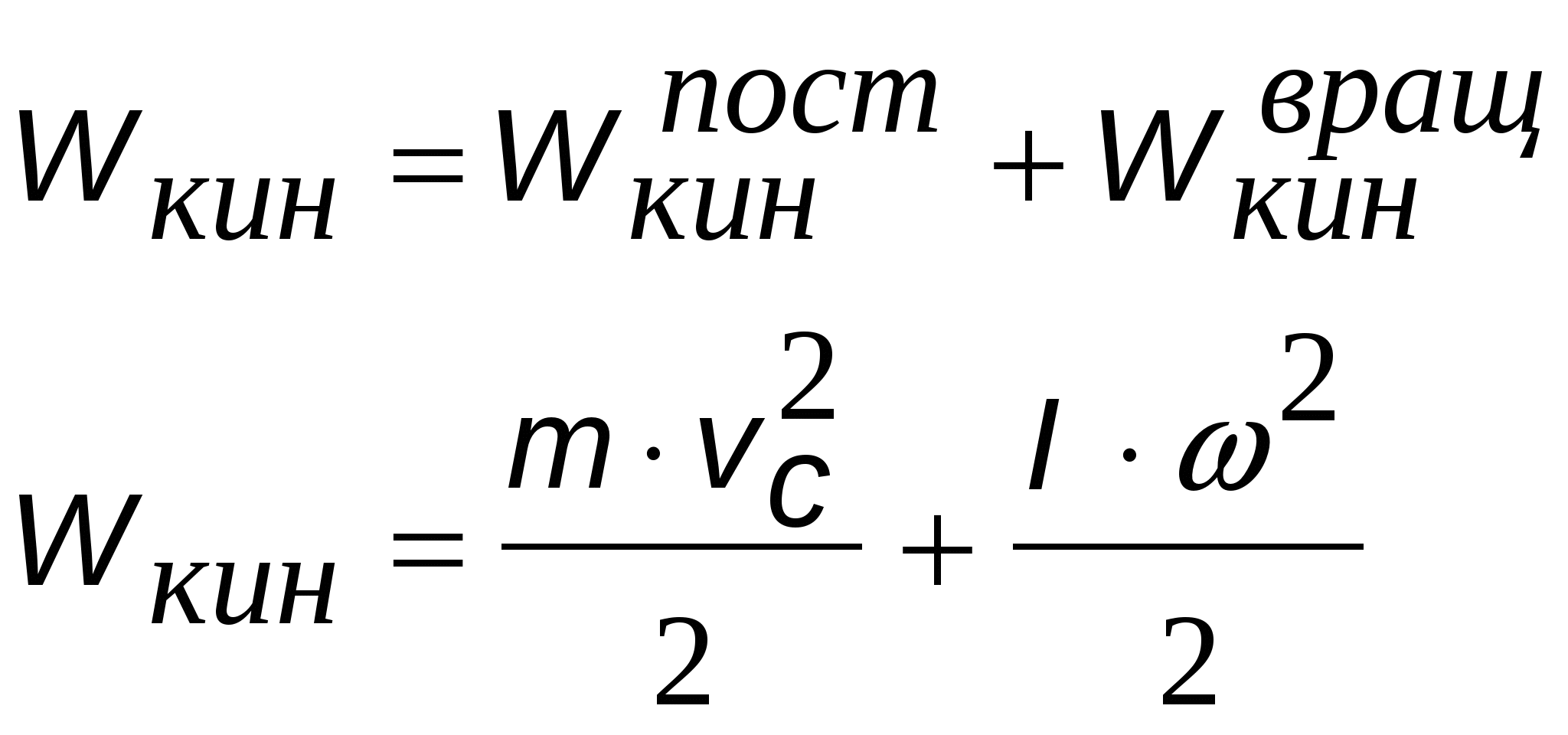- •Скорость точки при векторном способе задания движения.
- •Определение скорости при координатном способе задания движения.
- •Нахождение скорости при естественном способе задания движения.
- •Принцип Даламбера для материальной точки
- •Теорема о кинетической энергии материальной точки
- •Общие теоремы динамики
- •Теорема об изменении количества движения
Принцип Даламбера для материальной точки
Пусть
материальная точка массы ![]() совершает
несвободное движение относительно
инерциальной системы координат Oxyz под
действием активной силы
совершает
несвободное движение относительно
инерциальной системы координат Oxyz под
действием активной силы ![]() и
реакции связи R (рис. 57).
и
реакции связи R (рис. 57).
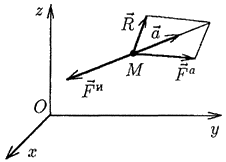
Рис. 57.
Определим вектор
![]()
численно
равный произведению массы точки на ее
ускорение и направленный противоположно
вектору ускорения. Вектор ![]() имеет
размерность силы и называется силой
инерции (даламберовой) материальной
точки.
имеет
размерность силы и называется силой
инерции (даламберовой) материальной
точки.
Принцип Даламбера для материальной точки сводится к следующему утверждению: если к силам, действующим на материальную точку, условно присоединить силу инерции точки, то получим уравновешенную систему сил, т. е.
![]()
Вспоминая из статики условие равновесия сходящихся сил, принцип Даламбера можем записать также в следующей форме:
![]()
Легко
видеть, что принцип Даламбера эквивалентен
основному уравнению динамики, и наоборот,
из основного уравнения динамики следует
принцип Даламбера. Действительно,
перенося в последнем равенстве вектор ![]() в
другую часть равенства и заменяя
в
другую часть равенства и заменяя ![]() на
на ![]() ,
получаем основное уравнение динамики.
Наоборот, перенося в основном уравнении
динамики член та в одну сторону с силами
и используя обозначение
,
получаем основное уравнение динамики.
Наоборот, перенося в основном уравнении
динамики член та в одну сторону с силами
и используя обозначение ![]() ,
получаем запись принципа Даламбера.
,
получаем запись принципа Даламбера.
Принцип Даламбера для материальной точки, будучи вполне эквивалентным основному закону динамики, выражает этот закон в совершенно иной форме — в форме уравнения статики. Это дает возможность пользоваться при составлении уравнений динамики методами статики, что и называется методом кинетостатики.
Метод кинетостатики особенно удобен при решении первой задачи динамики.
Пример.
Из наивысшей точки гладкого сферического
купола радиуса R соскальзывает материальная
точка М массы ![]() с
пренебрежимо малой начальной скоростью
(рис. 58). Определить, в каком месте точка
сойдет с купола.
с
пренебрежимо малой начальной скоростью
(рис. 58). Определить, в каком месте точка
сойдет с купола.

Рис. 58.
Решение.
Точка будет двигаться по дуге некоторого
меридиана ![]() .
Пусть в некоторый (текущий) момент радиус
ОМ составляет с вертикалью угол
.
Пусть в некоторый (текущий) момент радиус
ОМ составляет с вертикалью угол ![]() .
Раскладывая ускорение точки а на
касательное
.
Раскладывая ускорение точки а на
касательное ![]() )
и нормальное
)
и нормальное ![]() представим
силу инерции точки также в виде суммы
двух составляющих:
представим
силу инерции точки также в виде суммы
двух составляющих:
![]()
Касательная
составляющая силы инерции имеет
модуль ![]() и
направлена противоположно касательному
ускорению, нормальная составляющая —
модуль
и
направлена противоположно касательному
ускорению, нормальная составляющая —
модуль ![]() и
направлена противоположно нормальному
ускорению.
и
направлена противоположно нормальному
ускорению.
Добавляя
эти силы к фактически действующим на
точку активной силе ![]() и
реакции купола N, составляем уравнение
кинетостатики
и
реакции купола N, составляем уравнение
кинетостатики
![]()
Проектируя это векторное уравнение на направления касательной и главной нормали, получаем два уравнения кинетостатики в скалярной форме:
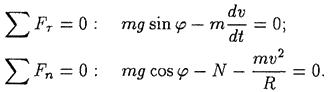
Из второго уравнения находим
![]()
Реакция N окончательно найдется после того, как будет определена величина v и подставлена в это выражение.
Для
определения v служит первое уравнение,
которое является дифференциальным
уравненим и требует интегрирования.
Однако можно избежать интегрирования,
если воспользоваться теоремой об
изменении кинетической энергии. Применяя
эту теорему для точки М на участке
траектории ![]() и
учитывая, что
и
учитывая, что ![]() (работу
совершает только сила тяжести), получаем:
(работу
совершает только сила тяжести), получаем:
![]()
Отсюда находим
![]()
и далее
![]()
В момент отделения от купола реакция N равна нулю. Следовательно, точка сойдет с купола при
![]()
4.Работа постоянной силы на прямолинейном пути. Работа переменной силы на криволинейном пути.
Работа постоянной силы на прямолинейном пути
Работа силы в общем случае численно равна произведению модуля силы на длину пройденного пути и на косинус угла между направлением силы и направлением перемещения (рис. 15.1): W = FS cos α. Единицы измерения работы: 1 Дж (джоуль) = 1 Н-м; 1 кДж (килоджоуль) = 103 Дж. |
|
Рассмотрим частные случаи. 1. Силы, совпадающие с направлением перемещения, называются движущими силами. Направление вектора силы совпадает с направлением перемещения (рис. 15.2). В этом случае α = 0° (cos α = 1). Тогда W = FS > 0. 2. Силы, перпендикулярные направлению перемещения, работы не производят (рис. 15.3).
-
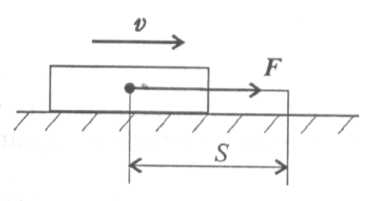 Рис.
Рис. 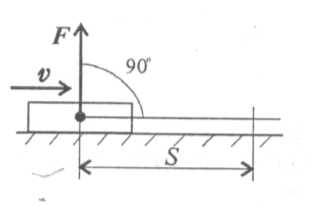 Рис.
Рис.
Сила F перпендикулярна направлению перемещения, а = 90° (cos α = 0); W = 0. 3. Силы, направленные в обратную от направления перемещения сторону, называются силами сопротивления (рис. 15.4).
|
Сила F направлена в обратную от перемещения Sсторону. В этом случае а = 180° (cos α = - 1), следовательно, W= - FS < 0. Движущие силы увеличивают модуль скорости, силы сопротивления уменьшают скорость. |
Таким образом, работа может быть положительной и отрицательной в зависимости от направления силы и скорости.
Работа постоянной силы на криволинейном пути Пусть точка М движется по дуге окружности и сила F составляет некоторый угол а с касательной к окружности (рис. 15.5).
Вектор силы можно разложить на две составляющие: F = Ft + Fn. Используя принцип независимости действия сил, определим работу каждой из составляющих силы отдельно: W (Ft) = Ft ΔŠ ; W (Fn) = Fn ΔŠ , где ΔŠ = М1˘М2 – пройденный путь. ΔŠ = φ r. |
|
Нормальная составляющая силы Fn всегда направлена перпендикулярно перемещению и, следовательно, работы не производит: W(Fn) = 0. При перемещении по дуге обе составляющие силы разворачиваются вместе с точкой М. Таким образом, касательная составляющая силы всегда совпадает по направлению с перемещением. Будем иметь: W(Ft) = Ft φr. Касательную силу Ft обычно называют окружной силой. Работа при криволинейном пути — это работа окружной силы: W(F) = W(Ft ). Произведение окружной силы на радиус называют вращающим моментом: Мвр = Ft r. Работа силы, приложенной к вращающемуся телу, равна произведению вращающего момента на угол поворота: W(F) = Mвр φ.
5.Работа равнодействующей силы. Работа силы тяжести.
Работа равнодействующей силы Под действием системы сил точка массой т перемещается из положения M1 в положение М2 (рис. 15.7). В случае движения под действием системы сил пользуются теоремой о работе равнодействующей. ^ Работа равнодействующей на некотором перемещении равна алгебраической сумме работ системы сил на том же перемещении.
|
FΣ = F1 + F2 + F3 +
… + Fn .
Работа
равнодействующей силы
|
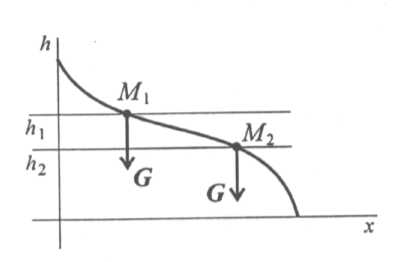
Работа силы тяжести Работа силы тяжести зависит только от изменения высоты ж равна произведению модуля силы тяжести на вертикальное перемещение точки (рис. 15.6): W(G) = G(h1 - h2) = GΔh, где Δh — изменение высоты. При опускании работа положительна, при подъеме отрицательна.
|
6.Работа силы во вращательном движении.
работа при вращательном движении
|
мощность при вращательном движении
Найдем выражение для кинетической энергии при вращении тела относительно неподвижной оси, учитывая, что АТТ - система материальных точек, а энергия аддитивная величина:
|
неподвижной оси
Если тело одновременно движется и поступательно и вращается, то его кинетическая энергия складывается из двух частей:
|
Кинетическая энергия тела при плоском движении
vc – скорость центра масс
Пример. Рассмотрим скатывание сплошного цилиндра с наклонной плоскости.
|
II закон Ньютона в векторном виде для поступательного и вращательного движений. Движение плоское. |
|
|
II закон Ньютона для центра масс в проекциях на оси х и у (оси указаны на рис.) |
|
|
для вращательного движения относительно оси z , проходящей через центр масс С и совпадающей с осью цилиндра – ось направлена перпендикулярно чертежу. R – радиус цилиндра. Силы mg и N момента не создают, т.к. проходят через ось вращения. |
|
|
связь между угловым ускорением и ускорением центра масс аС. |
|
7.Мощность при поступательном и вращательном движениях. Механический КПД.
Мощность: N=A/t, работа равна изменеию потенциальной энергии, в данном случае А=Еп=m*g*S. Время , за которое происходит перемещение на величину S=Vo*t+g*t^2/2, по условию Vo=0, тогда t=sqrt(S*g/2), тогда мощность: N=m*g*S/sqrt(S*g/2)=m*g*sqrt(g*S/2)
МЕХАНИЧЕСКИЙ КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ— отношение работы или мощности на валу машины к работе или мощности, развиваемой в цилиндре машины. М. К. П. Д. характеризует потери энергии на трение в частях машины, передающих движение поршня валу.
8.Механическая энергия(виды). Теорема об изменении кинетической энергии материальной точки.
Если тело может совершить механическую работу, то оно обладает механической энергией Е (Дж). Либо, если внешняя сила совершает работу, воздействуя на тело, его энергия изменяется.
Сучествует два вида механической энергии: кинетическая и потенциальная.
Кинетическая энергия – энергия движущихся тел:
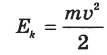
где v (м/с) – модуль скорости, m – масса тела.
Потенциальная энергия – энергия взаимодействующих тел
Примеры потенциальной энергии в механике.
Тело поднято над землей: Е = mgh
где h – высота, определяемая от нулевого уровня (или от нижней точки траектории). Форма траектории не важна, имеет значения только начальна и конечная высота.
Упруго деформированное тело. Деформация, определяемая от положения недеформированного тела (пружины, шнура и т.п.).

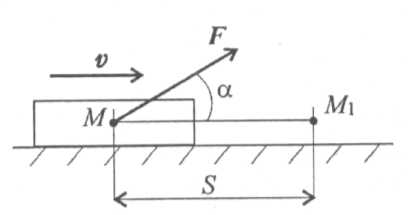 Рис.
Рис. 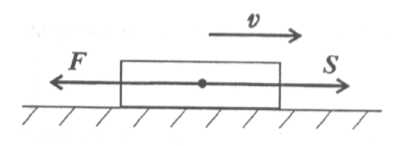 Рис.
Рис. 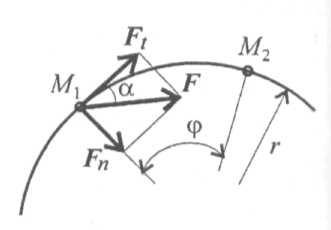 Рис.
Рис. 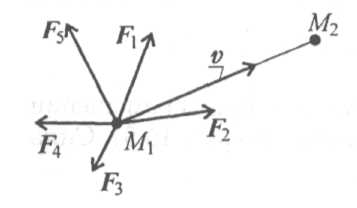 Рис.
Рис.