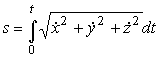Раздел "Кинематика"

1.Предмет и основные понятия кинематики.

Исторически сложилось так, что кинематика, как и статика, развивалась самостоятельно на основе математических наук, в частности, геометрии.

В геометрии введено понятие о пространстве и рассматриваются перемещения точек, описывающих линии, перемещения линий, описывающих поверхности, и т.д., но в ней перемещения никак не связаны со временем.

Если ввести понятие времени, то получится более сложная наука, называемая кинематикой, которая изучает геометрические свойства движения в их отношении со временем, в которой не изучают физических причин движения.

Первичными понятиями кинематики как науки являются понятия пространства и времени, а аксиомами являются аксиомы геометрии, на основе которой построена кинематика.

Напомним, что в теоретической или классической механике пространство подчиняется геометрии Евклида, время одинаково во всех точках пространства и не зависит от движения, а система отсчета содержит только тело отсчета и связанную с ним систему координат. Соответственно, аксиомами кинематики классической механики являются аксиомы геометрии Евклида.

В настоящее время кинематика включена в теоретическую механику как раздел, в котором движение изучается без учета сил, вызвавших движение, и инерционности тел.

К основным задачам кинематики относятся: установление кинематических параметров и определение положения тел в системе отсчета с их помощью; изучение изменения кинематических параметров во времени с целью определения всех кинематических характеристик движения.

В соответствии с основными моделями теоретической механики кинематику разделяют на кинематику материальной точки, кинематику системы материальных точек и кинематику твердого тела.

2.Способы задания движения точки: координатный способ задания движения точки.

 Для задания движения точки можно использовать несколько способов. Мы рассмотрим три основных: 1) векторный, 2) координатный, 3) естественный.

Векторный способ. Положение движущейся точки M относительно тела отсчета O можно определить радиус-вектором точки r, соединяющим тело отсчета и точку (рис. 57).

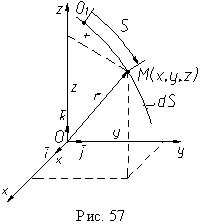
При движении точки M радиус-вектор r будет изменяться по модулю и направлению с течением времени t, то есть

(1)

Выражение (1) определяет закон движения точки и является ее кинематическим уравнением движения в векторной форме.

Конец радиус-вектора совместно с точкой M движется в пространстве по кривой, которая является годографом радиус-вектора, а в кинематике называетсятраекторией точки. Движение точки по кривой называется криволинейным движением точки, если траектория точки - прямая линия, движение точки называетсяпрямолинейным.

То обстоятельство, что радиус-вектор не связан с конкретной системой координат, позволяет широко использовать векторный способ задания движения для теоретических доказательств.

Для решения практических задач обычно используют координатный и естественный способы задания движения.

Координатный способ. Свяжем с телом отсчета систему координат Oxyz. Тогда положение точки M в системе отсчета можно определить тремя координатами точки x, y, z (рис. 57).

При движении точки M ее координаты будут изменяться с течением времени, то есть

x = x(t), y = y(t), z = z(t)

(2)

Выражения (2) определяют закон движения точки и являются ее кинематическими уравнениями в координатной форме.

Уравнения траектории точки можно получить из выражений (2), исключив из них время t. Например, из третьего уравнения в (2) выразим время: t = φ(z). Подставляя время в первые два уравнения, найдем уравнения траектории точки:

x = x(φ(z)), y = y(φ(z))

(3)

С телом отсчета может быть связана не только прямоугольная система координат, но и другие системы координат - сферическая, цилиндрическая и т.д. Так как пространство трехмерное, в этих системах координат положение точки также будет определяться тремя изменяющимися во времени кинематическими параметрами.

Естественный способ. Он используется, когда траектория точки известна. Положение точки на траектории определяется примерно так же, как определяется положение числа на числовой оси.

Для этого нужно задать: 1) начало отсчета O₁; 2) положительное направление отсчета +; тогда положение точки M на траектории будет определяться 3) дуговой координатой s (рис. 57).

При движении точки M по траектории дуговая координата s изменяется с течением времени, то есть

s = s(t)

(4)

Выражение (4) определяет закон движения точки и является ее кинематическим уравнением движения в естественной форме.

Нельзя путать дуговую координату с длиной пути точки. Дуговая координата s может быть положительной, как показано на рис. 57, может быть равна нулю в начале отсчета и может быть отрицательной, когда точка перейдет за начало отсчета.

Путь, пройденный точкой, всегда положителен, так как он равен сумме всех перемещений точки за конечный промежуток времени, и не зависит ни от начала отсчета, ни от направления отсчета. Например, при движении точки по траектории из начала отсчета в положение M и назад дуговая координата точки равна 0, а путь равен 2s.

Связь между способами задания движения точки. Все три способа задания движения точки связаны между собой.

Найдем связь между координатным и векторным способами задания движения. Из математики известно, что координаты точки M являются проекциями ее радиус-вектора на оси системы координат. Записав радиус-вектор в координатной форме, выражаем эту связь:

(5)

где i,j,k являются единичными векторами (ортами) осей координат (рис. 57).

Рассмотрим переход от координатного способа задания движения к естественному. Выделим на траектории точки элементарное дуговое перемещение (дифференциал дуговой координаты)ds (рис. 57). Оно представляет собой диагональ прямоугольного параллелепипеда со сторонами dx, dy, dz, являющимися элементарными приращениями прямоугольных координат (дифференциалами этих координат). Величина диагонали ds равна

(6)

Обозначая производные по времени от координат

(7)

выражаем их дифференциалы: dx = xdt; dy = ydt; dz = zdt. Подставляя последние равенства в выражение (6), получаем

(8)

Предполагая, что при t = 0 точка находится в начале отсчета (s = 0), интегрируя выражение (7) в интервалах от 0 до s и от 0 до t, находим закон движения точки вдоль траектории:

(9)

3.Скорость точки. Движение тела в зависимости от скорости.

Скоростью точки называется кинематический параметр, характеризующий быстроту изменения положения точки в системе отсчета с течением времени.

Скорость точки при векторном способе задания движения.

П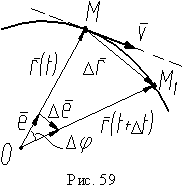 усть движение точки относительно тела отсчета задано ее радиус-вектором r(t). Тогда, по определению, скоростью точки будет векторная производная радиус-вектора r по скалярному аргументу - времени t:

(1)

На рис. 59 изображено как определяется скорость точки. За приращение времени Δt точка переместилась по траектории из положения M в положение M₁, а радиус-вектор получил приращение Δr. Когда Δt   0, точка M₁   M, а вектор Δr, направленный по хорде MM₁, стремится занять положение касательной к траектории. Поэтому вектор скорости V будет направлен, согласно выражению (1), вдоль касательной к траектории в точке M в сторону движения точки.

По определению, вектор скорости является скоростью точки в данное мгновение времени или мгновенной скоростью. Средней скоростью за промежуток времени Δt называется отношение Δr/Δt. Размерность скорости - м/с (метр в секунду), внесистемными единицами скорости могут быть см/с (сантиметр в секунду), км/час (километр в час) и т.д.

Радиальная и трансверсальная скорости. Здесь мы покажем, что скорость, как любая векторная производная по скалярному аргументу, состоит из двух взаимно ортогональных составляющих. Первая из них, направленная по дифференцируемому вектору, характеризует изменение величины вектора, а вторая, перпендикулярная направлению вектора, характеризует изменение направления вектора.

Введем единичный вектор e радиус-вектора r. Тогда радиус-вектор можно записать, как r = re, а скорость точки по формуле (1) будет равна

(2)

Второе слагаемое в выражении (10) содержит производную по времени единичного вектора e. Модуль производной равен

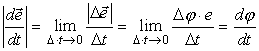
где Δφ - малый угол между r(t) и r(t + Δt) (рис. 59). Там же показано приращение единичного вектора Δe.

Докажем, что производная единичного вектора перпендикулярна самому единичному вектору. Для этого дифференцируем по времени равенство e·e = 1 и получаем, что 2e·e = 1. Так как e <> const, то последнее равенство будет выполняться, когда угол между векторами в скалярном произведении равен pi/2 или когда  . Но e является единичным вектором радиус-вектора, следовательно,  . Введя единичный вектор n, перпендикулярный r и e, выразим производную единичного вектора в виде

(3)

где  . Подставляя формулу (3) в выражение (2), получаем

(4)

где   и  .

Первое слагаемое в выражении (4) обозначим V_R и назовем радиальной скоростью, а второе слагаемое обозначим V_T и назовем трансверсальной скоростью, то есть

(5)

где

(6)

Таким образом, вектор скорости содержит две взаимно перпендикулярные составляющие. Радиальная составляющая, направленная вдоль радиус-вектора, характеризует изменение модуля радиус-вектора с течением времени. Трансверсальная составляющая, перпендикулярная радиус-вектору, характеризует изменение направления радиус-вектора.

Н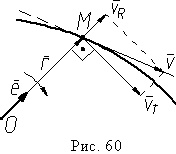 а рис. 60 показано разложение вектора скорости на радиальную и трансверсальную составляющие. Видим, что в данное мгновение времени радиус-вектор увеличивается и поворачивается по часовой стрелке в плоскости, содержащей радиус-вектор и касательную к траектории.

Формулу (4) можно использовать для дифференцирования любого вектора, например, b, по любому скалярному аргументу, например, u. Тогда по формуле (4)

(7)

где e - единичный вектор вектора b, а n - единичный вектор, перпендикулярный e и b. Если величина вектора постоянна, а изменяется только направление вектора, то первое слагаемое в формуле (7) равно нулю и

(8)