
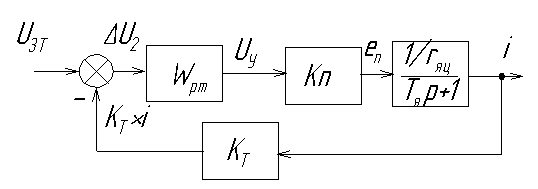
- •1. Упрощенная функциональная схема и принцип действия 2-х контурной системы подчинённого регулирования.
- •2. Сравнительный анализ статических характеристик в схемах с “пи” и “п” регуляторами скорости.
- •12. Позиционный электропривод с линейным регулятором положения, принцип действия, виды перемещений, особенности синтеза и качества переходных процессов
- •13. Основные понятия в электромагнитных процессах: мдс, магнитный поток, потокосцепление, магнитная индукция, индуктивность и индуктивное сопротивление, эдс, наводимые в обмотках.
- •14. Конструктивные особенности и принцип действия асинхронного двигателя.
- •19. Конструктивные особенности двигателя постоянного и переменного тока.
- •20. Принципы регулирования напряжения методом широтно-импульсной модуляции.
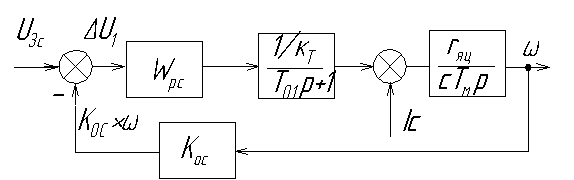
1. Упрощенная функциональная схема и принцип действия 2-х контурной системы подчинённого регулирования.
С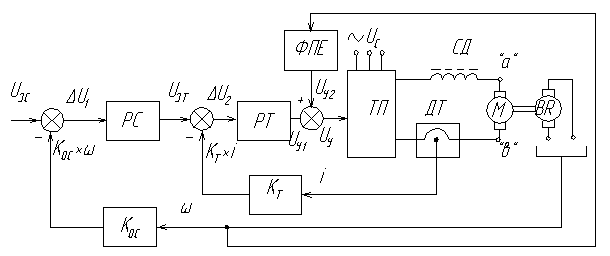 истема
двухконтурная. Внутренний контур
является контуром регулирования тока
якоря с регулятором тока (РТ). Для этого
контура внешним управляющим сигналом
является напряжение заданного тока,
который формируется регулятором тока
РТ. Система построена так, что ТП работает
в режиме источника тока, т.е. в установившемся
режиме ток якоря описывается равенством:
истема
двухконтурная. Внутренний контур
является контуром регулирования тока
якоря с регулятором тока (РТ). Для этого
контура внешним управляющим сигналом
является напряжение заданного тока,
который формируется регулятором тока
РТ. Система построена так, что ТП работает
в режиме источника тока, т.е. в установившемся
режиме ток якоря описывается равенством:
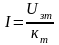 ;
;
Это достигается с помощью ПИ-регулятора тока и с помощью внешнего положения связи по скорости (Э.Д.С.), которая формируется ФПЕ(функциональный преобразователь Э.Д.С.). Внешним контуром является контур скорости с ПИ-регулятором скорости. РС работает в установившемся режиме. В установившемся режиме скорость описывается равенством:
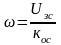 ;
;
Это справедливо лишь, когда регулятор находится в усилительном режиме. При насыщении РС это равенство не справедливо. При анализе сущности протекания процессов удобно представить схему замещения силовой цепи и все специфические особенности.
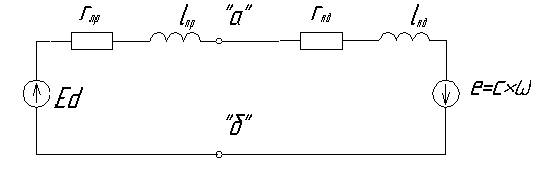
Для удобства
анализа удобно внести следующие
обозначения:
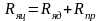 -суммарное
сопротивление якорной цепи;
-суммарное
сопротивление якорной цепи;
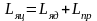 -
суммарная индуктивность якорной цепи;
-
суммарная индуктивность якорной цепи;
Здесь предполагается, что параметры сглаживающего дросселя отнесены к преобразователю.
В установившемся режиме выполняется равенство:
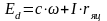 (1);
(1);
Уравнение электромеханической характеристики:
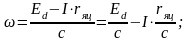 (2)
(2)
Если допустить,
что система разомкнутая (без обратной
связи по скорости и току), т.е.
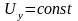 или
или
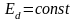 ,
то уравнение прямой.
,
то уравнение прямой.
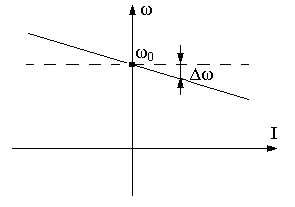
Из принципа
действия (1) следует, что при приложении
нагрузки
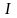 ,
при постоянной
,
при постоянной
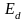 ,
скорость обязательно уменьшится. Причём
падение скорости заключается в появлении
падения напряжения в якорной цепи. В
замкнутой системескорость стабилизируется
с помощью ПИРС, который обладает
оригинальным свойством, если РС находится
в усилительном режиме, то после окончания
переходного, должно выполняться
равенство:
,
скорость обязательно уменьшится. Причём
падение скорости заключается в появлении
падения напряжения в якорной цепи. В
замкнутой системескорость стабилизируется
с помощью ПИРС, который обладает
оригинальным свойством, если РС находится
в усилительном режиме, то после окончания
переходного, должно выполняться
равенство:
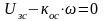 ;
(3)
;
(3)
Отсюда при
работе РС в усилительном режиме
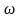 равно:
равно:
;
С учётом этого статические характеристики замкнутой системы характеризуются рисунками:
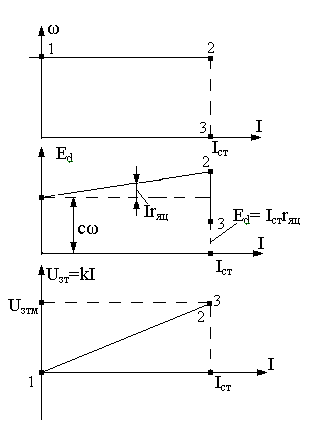
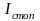 -
ток стопорения (максимальный ток);
-
ток стопорения (максимальный ток);
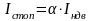 ;
;
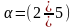 - кратность тока при кратковременной
перегрузке.
- кратность тока при кратковременной
перегрузке.
Т.к. регулятор
тока ПИ, то в установившемся режиме
должно выполняться равенство:
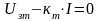 ;
;
Это условие
выполняется только тогда, когда РТ
работает в усилительном режиме (
или
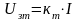 ).
).
Отсюда
следует, если оба регулятора работают
в усилительном режиме, то выходной
сигнал РС
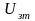 линейно растёт пропорционально току
нагрузки
.
В точке 2 РС переходит в режим насыщения.
При этом
линейно растёт пропорционально току
нагрузки
.
В точке 2 РС переходит в режим насыщения.
При этом
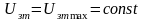 .
С учётом этого при дальнейшем приложении
нагрузки скорость начнёт падать по
прямой 2-3, а ток автоматически ограничивается
в соответствии с равенством, автоматически
уменьшается
.
С учётом этого при дальнейшем приложении
нагрузки скорость начнёт падать по
прямой 2-3, а ток автоматически ограничивается
в соответствии с равенством, автоматически
уменьшается
2. Сравнительный анализ статических характеристик в схемах с “пи” и “п” регуляторами скорости.
Изобразим входные цепи регуляторов скорости и тока.
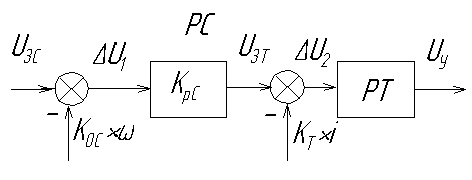
Для этого
узла схемы в установившемся режиме
справедливо равенство:
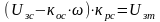 .
.
Решая это равенство относительно скорости, получаем уравнения электромеханической характеристики замкнутой системы.
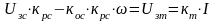 ;
;
т.к.
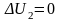 при “ПИ” регуляторе тока.
при “ПИ” регуляторе тока.
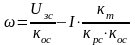 (1).
(1).
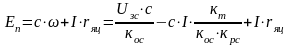 .
.
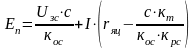 ;
(2)
;
(2)
В графическом виде (1) и (2) характеризуются рисунками
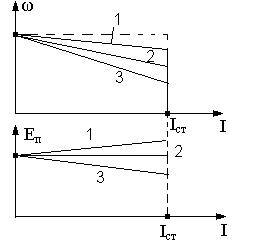
Анализируя
равенство (2) можно найти условие при
котором с ростом нагрузки
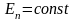
Если
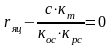 .
.
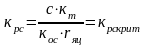 ;
(3)
;
(3)
При
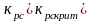 ,
тогда
,
тогда
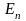 будет расти с ростом тока нагрузки. При
будет расти с ростом тока нагрузки. При
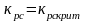 ,
жёсткость характеристики получается
как в разомкнутой схеме. При
,
жёсткость характеристики получается
как в разомкнутой схеме. При

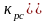 уменьшается с ростом тока нагрузки.
уменьшается с ростом тока нагрузки.
Если при
разности значений
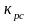 при заходе регулятора в насыщение
при заходе регулятора в насыщение
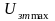 не меняется, то ток стопорения должен
оставаться одинаковым. Однако при
выполнении лабораторной работы важно
заметить, что в схеме с “П” – регулятором
с уменьшением
,
уменьшается и ток стопорения. Это
объясняется схемотехническими
особенностями самого регулятора в
режиме насыщения (уменьшается
).
не меняется, то ток стопорения должен
оставаться одинаковым. Однако при
выполнении лабораторной работы важно
заметить, что в схеме с “П” – регулятором
с уменьшением
,
уменьшается и ток стопорения. Это
объясняется схемотехническими
особенностями самого регулятора в
режиме насыщения (уменьшается
).
Из рассмотренного можно заключить, что качество статических характеристик принуждённо формируются регуляторами.
3. Структурная схема и особенности синтеза двухконтурной системы подчинённого регулирования с последовательной коррекцией. Особенности синтеза контура тока.
Синтез контура тока.
Из общей структурной схемы выделим контур тока.
Всю схему в этом контуре разобьём на две части: регулятор и объект. Под объектом понимаются все звенья, исключая РТ.
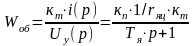 .
.
Если РТ типа “ПИ”, то следует задаться передаточной функцией разомкнутой сиcтемы типа “1”.
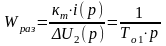 .
.
В общем виде передаточная функция регулятора тока (РТ):
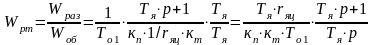
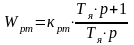 ;
;
Здесь введено обозначение
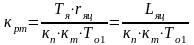 ;
;
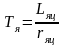 - электромагнитная постоянная времени
якорной цепи. По известным передаточной
функции разомкнутой системы, можно
записать передаточную функцию замкнутой
системы:
- электромагнитная постоянная времени
якорной цепи. По известным передаточной
функции разомкнутой системы, можно
записать передаточную функцию замкнутой
системы:
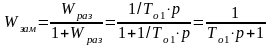 ;
;
4. Структурная схема и особенности синтеза контура скорости. Соответствие частотных характеристик и качества переходных процессов.
Зная передаточную функцию замкнутой системы контура тока, можно из общей структурной схемы выделить структурной схемы РЭП выделить структурную схему контура скорости, который имеет следующий вид.
Для замкнутой системы контура тока можно выделить передаточную функцию:
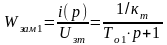 ;
;
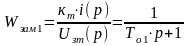 ;
;
Во втором
случае в качестве выходного сигнала
принимают сигнал обратной связи по току
(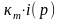 ).
Для контура скорости можно выделить
две передаточные функции:
).
Для контура скорости можно выделить
две передаточные функции:
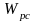 и
и
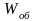 .
.
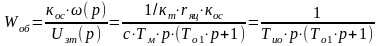 (1).
(1).
Здесь введено понятие постоянной интегрирования объекта:
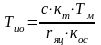 (2).
(2).
Чтобы систему сделать астатической нужно РС принять как ПИ регулятор и система становится типа 2-1-2
Если регулятор “ПИ”, то следует задаваться передаточной функцией разомкнутой системы типа “2 – 1 – 2”, который имеет следующий вид:
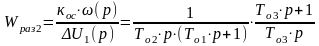 (3).
(3).
Отсюда можно найти передаточную функцию РС.
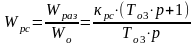 (4);
(4);
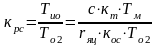 ;
;
По известной передаточной функцией разомкнутой системы, можно записать передаточную функцию замкнутой системы. Здесь также как для контура скорости, можно выделить передаточную функцию:
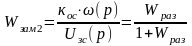
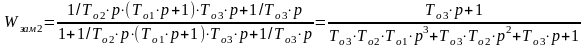
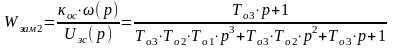 Удобно внести следующие обозначения:
Удобно внести следующие обозначения:
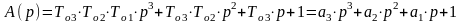
Здесь принимаем
скорость
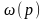 ,
а не сигнал обратной связи
,
а не сигнал обратной связи
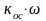 ;
;
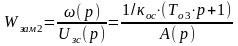 ;
;
Изобразим в качественном виде частотные характеристики этого контура.
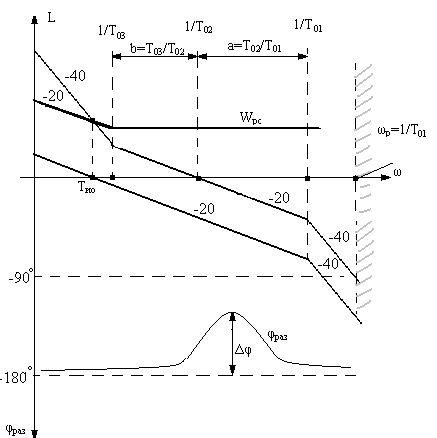
Для передаточной функции разомкнутой системы (3), можно записать выражение для фазочастотных характеристик различных систем. Здесь два интегрирующих звена:
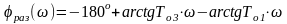 .Частотные
характеристики характеризуют динамические
характеристики системы в частотной
области.
.Частотные
характеристики характеризуют динамические
характеристики системы в частотной
области.
5. Анализ переходных процессов в системе типа «1-2», “2-1-2”.
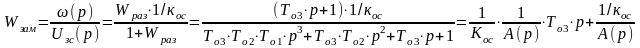
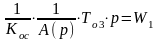
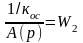
ω(t)=ω1(t)+ω2(t)
Равенство раскрывает сущность влияния форсирующего звена задание скорости. Если форсирующее звено отсутствует то отсуттвует и W1.
Если корни действительные отрицательные, то ПП монотонный без перерегулирования, если имеются комлексно сопряженные корни, то принимает колебательный характер
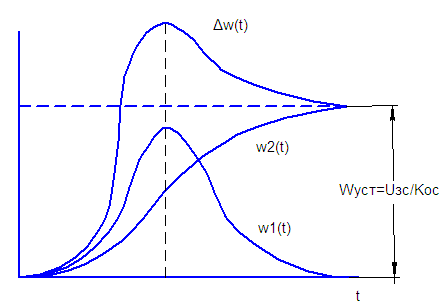
Если есть W1,есть и перерегулирование.
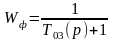 -фильтр
-фильтр
ω1-исчезает но ПП замедляется на номинальном участке.
а=3;b=3-биноминальная настройка σ=40%
а=2;b=2-по Батерворту σ=43% но если есть фильтр то σ=7% колебательность.
6. Двухзонный электропривод, назначение, статические характеристики.
П еред
пуском двигателя (
еред
пуском двигателя (
 )
происходит вначале процесс возбуждения
двигателя до номинального магнитного
потока. Уровень насыщения регулируемой
ЭДС
)
происходит вначале процесс возбуждения
двигателя до номинального магнитного
потока. Уровень насыщения регулируемой
ЭДС
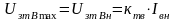 .
Как только скорость превысит граничную,
то регулируемая ЭДС заходит в усилительный
режим и его выходной сигнал
.
Как только скорость превысит граничную,
то регулируемая ЭДС заходит в усилительный
режим и его выходной сигнал
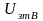 автоматически регулирует ток возбуждения
до заданного значения. Проведём
качественный анализ статических
характеристик для случая
автоматически регулирует ток возбуждения
до заданного значения. Проведём
качественный анализ статических
характеристик для случая
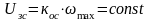 .
.
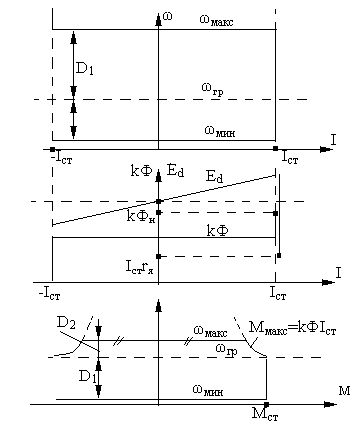 Связь
между магнитным потоком и скорости
двигателя во втором диапазоне регулирования
можно найти исходя из равенства:
Связь
между магнитным потоком и скорости
двигателя во втором диапазоне регулирования
можно найти исходя из равенства:
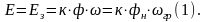
С дугой стороны
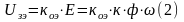 ,
,
отсюда
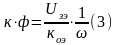 ,
где
,
где
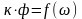 - это гиперболическая функция. Во втором
диапазоне регулирования на участке
ограниченного тока, когда
- это гиперболическая функция. Во втором
диапазоне регулирования на участке
ограниченного тока, когда
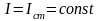 электромагнитный момент принимает
максимальное значение и описывается
равенством:
электромагнитный момент принимает
максимальное значение и описывается
равенством:
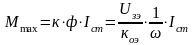 - гиперболическая функция.
- гиперболическая функция.
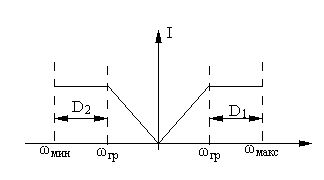
Если в установившемся режиме рассматривать поведение ЭДС двигателя в функции скорости, то эта зависимость характеризуется рисунком:
7. Переходный процесс при возбуждении двигателя в двухзонном РЭП.
Структурная схема имеет вид:
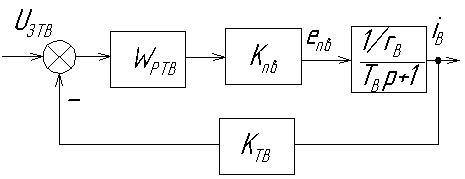
В двухзонных
ЭП, где переходные процессы влияют на
производительность механизмов,
возбудитель выбирают с форсировкой по
входному напряжению (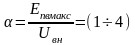 ;
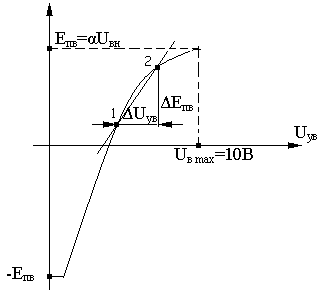
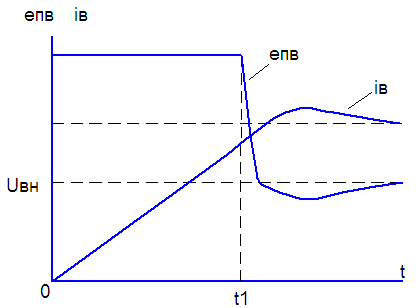
На характеристике вход - выход ТПВ
желательно указать две точки, при которых
поток номинальный и минимальный.
;
На характеристике вход - выход ТПВ
желательно указать две точки, при которых
поток номинальный и минимальный.
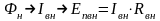 (точка1),
(точка1),
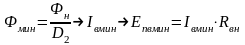 (точка 2).
(точка 2).
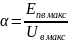
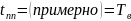
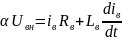
8. Анализ переходных процессов при наличии задатчика интенсивности на входе РЭП
С помощью задатчика интенсивности удается обеспечить заданные ускорения и замедления при разных нагрузках. Это важно при разных технологических процессах и в частности в транспортных механизмах.
РЭП с задатчиком интенсивности можно представить схемой:
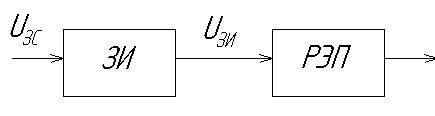
В большинстве случаев ЗИ формирует входной сигнал, линейно меняющийся во времени. Связь между входными и выходными сигналами ЗИ можно характеризовать временной диаграммой:
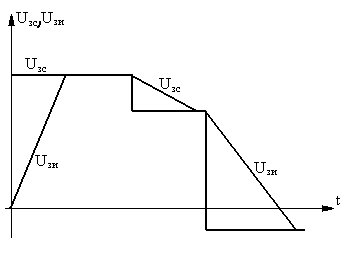
ЗИ – простейшее устройство, формирующее на входе РЭП линейно меняющийся сигнал. Обычно при анализе процессов не учитывают электромагнитные процессы в цепи якоря и механические процессы. С учетом этого можно записать следующее равенство:
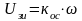 (1);
(1);
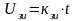 (2);
(2);
Тогда :
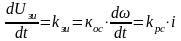 ,
,
где
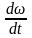 =ε;
=ε;
Отсюда устанавливается связь:
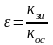 (3);
(3);
Отсюда ускорение не зависит от нагрузки.
Приведем анализ переходных процессов. Их удобно рассматривать как во временной области так и на фазовой плоскости в координатах: ω=f(I), ω=f(M).
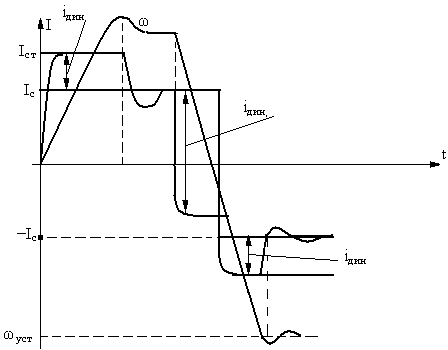
П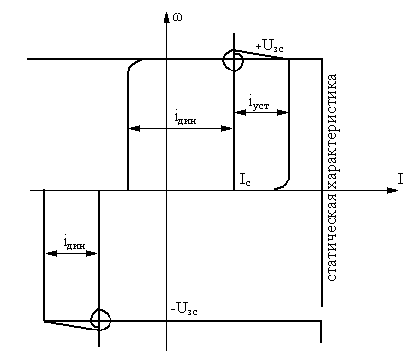 ереходные
процессы для тока и скорости принимают
следующий вид:
ереходные
процессы для тока и скорости принимают
следующий вид:
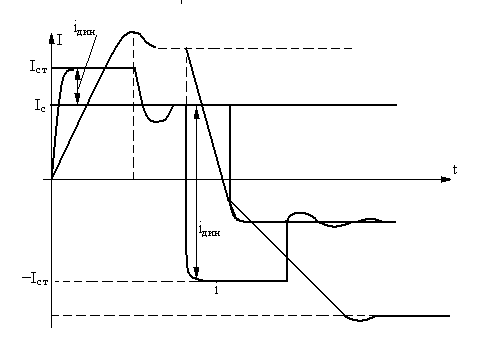
Для большей наглядности,сравнительный анализ с процессами когда зи отсутствует, а так в переходных процессах ограничивается при насыщении регулятора скорости. Этот случай характеризуется рисункам:
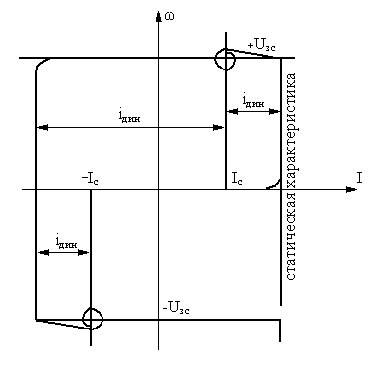 При
реактивной нагрузке в момент прохождения
скорости через нуль, момент и ток
статический меняется скачком, ускорение
в кривой скорости может возникнуть
излом.
При
реактивной нагрузке в момент прохождения
скорости через нуль, момент и ток
статический меняется скачком, ускорение
в кривой скорости может возникнуть
излом.
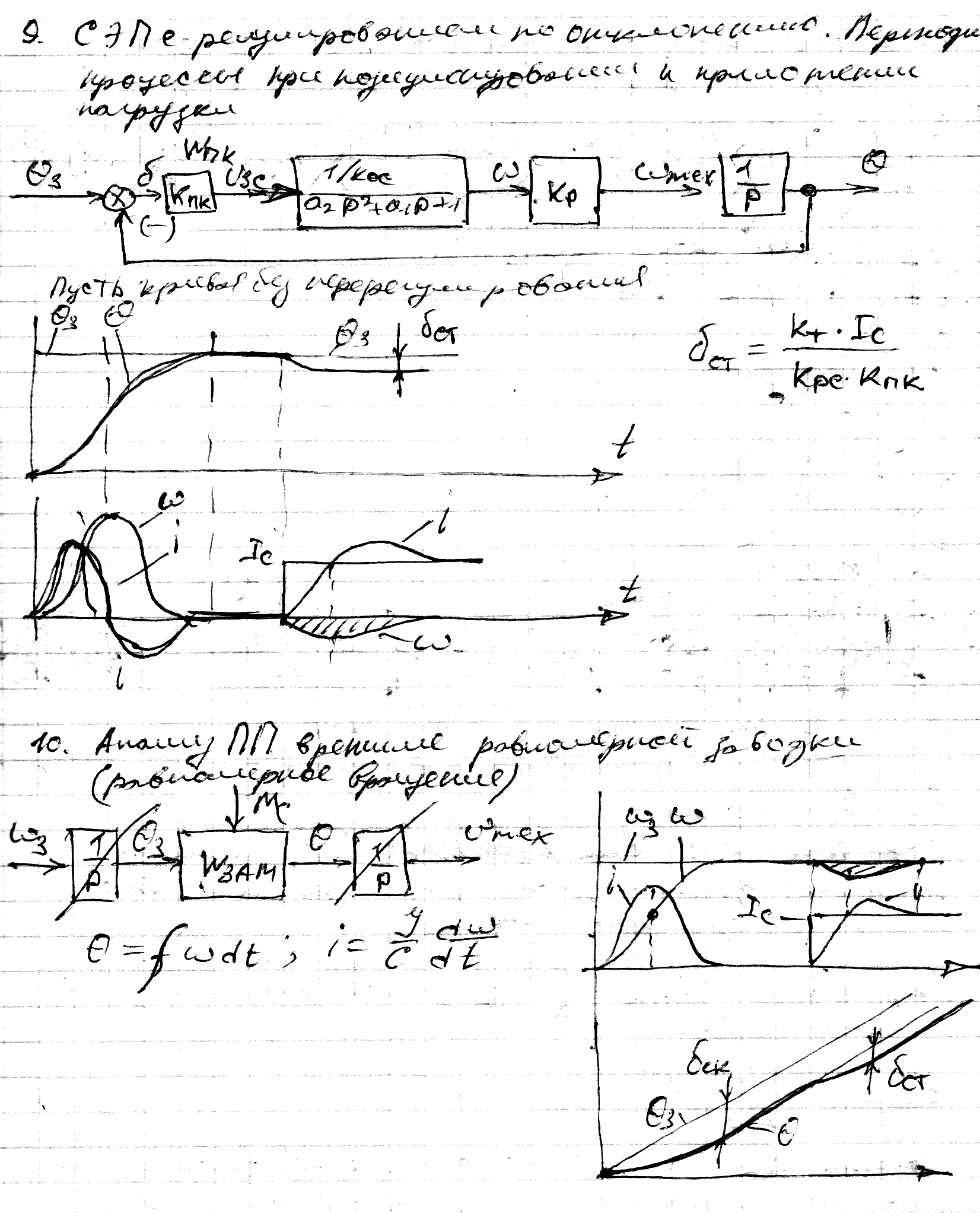
9. СЭП с регулированием по отклонению. Переходные процессы при позиционировании и приложении нагрузки.
10. СЭП в режиме работы с постоянной скоростью. Скоростная ошибка.
11. СЭП с комбинированным управлением. Свойства, анализ переходного процесса в режиме равномерного вращения
С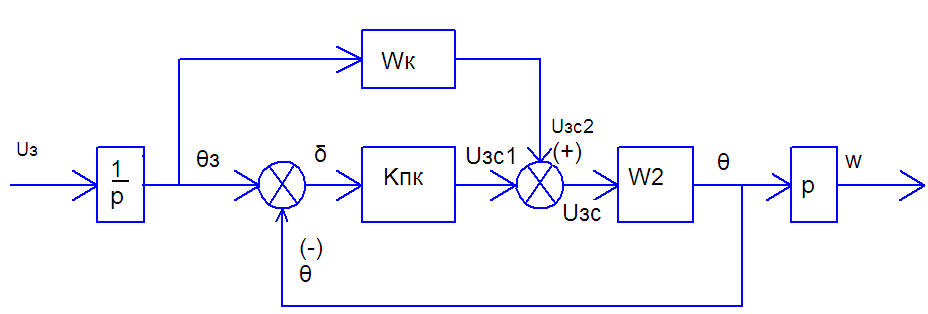 труктурная
схема имеет вид:
труктурная
схема имеет вид:
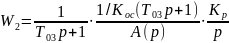 (1)
(1)
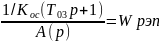
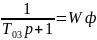
A(p)=a3p3+a2p2+a1p+1 (2)
Приведенный схеме (1) управление ведется по 2 каналам. По одному каналу из них задание скорости задается в формуле ошибки δ,а по формуле через звено передаточная функция Wк.
Wk*W2=1 или Wk=1/ W2 (3)
Это условие при которых полностью компенсируется влияние инерционности перед.функции W2/
Реализовать это условие можно теоретически
Из (3) находим:
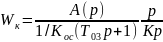 (4)
(4)
Воспользуемся самым простым случаем, получая формула (4) что в расмотренном режиме все производные равны 0,то есть р=0.
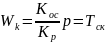 р
(5)
р
(5)
Это идеальное дифференцирующее звено, которое можно реализовать практически при наличие ДП конечной цепи.
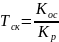 -постоянная
времени в полной скоростной компенсации
-постоянная
времени в полной скоростной компенсации
Из
фор. (1) можно записать:
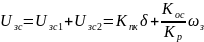
Т.к.
РС типа «ПИ»,то в установившемся режиме
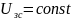 .
Тогда =>
.
Тогда =>
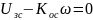
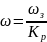 (6).-в установившемся режиме
(6).-в установившемся режиме
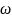 вала двигателя а следовательно и
механизма пропорциональна заданной
скорости
вала двигателя а следовательно и
механизма пропорциональна заданной
скорости
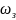 .Из
(6) следует что в установившемся режиме
скорость характеризует скорость движения
вала в установившемся режиме.
.Из
(6) следует что в установившемся режиме
скорость характеризует скорость движения
вала в установившемся режиме.
Из рассмотренного можно заключить, что введение в систему канала скоростной компенсации в установившемся режиме полностью исключается скоростная ошибка.
Скорость
в установившемся режиме задается
изменением
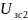 ,а
,а
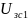 =0
или
=0
или
 .
.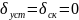
ПП в этом случае характеризуется рисунком
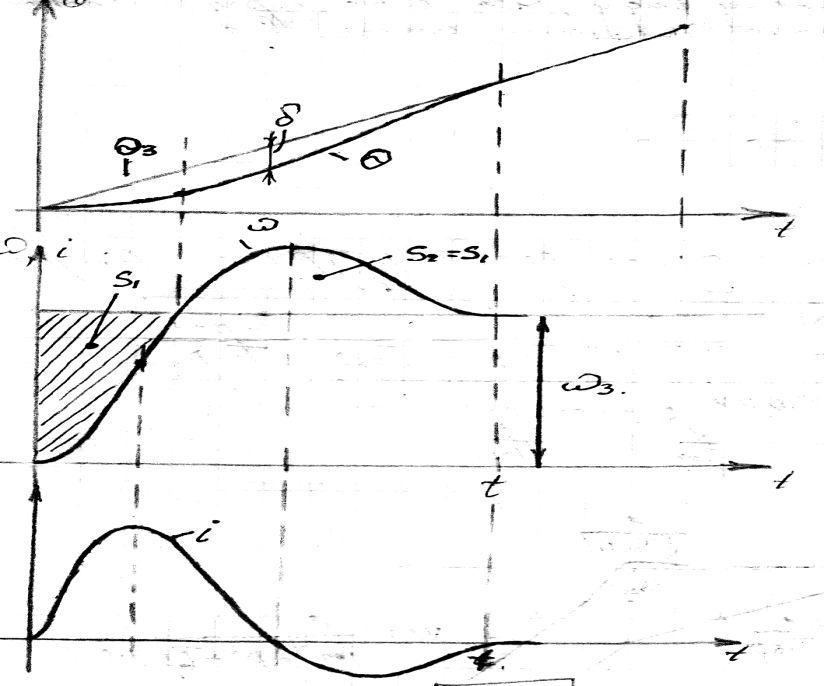
При приведенным кривым видно, что на начальном участке возникает динамическая ошибка, которая к моменту времени t стремится к нулю, машина переходит в режим идеального ХХ. На основном скорости находится в насыщении, а ток якоря ограничивается на заданном уровне.
Из кривых видно что канал скоростной компенсации устраняет скоростную ошибку и уменьшает динамическую ошибку, связанную с возмущением со стороны нагрузки.
