Плохотников К.Э. ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ. Теория и практика в среде MATLAB

Лекция №7 Поиск минимума Постановка задачи

Постановка задачи на поиск минимума выглядит следующим образом. Здесь и в дальнейшем будем искать минимум, при этом задача по поиску максимума легко может быть определена путем переформулировки задачи на минимум, заменой соответствующих неравенств на противоположные, inf на sup и соответственно min на max. Пусть имеется множество X, входящее в некоторое метрическое пространство. На множестве X определена скалярная функция F = F(x), xX. Говорят, что F(x) имеет локальный минимум в точке , если существует конечная  -окрестность этой точки, на которой выполняется

. (1)

Функция может иметь множество локальных минимумов, если же выполняется условие

, (2)

то говорят о достижении функцией абсолютного минимума на множестве X.

Необходимо наложить некоторые условия на множество X и вид функции F. Функция F должна быть хотя бы непрерывной (либо кусочно-непрерывной), т.к. иначе построить какой-либо разумный алгоритм поиска, кроме поиска минимума путем перебора, не остается. Если множество X — числовая ось, то задачи (1), (2) являются задачами поиска минимума функции одной вещественной переменной. Если X является n-мерным векторным пространством, то задачи (1), (2) являются задачами на минимум функции n переменных. Если X является некоторым функциональным пространством, то задача (1) является задачей минимизации соответствующего функционала.

Поиск абсолютного минимума состоит из нахождения всех локальных минимумов и выбора среди них минимального, т.е. задача (2) сводится к задаче (1). Поэтому в дальнейшем в основном будем заниматься решением задачи (1), т.е. поиском локальных минимумов.

Если множество X есть числовая ось, а функция F имеет непрерывную производную, то, как известно, решения задачи (1) являются корнями уравнения:

F(x) = 0. (3)

Если множество X есть n-мерное векторное пространство, то решения задачи (1) удовлетворяют системе уравнений вида:

. (3)

Для поиска минимума и вообще точек экстремума можно в принципе численно решить уравнения (3), (3). Однако в этом разделе будут рассмотрены прямые методы решения задачи (1).

Пусть множество X выделено в исходном пространстве с помощью некоторых условий типа равенств. В этом случае задачу (1) называют задачей на условный минимум (экстремум). Методом неопределенных множителей Лагранжа такие задачи можно свести к задаче на безусловный экстремум.

Задачу поиска минимума называют детерминированной, если погрешностью в определении функции F(x) можно пренебречь. Если погрешностью пренебречь нет возможности, задача называется стохастической. Здесь в основном рассматриваются детерминированные задачи.

Золотое сечение

Метод золотого сечения используется при поиске минимума функции одной вещественной переменной. Данный метод применим, в том числе и к недифференцируемым функциям.

Пусть на отрезке [a,b] задана кусочно-непрерывная функция F(x) и она имеет, включая концы отрезка [a,b], один-единственный локальный минимум. Построим итерационный процесс, сходящийся к искомому значению локального минимума.

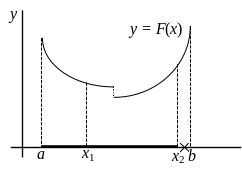
Рис.1. Иллюстрация к первому шагу итерационного процесса метода золотого сечения

Выберем внутри отрезка [a,b] две точки x₁ и x₂. Сравним значения функции F друг с другом в четырех точка: F(a), F(x₁), F(x₂), F(b). Пусть, например, значение функции в точке x₁ минимально, т.е. минимум находится на одном из отрезком, примыкающих к точке x₁, тогда третий отрезок, не примыкающий к x₁ может быть отброшен. Таким отрезком является отрезок [x₂,b]. На рис.1 приведена схема первого шага итерационного процесса в методе золотого сечения. Жирной линией выделена пара отрезков, на которых находится искомый минимум, крестом обозначен отрезок, подлежащий отбрасыванию.

На втором шаге итерационного процесса предыдущая процедура повторяется, но уже на отрезке [a,x₂]. Опять выбирается пара точек x₁, x₃ на отрезке [a,x₂], причем одна из них уже есть — это точка x₁. Вычисляются значения функции в этих точках, среди четырех значений F(a), F(x₁), F(x₃), F(x₂) находится минимум, отбрасывается отрезок, не примыкающий к точке с минимальным значением функции. Легко понять, что отбрасывается всегда один из двух крайних отрезков. Этот процесс можно продолжать неограниченно.

Определимся с выбором точек на соответствующих отрезках. При выборе точек будем следовать правилу золотого сечения. Пусть на отрезке [a,b] выбрана некоторая точка x_*, эта точка делит [a,b] на два отрезка: [a,x_*] и [x_*,b]. Возможны два варианта: первый отрезок меньше второго и второй меньше первого. Для первого варианта (аналогично для второго ) воспользуемся правилом золотого сечения: отношение длины большего отрезка ко всему отрезку [a,b] равно отношению длины меньшего отрезка к длине большего . Соответствующая пропорция для первого варианта имеет следующий вид:

. (4)

Из двух уравнений (4) можно найти уравнение для коэффициента :

. (5)

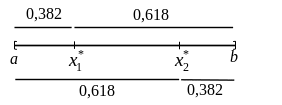
Рис.2. Два варианта золотого сечения отрезка

При решении квадратного уравнения в (5) выбран положительный корень уравнения. Для второго варианта расположения точки на отрезке [a,b] получится аналогичное уравнение для коэффициента . На рис.2 приведены оба варианта позиционирования точек и на отрезке [a,b] и соответствующие доли исходного отрезка, на которые делят точки исходный отрезок. Каждая из двух позиций точек и есть позиция золотого сечения отрезка. Из построения, а также согласно схеме рис.2, для точек и верно соотношение:

или . (6)

Согласно (6), зная одну из точек и , находим другую.

В соответствие со схемой рис.2 будем выбирать пару точек на отрезке, т.е. точки x₁ и x₂ на первом шаге итерационного процесса являются точками золотого сечения отрезка [a,b]. На втором шаге итерационного процесса точка x₁ уже делит отрезок [a,x₂] согласно второму варианту золотого сечения. Осталось найти позицию золотого сечения первого варианта для точки x₃. Этот процесс можно продолжать неограниченно.

После проведения очередного этапа итерационного процесса отрезок сокращается, т.к. отбрасывается меньшая часть (0,382я доля). Отрезок уменьшается в раза. После n шагов итерационного процесса длина отрезка составит  ⁿ долю длины первоначального отрезка. Таким образом, процесс при n   сходится, т.к. длина отрезка уменьшается со скоростью геометрической прогрессии с показателем   0,618, т.е. метод золотого сечения всегда сходиться, причем линейно.

Пусть на некотором шаге итерационного процесса анализируются четыре точки , из них две точки являются концами соответствующего отрезка. Найдем значения функции в этих точках и выберем среди них минимум. Пусть минимум реализуется в точке x_i, т.е.

. (7)

Отбросим ту точку, которая максимально удалена от точки x_i. Пусть такой точкой является точка x_l, т.е.

. (8)

Определим позиционирование друг относительно друга оставшихся точек. Пусть, например, верно следующее неравенство

. (9)

Согласно (6), можно определить вторую, после точки x_i, точку x_p золотого сечения отрезка [x_k,x_j] по формуле:

. (10)

Этапы алгоритма золотого сечения (7) — (10) полностью описывают произвольный шаг итерационного процесса. Искомый минимум находится, где-то на отрезке [x_k,x_j], поэтому итерации могут быть прекращены по достижении заданной точности , т.е.

.

Метод золотого сечения является аналогом метода деления отрезка пополам, но применительно к задаче отыскания минимума. Метод прост и экономичен и всегда сходится. Если на исходном отрезке несколько локальных минимумов, то процесс сойдется к одному из локальных минимумов не обязательно наименьшему.

На листинге_№1 приведен код программы поиска минимума функции методом золотого сечения. Для примера выбрана несколько экзотическая, кусочно-дифференцируемая функция, имеющая на заданном отрезке три локальных минимума. За счет незначительного изменения положения левой границы исходного отрезка удается последовательно получить методом золотого сечения все три локальных минимума функции.

Листинг_№1

%Программа поиска минимума функции методом

%золотого сечения

%очищаем рабочее пространство

clear all

%определяем размеры исходного отрезка [a,b]

a=0.95; b=3.5;

%определяем функцию, минимум которой на

%отрезке [a,b] находится

f=@(x)x^2*sign(x-1)*sign(x-1.5)*...

sign(x-2)*sign(x-2.5)*sign(x-3);

%определяем точность нахождения точки минимума

eps=1e-10;

%определяем константу ksi

ksi=(sqrt(5)-1)/2;

%определяем левую и правую границы отрезка

xl=a; xr=b;

%определяем номер итерации

k=0;

%организуем цикл метода поиска точки минимума

%методом золотого сечения

while xr-xl>eps

%определяем пару средних точек xl2 и xr2

%на отрезке [xl,xr] точек

xl2=xr-ksi*(xr-xl);

xr2=xl+ksi*(xr-xl);

%находим значения минимизируемой функции

%в четырех точках

Fl=f(xl); Fl2=f(xl2); Fr2=f(xr2); Fr=f(xr);

%перебор четырех вариантов минимума из

%четырех значений функции Fl, Fl2, Fr2, Fr

%минимально Fl

if (Fl<=Fl2)&(Fl<=Fr2)&(Fl<=Fr)

%отбрасывается точка xr

xl=xl; xr=xr2;

if xl2-xl>=xr-xl2

xr2=xl2; xl2=xl+xr-xr2;

else

xl2=xl2; xr2=xl+xr-xl2;

end

end

%минимально Fl2

if (Fl2<=Fr)&(Fl2<=Fr2)&(Fl2<=Fr)

%отбрасывается точка xr

xl=xl; xr=xr2;

if xl2-xr>xr-xl2

xr2=xl2; xl2=xl+xr-xr2;

else

xl2=xl2; xr2=xl+xr-xl2;

end;

end

%минимально Fr2

if (Fr2<=Fr)&(Fr2<=Fl2)&(Fr2<=Fr)

%отбрасываем точку xl

xl=xl2; xr=xr;

if xr2-xl2>=xr-xr2

xr2=xr2; xl2=xl+xr-xr2;

else

xl2=xr2; xr2=xl+xr-xl2;

end

end

%минимально Fr

if (Fr<=Fl)&(Fr<=Fl2)&(Fr<=Fr2)

%отбрасываем точку xr

xl=xl; xr=xr2;

if xl2-xl>=xr-xl2

xr2=xl2; xl2=xl+xr-xr2;

else

xl2=xl2; xr2=xl+xr-xl2;

end

end

k=k+1;

%запоминаем полусумму крайних точек отрезка

root(k)=0.5*(xr+xl);

end

%рисуем график зависимости значения точки

%минимума от номера итерации

plot(1:k,root);

На рис.3,а приведен график минимизируемой функции. Согласно графику функция имеет три локальных минимума x_min = 1, 2, 3. Метод золотого сечения обязательно сходится к одному из локальных минимумов. Графики на рис.3,б, 3,в и 3,г показывает сходимость к локальным минимумам в точках x_min = 1, 2, 3 при численных значениях левой границы исходного отрезка, равных a = 0,25; 0,5; 0,95 соответственно. Таким образом в методе золотого сечения, вычисление разных локальных минимумов (если они есть) возможно благодаря вариации одной или обеих границ исходного отрезка минимизации исследуемой функции.