1.2 Явища дифракції та інтерференції світла, зони Френеля

Дифракційні явища дуже широко поширені в природі. У сучасній фізиці існують такі терміни як: дифракція світлових хвиль, звукових і т.д. Елементарний приклад дифракції можна помітити у водному середовищі: якщо кинути камінь у воду то від місця його занурення будуть розповсюджуватися концентричні хвилі, якщо на шляху цих хвиль помістити дощечку з щілиною то ми можемо помітити явні ознаки дифракції хвиль. На цьому самому прикладі ми можемо переконатися в тому, що хвилі, проходячи через дощечку уже з двома отворами, посилюються. Ми бачимо, що зона впливу хвиль на екран значно збільшилася в порівняні з попереднім випадком. Такий самий ефект можна спостерігати, якщо пропускати світло через зонну пластинку Френеля. Зона пластинка Френеля – плоскопаралельна скляна пластинка з вигравійованими концентричними колами, радіус яких збігається з радіусами зон Френеля. Зонна пластинка «вимикає» парні або непарні зони Френеля, чим виключає взаємну інтерференцію (погашення) від сусідніх зон, що призводить до збільшення освітленості точки спостереження. Таким чином зонна пластинка діє як вбираюча лінза. Ми бачимо, що в зонній пластинці важливу роль грають концентричні кола такого самого радіусу як зони Френеля. Зони Френеля – ділянки, на які розбивають поверхню фронту світлової хвилі для спрощення обчислень, при визначенні амплітуди хвилі в заданій точці.

1.3 Розрахунок радіуса зон Френеля для світла

Нехай поверхню S представляє собою положення хвильового фронту в деякий момент. Для того щоб визначити коливання в деякій точці P, викликане хвилею, по Френелю потрібно спочатку визначити коливання, які викликаються в цій точці окремими вторинними хвилями, що приходять в неї від усіх елементів поверхні S (ΔS1, ΔS2 і т. д.), і потім скласти ці коливання з урахуванням їх амплітуд і фаз. При цьому слід враховувати тільки ті елементи хвильової поверхні S, які не загороджують які-небудь перешкоди.

Розглянемо як приклад просте дифракційне завдання про проходження плоскої монохроматичної хвилі від віддаленого джерела через невелике круглий отвір радіусу R в непрозорому екрані.

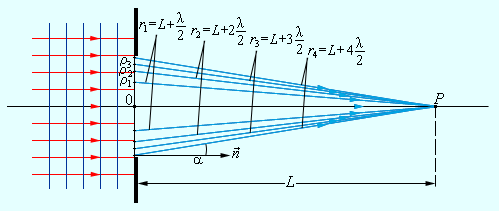
Рис 2.2.1 Дифракція плоскої хвилі на екрані з круглим отвором.

Точка спостереження P знаходиться на осі симетрії на відстані L від екрану. Відповідно до принципу Гюйгенса-Френеля слід подумки заселити хвильову поверхню, яка збігається з площиною отвору, вторинними джерелами, хвилі від яких сягають точки P. У результаті інтерференції вторинних хвиль у точці P виникає деякий результуюче коливання, квадрат амплітуди якого (інтенсивність) потрібно визначити при заданих значеннях довжини хвилі λ, амплітуди A0 падаючої хвилі і геометрії завдання. Для полегшення розрахунку Френель запропонував розбити хвильову поверхню падаючої хвилі в місці розташування перешкоди на кільцеві зони (зони Френеля) за наступним правилом: відстань від кордонів сусідніх зон до точки P повинні відрізняється на пів довжини хвилі, тобто

Якщо дивитися на хвильову поверхню з точки P, то межі зон Френеля будуть представляти собою концентричні кола (рис. 2.2.2).

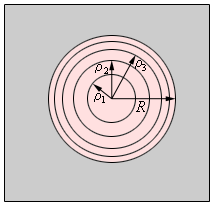
Рис. 2.2.2 Межі зон Френеля в площіні отворів

З рис. 2.2.1 легко знайти радіуси ρm зон Френеля:

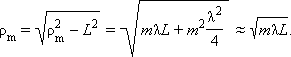
Так в оптиці λ <<L, другим членом під корінням можна знехтувати. Кількість зон Френеля, укладаються на отворі, визначається його радіусом R:

Тут m - не обов'язково ціле число. Результат інтерференції вторинних хвиль у точці P залежить від числа m відкритих зон Френеля. Легко показати, що всі зони мають однакову площу:

Однакові за площею зони повинні були б порушувати в точці спостереження коливання з однаковою амплітудою. Однак у кожної наступної зони кут α між променем, проведеним у точку спостереження, і нормаллю до хвильової поверхні зростає. Френель висловив припущення (підтверджене експериментом), що із збільшенням кута α амплітуда коливань зменшується, хоча і незначно:

A1> A2> A3> ... > A1,

де Am - амплітуда коливань, викликаних m-й зоною.

З гарним наближенням можна вважати, що амплітуда коливань, що викликаються деякої зоною, дорівнює середньому арифметичному з амплітуд коливань, що викликаються двома сусідніми зонами, тобто

Так як відстані від двох сусідніх зон до точки спостереження відрізняються на λ / 2, отже, порушених цими зонами коливання знаходиться в протифазі. Тому хвилі від будь-яких двох сусідніх зон майже гасять один одного. Сумарна амплітуда в точці спостереження є

A = A1 - A2 + A3 - A4 + ... = A1 - (A2 - A3) - (A4 - A5) - ... <A1.

Таким чином, сумарна амплітуда коливань у точці P завжди менше амплітуди коливань, які спричинила б одна перша зона Френеля. Зокрема, якщо б були відкриті всі зони Френеля, то до точки спостереження дійшла б хвиля з амплітудою A0. У цьому випадку можна записати:

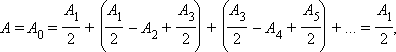
так як вираження, що стоять у дужках, дорівнюють нулю. Отже, дія (амплітуда), викликана всім хвильовим фронтом, дорівнює половині дії однієї першої зони.

Отже, якщо отвір у непрозорому екрані залишає відкритою тільки одну зону Френеля, то амплітуда коливань у точці спостереження зростає в 2 рази (а інтенсивність у 4 рази) в порівнянні з дією незбуреної хвилі. Якщо відкрити дві зони, то амплітуда коливань звертається в нуль. Якщо виготовити непрозорий екран, який залишав би відкритими тільки кілька непарних (або тільки кілька парних) зон, то амплітуда коливань різко зростає. Наприклад, якщо відкрито 1, 3 та 5 зони, то

A = 6A0, I = 36I0.

Такі платівки, що володіють властивістю фокусувати світло, називаються зонними пластинками.

При дифракції світла на круглому диску закритими виявляються зони Френеля перших номерів від 1 до m. Тоді амплітуда коливань у точці спостереження буде дорівнює

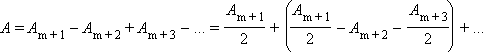
або A = Am + 1 / 2, так як вираження, що стоять у дужках, дорівнюють нулю. Якщо диск закриває зони не дуже великих номерів, то Am + 1 ≈ 2A0 і A ≈ A0, тобто в центрі картини при дифракції світла на диску спостерігається інтерференційний максимум. Це - так зване пляма Пуассона, воно оточене світлими і темними дифракційними кільцями.

Оцінимо розміри зон Френеля. Нехай, наприклад, дифракційна картина спостерігається на екрані, розташованому на відстані L = 1 м від перешкоди. Довжина хвилі світла λ = 600 нм (червоне світло). Тоді радіус першої зони Френеля є

Таким чином, в оптичному діапазоні внаслідок малості довжини хвилі розмір зон Френеля виявляється досить малим. Дифракційні явища проявляються найбільш виразно, коли на перешкоді укладається лише невелике число зон:

Це співвідношення можна розглядати як критерій спостереження дифракції. Якщо число зон Френеля, укладаються на перешкоді, стає дуже великим, дифракційні явища практично непомітні:

Ця нерівність визначає кордон застосовності геометричної оптики. Вузький пучок світла, який в геометричній оптиці називається променем, може бути сформований тільки при виконанні цієї умови. Таким чином, геометрична оптика є граничним випадком хвильової оптики.

Вище було розглянуто випадок дифракції світла від віддаленого джерела на перешкодах круглої форми. Якщо точкове джерело світла знаходиться на кінцевій відстані, то на перешкоду падає сферична хвиля. У цьому випадку геометрія завдання ускладнюється, тому що зони Френеля тепер потрібно будувати не на плоскій, а на сферичній поверхні.

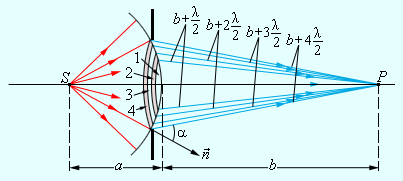
Рис. 2.2.3 Зони Френеля на сферичному фронті хвилі.

Розрахунок призводить до наступного виразу для радіусів ρm зон Френеля на сферичному фронті хвилі:

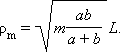
Усі висновки викладеної вище теорії Френеля залишаються справедливими і в цьому випадку.