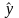Тема 5. Выборочное наблюдение

Задача 3.

Для изучения экономической активности населения района из 200 000 человек методом случайного бесповторного отбора опрошено 4 000 человек. Из них 1 600 человек вложили свои ваучеры в инвестиционные фонды или акции предприятий. С вероятностью 0,954 определить пределы населения всего района, в которых находиться доля экономически активного населения района.

Решение:

Число единиц генеральной совокупности N=200000;

Число единиц выборочной совокупности n=4000;

Число единиц, обладающих данным признаком, в выборочной совокупности m=1600; р=0,954.

Вычисляем долю единиц, обладающим нужным признаком:

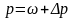, где

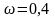
- предельная ошибка в выборке

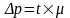, где - для бесповторной выборки.

При р=0,954 t=3

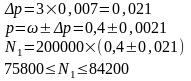
Ответ: пределы населения всего района N₁, в которых находиться доля экономически активного населения района, с вероятностью 0,954, от 75800 до 84200 человек.

Тема 6. Ряды динамики

Задача 3. имеется следующая информация:

дата	Размер имущества, тыс. рублей
На 01января	30
На 01 февраля	40
На 01 марта	50
На 01 апреля	30

Требуется: определить средний размер имущества предприятия за квартал.

Решение:

Средний уровень ряда

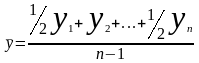
n=4

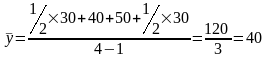тыс. рублей

Ответ: средний размер имущества за квартал 40 тыс. рублей.

Тема 7. Экономические индексы

Задача 3. Имеется информация о затратах на производство и индексах количества:

Вид продукции	Затраты на производство в I квартале, млн руб.	Изменение количества произведенной продукции во II квартале по сравнению с I кварталом, %
А Б В	20 12 15	+10 -13 +25

Требуется: определить: 1)индивидуальные индексы физического объема производства; 2) общий индекс физического объема производства; 3) общий индекс себестоимости, если известно, что общие затраты на производство выросли на 25%. Сделать выводы.

Решение:

Вид продукции А: количество произведенной продукции в отчетном периоде увеличилось на 10% по сравнению с базисным

Индивидуальный индекс физического объема по виду продукции А:

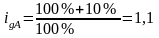
Аналогично по видам продукции Б и В

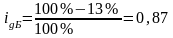
Общий индекс физического объема

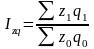
Сумма затрат в базисном периоде (общие затраты) равна 47 млн. руб. Из условий задачи известно, что общие затраты в текущем периоде увеличились на 25%, следовательно,

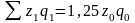
млн. руб.

Тема 8. Основы корреляционного анализа

Задача 3. На предприятии цены на изделия снижены с 80 руб. за единицу до 60 руб. После снижения цен продажа возросла с 400 до 500 единиц в день.

Требуется: Определить абсолютную и относительную эластичность. Сделать оценку эластичности с целью возможности (или невозможности) дальнейшего снижения цен.

Решение:

Абсолютная эластичность

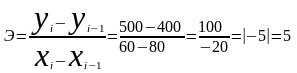
Относительная эластичность

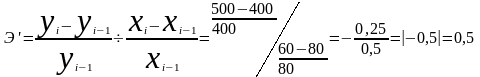
Абсолютная эластичность Э>1 (в нашем случае Э=5) показывает высокую эластичность, т.е. при снижении цены увеличивается объем продаж.

Эластичность относительная – это отношение между относительным изменением цены и обусловленным им относительным изменением объема сбыта. При Э<1 (в нашем случае Э=0,5) снижение цены ведет к росту количества проданных единиц товара, однако одновременно к снижению дохода (неэластичный спрос). Следовательно, дальнейшее снижение цен нецелесообразно. Дальнейшую зависимость определим корреляционным методом. Для проведения корреляционного анализа воспользуемся формулой (уравнение прямой). Необходимо найти значения а и b. Применим систему двух уравнений

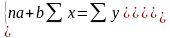
№ п/п	Цена х	Кол-во у		х2		Nx	Ny	Nx-Ny	(Nx-Ny)2
1	80	400	32000	6400	400	2	1	1	1
2	50	500	30000	3600	800	1	2	-1	1
	140	900	62000	10000					2

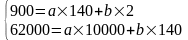
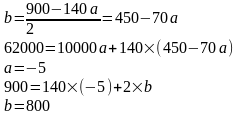
Для проверки правильности определенной зависимости вычисляем коэффициент Фехнера

, где

- сумма совпадений

- сумма несовпадений

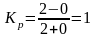, т.е зависимость прямая