2.4 Закон Амдала
Припустимо,
що алгоритм необхідної до вирішення
обчислювальної задачі, такий, в якого
частка
від загального об'єму обчислень може
бути отримана тільки послідовними
розрахунками, а, відповідно,
частка яка може бути розпаралелена
ідеально (тобто час обчислення буде
обернено пропорційно до числа задіяних
вузлів). Тоді прискорення, яке може бути
отримане на обчислювальній системі з
процесорів, в порівнянні з однопроцесорним
рішенням не перевищуватиме величини:
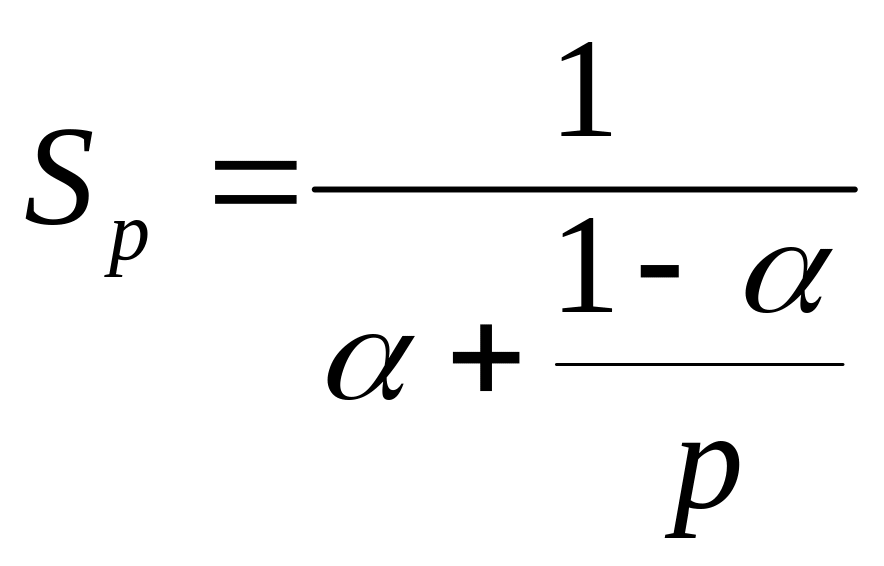(2.1)
Таблиця 2.1 показує, в скільки разів швидше виконається програма з часткою послідовних обчислень при використанні процесорів.
Таблиця 2.1 – Прискорення виконання програми з часткою послідовних обчислень при використанні процесорів
|
10 |
100 |
1000 |
0 |
10 |
100 |
1000 |
10% |
5.263 |
9.174 |
9.910 |
25% |
3.077 |
3.883 |
3.988 |
40% |
2.174 |
2.463 |
2.496 |
\
З
таблиці 2.1 видно, що тільки алгоритм, що
зовсім не містить послідовних обчислень
(
),
дозволяє отримати лінійний приріст
продуктивності із зростанням кількості
обчислювачів в системі. Якщо частка
послідовних обчислень в алгоритмі рівна
25 %, то збільшення числа процесорів до
10 дає прискорення в 3,077 разів, а збільшення
числа процесорів до 1000 дасть прискорення
в 3,988 разів.
Звідси
очевидно, що при частці послідовних
обчислень
загальний приріст продуктивності не
може перевищити
.
Так, якщо половина коду - послідовна, то
загальний приріст ніколи не перевищить
два.
Закон
Амдала показує, що приріст ефективності
обчислень залежить від алгоритму
завдання і обмежений зверху для будь-якого
завдання з
.
Не для всякого завдання має сенс
нарощування числа процесорів в
обчислювальній системі.
Більш того, якщо врахувати час, необхідний для передачі даних між вузлами обчислювальної системи, то залежність часу обчислень від числа вузлів матиме максимум. Це накладає обмеження на масштабованість обчислювальної системи, тобто означає, що з певного моменту додавання нових вузлів в систему збільшуватиме час розрахунку завдання.
Контрольні запитання
1 Чим відрізняються комп’ютерні системи класу SIМD від комп’ютерних систем класу SISD?
2 В чому відмінність мультипроцесорів від мультикомп’ютерів?
3 Комп’ютерні системи типу NOW чи СOW називаються кластерами?
4 Які типові топології схем комунікації процесорів в комп’ютерних системах з паралельною обробкою інформації?
5 Як класифікував комп’ютерні системи М.Флінн?
6 Які є рівні паралелізму?
Лекція №3 Конвеєрні комп’ютерні системи
3.1 Обробка інформації векторним процесором
У засобах векторної обробки під вектором розуміють одновимірний масив однотипних даних (зазвичай у формі з плаваючою комою), впорядкованих і певним чином розміщених в пам'яті КС. Якщо обробці піддаються багатовимірні масиви, їх також розглядають як вектори, адже при розміщенні матриці в пам'яті всі її елементи заносяться в комірки з послідовними адресами, причому дані можуть бути записані рядок за рядком або стовбець за стовбцем (рис.3.1).
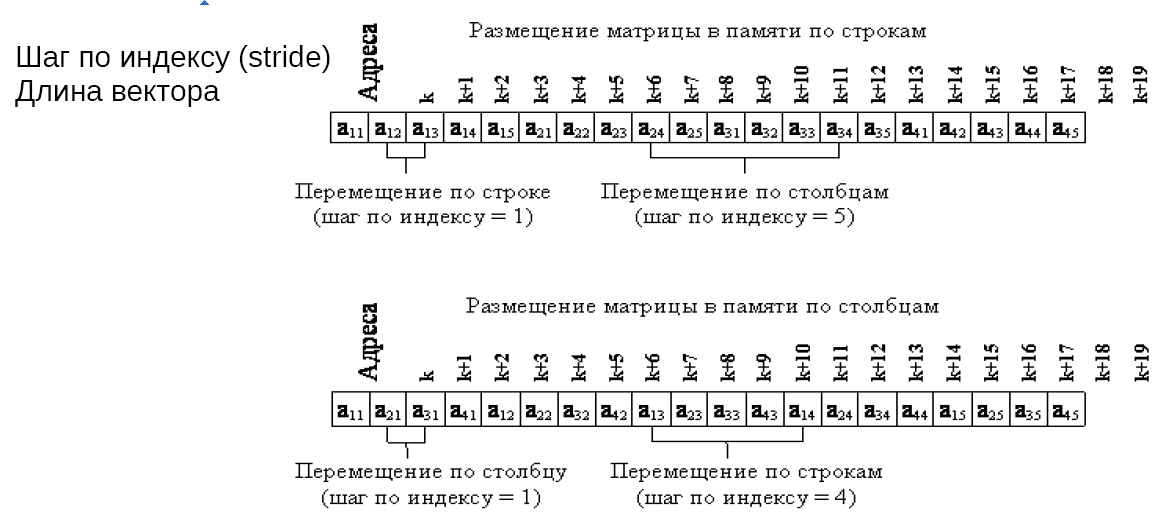
Рисунок 3.1 – Обробка векторним процесором багатовимірного масиву
Векторний процесор - це процесор, в якому операндами деяких команд можуть виступати впорядковані масиви даних - вектори.
Векторні комп'ютери маніпулюють масивами схожих даних подібно до того, як скалярні машини обробляють окремі елементи таких масивів. Це робиться за рахунок використання спеціально сконструйованих векторних центральних процесорів. При роботі у векторному режимі векторні процесори обробляють дані практично паралельно, що робить їх у декілька разів швидшими чим при роботі в скалярному режимі.
Розглянемо можливі підходи до архітектури засобів векторної обробки. Найбільш поширені з них зводяться до трьох груп:
- процесор з конвеєрним арифметико-логічним пристроєм;
- процесор з масивом паралельних арифметико-логічних пристроїв;
- масив паралельних процесорів.
Останній варіант є багатопроцесорною системою, відомою як матрична КС. Поняття векторного процесора має відношення до двох перших груп.
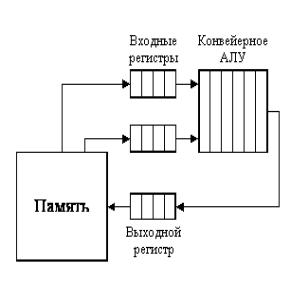
У варіанті з конвеєрним АЛП обробка елементів векторів проводиться конвеєрним АЛП для чисел з плаваючою комою. Операції з числами у формі з плаваючою комою достатньо складні, але піддаються розбиттю на окремі кроки. Наприклад, складання двох чисел зводиться до чотирьох етапів:
- порівняння порядків;
- зміщення мантиси меншого з чисел;
- складання мантис;
- нормалізації результату.
Кожен етап може бути реалізований за допомогою окремого ступеня конвеєрного АЛП. Черговий елемент вектора подається на вхід конвеєра, як тільки звільняється перший ступінь (рис.3.2).
П М С Н
|
|
Рисунок 3.2 – Процесор з конвеєрним арифметико-логічним пристроєм