6. Свойства пересечения и объединения множеств

. • ■ а

Из школьного курса математики известно, что операция, при помощи которой находят сумму чисел, называется сложе­нием. Над числами выполняют и другие операции, например умножение, вычитание, деление; при этом результат умноже­ния чисел называют произведением, деления - частным, т.е. для операций над числами и результатов этих операций суще­ствуют разные термины. Для рассмотренных операций над множествами ситуация иная: операции, при помощи которых находят пересечение и объединение множеств, называются соответственно пересечением и объединением.

Из школьного курса математики нам также известно, что операции над числами обладают рядом свойств. Например, сложение действительных чисел обладает переместительным и сочетательным свойствами: для любых действительных чисел а и Ъ справедливо равенство а + b = b + а, а для любых чисел a, b и с-равенство (а + Ь)+ с = а + ф + с).

Аналогичными свойствами обладает умножение действи­тельных чисел. Кроме того, для сложения и умножения выпол­няется распределительное свойство: для любых действительных чисел а, Ьис справедливо равенство: (a+b)c =ас + be.

Выясним, обладают ли «похожими» свойствами пересече­ние и объединение множеств.

Если обратиться к определениям пересечения и объедине­ния множеств, то можно увидеть, что в них не фиксируется порядок оперирования множествами. Например, выполняя объединение, можно к элементам одного множества присое­динить элементы другого, а можно поступить наоборот: к элементам второго множества присоединить элементы перво­го. (При этом надо только помнить, что в новом множестве не должно быть повторяющихся элементов.) Аналогичная си­туация и в случае, когда выполняется пересечение множеств. Это означает, что пересечение и объединение множеств обла­дают переместительным, или, как говорят в математике, ком- мутащ1тьш свойством: для любых множеств А и В выпол­няются равенства: Аг\В = Вг\АнА<иВ = ВиА.

Пересечение и объединение множеств обладают таюке со­четательным, или ассоциатшнш^ свойством: для любых множеств А, В и С выполняются равенства:

(АпВ)пС = Ап(ВпС) и (А и В) и С = А и (В и С)- Заметим, что назначение скобок в этих записях то же, что и в записях операций над числами.

Свойство ассоциативности для пересечения и объединения множеств не столь очевидно, как свойство коммутативности, и поэтому нуждается в доказательстве. Но прежде можно эти свойства проиллюстрировать при помощи кругов Эйлера. Рассмотрим, например, ассоциативное свойство пересечения множеств. Изобразим множества А, В и С в виде трех попарно пересекающихся кругов (рис. 9).

Рис.9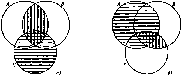

В выражении (А п В) п С скобки определяют следующий порядок действий: сначала выполняется пересечение множеств А и В -jOho показано на рисунке 9а вертикальной штрихов­кой, а затем находят пересечение полученного множества и множества С. Если выделить множество С горизонтальной штриховкой, то область, заштрихованная дважды, будет изо­бражать множество (А п В) п С.

Представим теперь наглядно множество А п (В о С). В соответствии с указанным порядком действий сначала надо найти пересечение множеств В и С - на рисунке 96 оно показано вертикальной штриховкой, а затем выполнить пересечение множества А с полученным множеством. Если отметить множество А горизонтальной штриховкой, то об­ласть, заштрихованная дважды, и будет изображать множе­ство А п (В п С).

Видим, что области, представляющие на рисунке 9 мно­жества (А п В) п С и А п (В п С), одинаковы, что и под­тверждает справедливость свойства ассоциативности для пересечения множеств.

Аналогично можно проиллюстрировать свойство ассоциа­тивности и для объединения множеств.

В чем важность ассоциативного свойства пересечения и объединения множеств? Во-первых, можно находить пересе­чение и объединение трех множеств, зная, как это делать для двух. Во-вторых, на основании этого свойства в выражениях А п (В п С), (А п В) п С, А и (В и С), (А и В) и С можно опускать скобки и писать А п В о С или А и В и С," что об­легчает запись.

Рассмотрим строгое доказательство свойства ассоциатив­ности одной из операций над множествами, например объе­динения, т.е. докажем, что для любых множеста ^ в^дливо равенство (А и В) и С = А и (В и С).

Чтобы доказать равенство двух множеств, надо убедиться в том, что каждый элемент множества (А и В) и С содержится в множестве А и (В и С), и наоборот.

1. Пусть х - любой элемент множества (А и В) и С. Тогда, по определению объединения, хе Ли В или хё С.

Если xjzj^u^B, то, по определению объединения, х е А или х е_В. В том случае, когда х е А, то, также по определе­нию объединения, х е А и (В у Су

Если хе В, то имеем, что хе ВиС^а значит, х е А и {В и С) . Случай, когда х е Акх е В, сводится к рассмотренным. Таким образом, из того, что хе Аи В, следует, что хе А и (В и С).

Если х е С, то, по определению объединения, х е В и С, и следовательно,хе AuJ&UjQ^

Случай, когда х е А и В и х е С, сводится к рассмотрен­ным выше. ~

Итак, мы показали, что каждый элемент множества (А и В) и С содержится и в множестве А и (В и С), т.е. (Ли В) и С с А и (В и С).

2. Пусть у - любой элемент множества А и (В и С). Тогда, по определению объединения, j; е А или у е В и С.

Если у е А, то, по определению объединения, у е А и В и, следовательно, у g Akj (Bkj С).

Если уеВиС,тоуеВ или j/g С.В том случае, когда у е В, то у е А и В и, значит, у е (А и В) и С. Когда же у е С, то у е (Akj B)\j С. Случай, когда у ё В и у е С, сводится к уже рассмотренным.

Итак, мы показали, что каждый элемент множества А и (В и С) содержится в мноЭкесЬгве (А и 5) и С, т.е.

Согласно определению равных множеств заключаем, что (Л и 5) и С = А и (Б и С), что и требовалось доказать.

Аналогично доказывается и ассоциативное свойство пере­сечения множеств.

Взаимосвязь пересечения и объединения множеств отража­ется в распределительных, или дистрибутивных, свойствах этих операций. Таких свойств два:

1. Пересечение дистрибутивно относительно объединения множеств, т.е. для любых множеств А, В и С выполняется равенство

(А и В) п С = (А п С) и (В п Q.

2. Объединение дистрибутивно относительно пересечения множеств, т.е. для любых множеств А, В и С выполняется равенство

(А п В) и С = (А и С) п (В и Q.

Заметим, что если в выражении есть знаки пересечения и объединения множеств и нет скобок, то сначала выполняют пересечение, так как считают, что пересечение более «силь­ная» операция, чем объединение. В связи со сказанным за­пись дистрибутивного свойства пересечения относительно объединения можно упростить, опустив скобки в правой части равенства.

Убедиться в справедливости сформулированных свойств можно путем доказательства, которое аналогично доказатель­ству свойства ассоциативности объединения.

Проиллюстрировать свойства дистрибутивности можно, используя круги Эйлера.

Если провести аналогию с действиями над числами, то можно увидеть, что дистрибутивное свойство пересечения относительно объединения сопоставимо с распределитель­ным свойством умножения относительно сложения при ус­ловии, что в качестве операции, аналогичной пересечению, рассматривать умножение, а для объединения - сложение.

Но для дистрибутивного свойства объединения множеств относительно пересечения аналогичного свойства над чис­лами нет.

Действительно, наличие такого свойства означало бы, что для всех чисел выполняется равенство a b + с = (а + с) (Ь + с), что невозможно. Подмеченное отличие говорит о том, что на­ряду с тем, что пересечение и объединение множеств обладают рядом свойств, аналогичных свойствам сложения и умножения чисел, операции над множествами обладают свойствами, кото­рых нет у операций над числами.

Завершая рассмотрение свойств пересечения и объедине­ния множеств, отметим еще следующее.

Понятие пересечения и объединения множеств можно обобщить на любое конечное число множеств:

А₇пА₂п ... пА„ = {х | х е А₇ихе А₂ и ... ихе А_п},

Aj kjA₂u ... иА„ = {х | х е Aj или хе А₂ или ... илих е А„}.

Аналогично можно поступить и по отношению к рассмот­ренным свойствам данных операций. ⁰

Упражнения

1. Известно, что х е А п В. Следует ли из этого, что

а)хеВпА; б)хеАиВ; в)хе ВиА?

2. Определите порядок выполнения действий в следующих выражениях:

а)АиВиС; в)АпВи СnD;

б)АпВп С; г) А и В п С и D.

3. Постройте три круга, представляющие попарно пересе­кающиеся множества А, В и С, и отметьте штриховкой облас­ти, изображающие множества:

а)АпВп С; в) (An В) и С; д) А и В п С;

б) А и В и С; г) (AvB)c\ С; е) (А и C)n(Bv Q.

Для каждого случая сделайте отдельный рисунок.

4. Проиллюстрируйте, используя круги Эйлера, следующие свойства:

а) ассоциативности пересечения множеств;

б) дистрибутивности пересечения относительно объедине­ния множеств;

в) дистрибутивности объединения относительно пересече­ния множеств.

5. Среди следующих выражений найдите такие, которые представляют собой равные множества:

ъ)РпМпК\ в)РпМиРпК; д)Ри(МпК);

б) Рп (Ми К); г) (РпМ)п К- е) (МиР)п (Р и К).

6. Даны множества: А - натуральных чисел, кратных 2; В - натуральных чисел, кратных 3; С - натуральных чисел, кратных 5.

а) Изобразите при помощи кругов Эйлера данные множе­ства и отметьте штриховкой область, изображающую множе­ство Л пВиС.

б) Сформулируйте характеристическое свойство элемен­тов этого множества и назовите 3 элемента, которые ему принадлежат.

в) Верно ли, что А и В п С = (А и В) п (А и С)?

7. Даны множества: Х- двузначных чисел, Y- четных на­туральных чисел, Р - натуральных чисел, кратных 4.

а) Укажите характеристическое свойство элементов каждо­го из множеств АиВ, если А = Хп Yn Р,В = Хг\ (7п Р).

б) Изобразите множества X, Y и Р при помощи кругов Эй­лера и покажите области, представляющие множества АиВ (для каждого случая выполните отдельный рисунок).

в) Верно ли, что 24 е А, а 23 е В1

8. А - множество треугольников, В - множество ромбов, С- множество многоугольников, имеющих угол 60° . Ука­жите характеристическое свойство элементов множества Х=АпСиВпСи начертите две фигуры, принадлежащие множеству X.

9. Докажите, что для любого множества А верны равенства:

а)Ап0 = 0; в) А п А = А;

б )Au0 = A; r)AuA=A.

10. Верно ли, что если А с В, то

а) А п В = А; 6)АиВ = В?