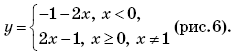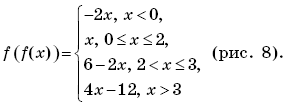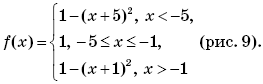Ответы:

1. 4,5. 2. 9. 3. [8,5; 13) c (13; +∞).

4.

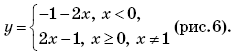
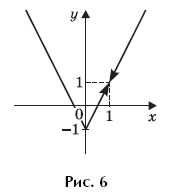
5.

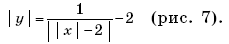
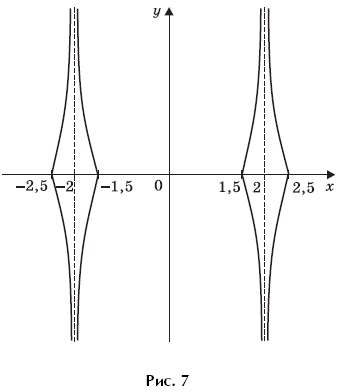
6.

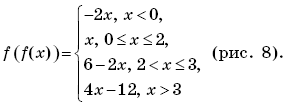
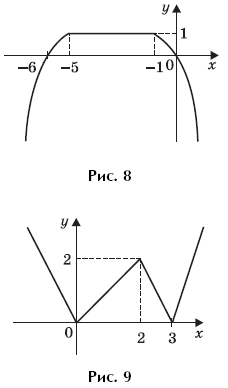
7.

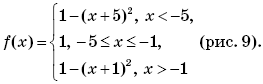
8. а) f(x) = x² – 5x + 6;

б) f(x) = x² – 14;

в) f(x) = x² – 2, x ≠ 0;

г) f(x) = 12 – x²;

д)

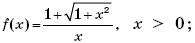
е)

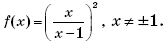
10. 0,8. 11. 2. 12. f(x) = 2.

13. 133. 14. Существует (и единственная!)

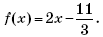
15. 2001². Указание. Достаточно доказать, что функция f(x) удовлетворяет функциональному уравнению f(x + a) = f(x – a) + 4ax при любом натуральном a. Это можно сделать, например, с помощью метода математической индукции. Тогда, положив x = a, из уравнения f(2a) = f(0) + 4a² можно вычислить f(2000): f(2000) = = 20002. Тогда получим f(2000 + 1) = f(2000) + + 2∙2000 + 1, или f(2001) = 20012. Замечание. Можно также доказать, что общее решение исходного функционального уравнения имеет вид f(x) = x² + g(x), где g(x) — произвольная периодическая функция с периодом T = 1, определенная на всей числовой прямой.

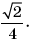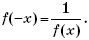16. Указание. Установите вначале, что f(0) = 1. Затем, показав, что f(x) ≠ 0, докажите равенство Выведите для всех натуральных n соотношение f(nx) = nⁿ(x). Поскольку f(4) = f(8∙0,5) или 16 = f⁸(0,5), то

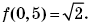
(Подумайте, почему f(x) > 0.) Тогда f(1,5) = f(3∙0,5). Замечание. Можно также доказать, что f(x) = 2^x для рациональных x.

17.

В. Бардушин ;

А. Белов ;

А. Прокофьев ;

Т. Фадеичева