5. Порядок выполнения работы:

   1. Запустить среду разработки .

   2. Выполнить следующее задание:

Задание

Составить имитационную модель и рассчитать показатели эффективности системы массового обслуживания (СМО) со следующими характеристиками:

- число каналов обслуживания n;

- максимальная длина очереди l;

- поток поступающих в систему заявок простейший со средней интенсивностью r и показательным законом распределения времени между поступлением заявок;

- поток обслуживаемых в системе заявок простейший со средней интенсивностью µ и показательным законом распределения времени обслуживания.

Сравнить найденные значения показателей с результатами, полученными путем численного решения уравнения Колмогорова для вероятностей состояний системы.

3. Сдать отчет по работе.

6. Содержание отчета:

   1. Наименование работы.

   2. Цель работы.

   3. Описание математической модели СМО.

   4. Описание реализации модели в среде MathLab.

7. Контрольные вопросы:

   1. Что называется системой массового обслуживания?

   2. Приведите примеры использования СМО на предприятиях отрасли связи?

   3. В чем суть компьютерного имитационного моделирования СМО?

   4. Какие возможности среды MathLab используются при разработке имитационных моделей СМО?

Лабораторная работа № 7

Статистическая обработка экспериментальных данных

1. Цель работы:

   1. Изучить возможности использования программного обеспечения для статистической обработки экспериментальных данных.

   2. Провести статистическую обработку данных с помощью надстройки «Пакет анализа» Microsoft Excel.

2. Литература:

   1. Чернышов Ю. Н. Информационные технологии в экономике и управлении : учеб. пособие для вузов / Ю. Н. Чернышов .- 2-е изд., испр. и доп.- М. : Горячая линия - Телеком, 2008

   2. Рагулина М. И. Информационные технологии в математике : учеб. пособие для студ. вузов / Рагулина М. И.; под ред. М. П. Лапчика .- М. : Академия, 2008.

   3. Сырецкий Г.А. Информатика. Фундаментальный курс. Том 1, 2. – Москва, 2005- 234с.

   4. Интернет-технологии в экономике знаний : учебник / под ред. Н. М. Абдикеева .- М. : ИНФРА-М, 2010

3. Основное оборудование:

   1. ПЭВМ.

   2. Электронные таблицы Microsoft Excel.

   3. Среда математической обработки данных MathCad.

4. Задание:

   1. Изучить теоретический материал по теме «Статистическая обработка экспериментальных данных».

   2. Решить задачи в электронных таблицах Excel и в среде MathCad.

   3. Составить отчет по работе.

5. Порядок выполнения работы:

   1. Выполнить задания.

   2. Сдать отчет по работе.

Задание 1.

По предприятию получены данные о расстоянии перевозки грузов в междугородном сообщении (км). Данные приведены в таблице 4.1.

Для анализа работы предприятия необходимо:

1) построить интервальный ряд распределения, определив величину интервала и количество интервалов по формуле Стерджеса;

2) дать графическое изображение ряда;

3) вычислить среднее значение, моду, медиану и стандартное отклонение.

Сформулировать вывод.

Таблица. Перевозка грузов в междугородном сообщении (км)

560	1060	420	1410	1500	400	3800	700	1780	450
449	285	1850	2200	800	1200	1540	1150	180	452
452	2500	300	400	900	1800	452	1850	1225	220
1800	300	920	1400	1400	480	850	200	400	1440
420	1700	1615	3500	300	320	600	965	450	245

Задание 2.

Фирма рассматривает вопрос о приобретении участка для нового магазина розничной торговли. Очень важным критерием при принятии этого решения является место положения магазина (насколько многолюдно). Чтобы выяснить это, представитель фирмы в течение 2 недель подсчитывает, сколько пешеходов проходит мимо участка. Результаты наблюдений составляют выборку из генеральной совокупности всех возможных дней. Данные наблюдений приведены в таблице.

Таблица. Количество прохожих.

544	468	399	759	526	212	256
456	553	259	469	366	197	178

Рассчитайте:

Среднее значение количества пешеходов. (Насколько точно оно отражает количество людей, которые будут проходить мимо магазина в любой конкретный день?)

Верхнюю и нижнюю границы доверительного интервала при уровне надежности 95%.

Теоретические сведения

Статистическая обработка данных и надстройка«Пакет анализа».

Целью статистического исследования является обнаружение и исследование соотношений между статистическими (экономическими) данными и их использование для изучения, прогнозирования и принятия решений.

Любые экономические данные представляют собой количественные характеристики каких-либо экономических объектов. Они формируются под действием множества факторов, не все из которых доступны внешнему контролю. Неконтролируемые факторы могут принимать случайные значения из некоторого множества значений и тем самым обусловливать случайность данных, которые они определяют. Стохастическая природа экономических данных обусловливает необходимость применения специальных статистических методов для их анализа и обработки.

В Excel реализованы функции, реализующие статистические методы обработки и анализа данных, и специальное программное расширение – надстройка «Пакет анализа». Эта надстройка входит в поставку Excel и может устанавливаться или не устанавливаться по желанию пользователя.

Для установки надстройки «Пакет анализа» надо выполнить следующие действия:

1. Выполнить команду «Сервис/ Надстройки».

2. В диалоговом окне «Надстройки» отметить пункт «Пакет анализа».

3. Нажать кнопку ОК.

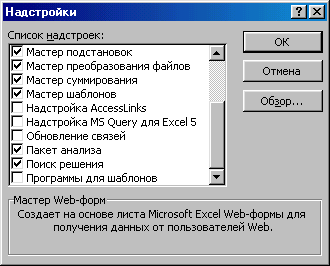
Рис. Установка пакета анализа.

Если установка завершается успешно, то в меню «Сервис» появляется пункт «Анализ данных». С помощью команд, доступных в окне «Анализ данных» (рис. 1.2), можно провести:

- описательный статистический анализ (Описательная статистика);

- ранжирование данных (Ранг и персентиль);

- графический анализ данных (Гистограмма);

- прогнозирование данных (Скользящее среднее, Экспоненциальное сглаживание);

- регрессионный анализ (Регрессия) и т.д.

Основные функции статистической обработки данных

Ниже описаны некоторые функции статистической обработки данных. Поскольку фундаментальными понятиями статистического анализа являются понятия вероятности и случайной величины, в ряде функций они используются в качестве аргументов. Большая часть таких функций представлена в приложении.

Таблица Функции статистической обработки данных.

Функция	Назначение функции и ее аргументы
ВЕРОЯТНОСТЬ	Возвращает вероятность того, что значение из интервала находится внутри заданных пределов. ВЕРОЯТНОСТЬ(x_интервал; интервал_вероятностей; нижний_предел; верхний_предел) X_интервал - это интервал числовых значений x, с которыми связаны вероятности. Интервал_вероятностей - это множество вероятностей, соответствующих значениям в аргументе x_интервал. Нижний_предел - это нижняя граница значения, для которого вычисляется вероятность. Верхний_предел - это необязательная верхняя граница значения, для которого требуется вычислить вероятность.
МАКС	Возвращает максимальное значение из списка аргументов. МАКС(число1; число2; ...) Число1, число2, ... - это от 1 до 30 чисел, среди которых ищется максимальное значение.
МЕДИАНА	Возвращает медиану заданных чисел. МЕДИАНА(число1; число2; ...) Число1, число2, ... - это от 1 до 30 чисел, для которых определяется медиана.
МИН	Возвращает минимальное значение из списка аргументов. МИН(число1; число2; ...) Число1, число2, ... - это от 1 до 30 чисел, среди которых ищется минимальное значение.
СРЗНАЧ	Возвращает среднее (арифметическое) своих аргументов. СРЗНАЧ(число1; число2; ...) Число1, число2, ... - это от 1 до 30 аргументов, для которых вычисляется среднее.
СТАНДОТКЛОН	Оценивает стандартное отклонение по выборке. СТАНДОТКЛОН(число1; число2; ...) Число1, число2, ... - это от 1 до 30 числовых аргументов, соответствующих выборке из генеральной совокупности. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.
СЧЁТ	Подсчитывает количество чисел в списке аргументов. Используется для получения количества числовых ячеек в интервалах или массивах ячеек. СЧЁТ(значение1; значение2; ...) Значение1, значение2, ... - это от 1 до 30 аргументов, которые могут содержать или ссылаться на данные различных типов, но в подсчете участвуют только числа.
ЧАСТОТА	Вычисляет частоту появления значений в интервале значений и возвращает массив цифр. ЧАСТОТА(массив_данных; массив_карманов) Массив_данных - это массив или ссылка на множество данных, для которых вычисляются частоты. Массив_карманов - это массив или ссылка на множество интервалов, в которые группируются значения аргумента массив_данных. Если массив_карманов не содержит значений, то функция ЧАСТОТА возвращает количество элементов в аргументе массив_данных.

Рассмотрим пример решения задачи с использованием статистических функций.

Данные о часовой интенсивности движения автомобилей на автомагистрали приведены в таблице

Таблица. Интенсивность движения автомобилей (авт/ч).

140	99	80	140	218	340	92	152	120	130
50	110	130	96	48	36	60	30	86	102
90	210	220	261	282	312	68	80	131	190

Для анализа загруженности магистрали:

1. вычислить среднее значение, моду, медиану и стандартное отклонение;

2. построить интервальный ряд распределения;

3. дать графическое изображение ряда.

Решение:

Вариант решения задачи приведен на рисунке 1.3.

1. В ячейки A2:J4 ввести исходные данные о загруженности автомагистрали.

2. Используя встроенные функции статистической обработки данных вычислить:

- в ячейке D6 среднее значение по формуле =СРЗНАЧ(A2:J4);

- в ячейке D7 моду по формуле =МОДА(A2:J4);

- в ячейке D8 медиану по формуле =МЕДИАНА(A2:J4);

- в ячейке D9 стандартное отклонение по формуле =СТАНДОТКЛОН(A2:J4).

3. Для построения интервального ряда необходимо определить число групп и величину интервала.

- Число групп приближенно определяется по формуле Стреджесса:

m=1+3,322*lg n,

где m - число групп (m - всегда целое, округляется в большую сторону),

n - общее число единиц совокупности.

- число групп рассчитываем в ячейке D13 по формуле =ОКРУГЛВВЕРХ(1+3,322*LOG10(СЧЁТ(A2:J4));0). Эта формула представляет запись в Excel формулы Стерджесса.

- величина интервала определяется по формуле:

i = R/m,

где R - размах признака (R= xmax-xmin).

- в ячейке D11 находим минимальное значение диапазона по формуле =МИН(A2:J4).

- в ячейке D12 находим максимальное значение диапазона по формуле =МАКС(A2:J4).

- в ячейке D14 находим величину интервала по формуле =ОКРУГЛВВЕРХ((D12-D11)/D13;0).

- в ячейках А17:А23 задать значения интервалов.

- в ячейке А17 задать нижнюю границу диапазона по формуле =ОКРУГЛВНИЗ(D11;0),

- в ячейку А18 ввести формулу =А17+$D$14,

- скопировать формулу из ячейки А18 в ячейки А19:А23.

- в ячейках В17:В23 определить частоты значений, попадающих в заданные диапазоны по формуле {=ЧАСТОТА(A2:J4;A17:A23)}.

Обратите внимание, что это формула возвращает блок, поэтому работу с мастером функций надо завершать нажатием комбинации клавиш Ctrl+Shift+Enter.

4. Для полученных данных построить гистограмму интервального ряда распределения.

Пример решения задачи приведен на рисунке.

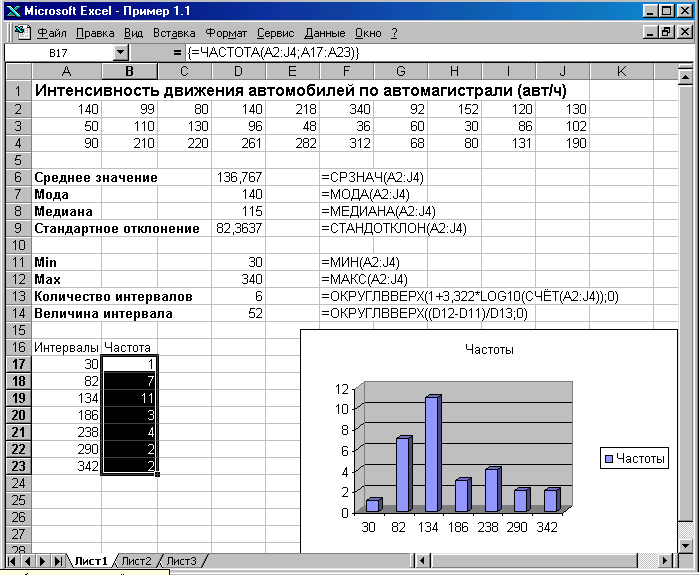
Рис. Использование функций статистической обработки данных.

Использование надстройки «Пакет Анализа»

Для успешного применения процедур анализа, собранных в надстройке необходимы начальные знания в области статистических и инженерных расчетов, для которых эти инструменты были разработаны.

Режим «Описательная статистика» надстройки «Пакет анализа» используется для генерации одномерного статистического отчета, содержащего информацию о центральной тенденции и изменчивости входных данных. Эти сведения необходимы чаще всего для принятия инвестиционных решений.

Одним из важнейших параметров описательной статистики является доверительный интервал.

Доверительный интервал - это интервал, с помощью которого возможна оценка с заданной вероятностью неизвестного значения генеральной совокупности. Это неизвестное значение называется доверительным, а его границы - доверительными границами (верхние и нижние границы).

Рассмотрим использование описательной статистики на примере решения задачи.

Пример.

Из партии электроламп произведена малая выборка для определения продолжительности службы ламп. Результаты выборки приведены в таблице.

Таблица. Продолжительность службы электроламп.

№ лампы	1	2	3	4	5	6	7	8	9	10
Срок горения, час	1450	1370	1250	1400	1360	1420	1400	1320	1300	1430

На основе приведенных данных требуется определить доверительные интервалы, в которых заключена средняя продолжительность службы ламп всей партии, гарантируя результат с вероятностью 0.99.

Решение.

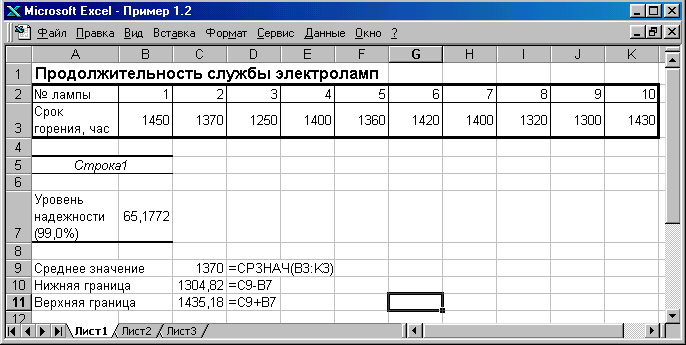Пример решения задачи приведен на рисунке.

Рис. Использование описательной статистики для определения доверительного интервала.

Для решения задачи используем опцию «Описательная статистика» надстройки «Пакет анализа».

В ячейки В3:К3 ввести исходные данные.

Установить курсор в ячейку А5.

Выполнить команду «Сервис/ Анализ данных».

Выбрать опцию «Описательная статистика» и нажать клавишу ОК.

З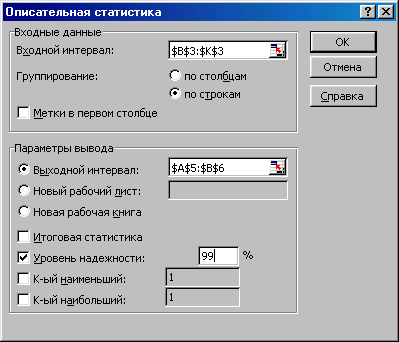 аполнить параметры диалогового окна «Описательная статистика» так, как показано на рисунке.

Рис. Пример заполнения диалогового окна «Описательная статистика»для определения уровня надежности.

Нажать на кнопку ОК. В результате этих действий будет определен уровень надежности с вероятностью 99%.

В ячейке С9 вычислить среднее значение по выборке используя формулу =СРЗНАЧ(B3:K3).

В ячейке С10 определить нижнюю границу доверительного интервала по формуле =C9-B7.

В ячейке С10 определить верхнюю границу доверительного интервала по формуле =C9+B7.

При решении различных задач в диалоговом окне «Описательная статистика» могут быть заданы другие параметры.

Входной диапазон содержит анализируемые данные.

Переключатель Группирование устанавливается в положение По столбцам или По строкам в зависимости от расположения данных во входном диапазоне.

Переключатель Метки в первой строке/Метки в первом столбце устанавливается в положение Метки в первой строке, если первая строка во входном диапазоне содержит названия столбцов, в положение - Метки в первом столбце, если названия строк находятся в первом столбце входного диапазона. Если входной диапазон не содержит меток, то необходимые заголовки в выходном диапазоне будут созданы автоматически.

Флажок Уровень надежности надо установить, если в выходную таблицу необходимо включить строку для уровня надежности. В поле ввести требуемое значение. Например, значение 95% вычисляет уровень надежности среднего со значимостью 0.05.

Флажок К-ый наибольший надо установить, если в выходную таблицу необходимо включить строку для k-го наибольшего значения для каждого диапазона данных. В соответствующем окне введите число k. Если k равно 1, эта строка будет содержать максимум из набора данных.

Флажок К-ый наименьший надо установить, если в выходную таблицу необходимо включить строку для k-го наименьшего значения для каждого диапазона данных. В соответствующем окне введите число k. Если k равно 1, эта строка будет содержать минимум из набора данных.

В поле Выходной диапазон надо ввести ссылку на левую верхнюю ячейку выходного диапазона. Этот инструмент анализа выводит два столбца сведений для каждого набора данных. Левый столбец содержит метки статистических данных; правый столбец содержит статистические данные. Состоящий их двух столбцов диапазон статистических данных будет выведен для каждого столбца или для каждой строки входного диапазона в зависимости от положения переключателя Группирование.

Переключатель Новый лист устанавливается, чтобы открыть новый лист в книге и вставить результаты анализа, начиная с ячейки A1. Если в этом есть необходимость, введите имя нового листа в поле, расположенном напротив соответствующего положения переключателя.

Переключатель Новая книга устанавливается, чтобы открыть новую книгу и вставить результаты анализа в ячейку A1 на первом листе в этой книге.

Флажок Итоговая статистика надо установить, если в выходном диапазоне необходимо получить по одному полю для каждого из следующих видов статистических данных: Среднее, Стандартная ошибка (среднего), Медиана, Мода, Стандартное отклонение, Дисперсия выборки, Эксцесс, Асимметричность, Интервал, Минимум, Максимум, Сумма, Счет, Наибольшее (#), Наименьшее (#), Уровень надежности.

6. Содержание отчета:

   1. Наименование работы.

   2. Цель работы.

   3. Описание решения задач в электронных таблицах Microsoft Excel.

   4. Описание решения задач в истеме математической обработки данных MathCad.

   5. Выводы по работе.

7. Контрольные вопросы:

   1. В чем заключается суть статистической обработки данных эксперимента?

   2. Какие функции статистической обработки используются для описательной статистики?

   3. Что называется доверительным интервалом?

   4. Что такое интервальное распределение?