2.3 Уравнения движения электропривода

Наиболее удобным методом составления уравнений движе­ния механической части привода являются уравнения Лагранжа второго рода. При этом предполагается, что движение механической части исследуется в системе обобщенных коорди­нат, в качестве которых должны быть приняты независимые пара­метры, определяющие положения механизма. Такими параметра­ми являются углы поворота вращающихся вокруг неподвижных осей дискретных инерционных элементов q_t и их линейные пере­мещения S_i (рис. 2.11).

Рис. 2.11 Расчетные схемы механической части:

а - для вращающихся элементов; б - для поступательно движущихся элементов

Уравнение Лагранжа второго рода

, (2.28)

где - кинетическая энергия системы ;

- потенциальная энергия системы;

–работа сил рассеяния (диссипативная функция Релея);

- обобщенная координата;

- обобщённая скорость;

- обобщённая внешняя сила, соответствующая обобщённой координате.

При вращательном движении , ;

;

при поступательном движении , ,

.

Число уравнений Лагранжа второго рода для системы равно числу дискретных инерционных элементов, т.е. числу степеней свободы механизма.

Для механической системы, содержащей n инерционных и n 1 упругих элементов:

или ; (2.29)

или ; (2.30)

или . (2.31)

Моменты (силы), входящие в левую часть уравнения Ла­гранжа (2.28) и действующие на 1-й инерционный элемент системы, определяются как

1)инерционные

(2.32)

где =;

2)потенциальные

; (2.33)

; (2.34)

3) диссипативные

; (2.35)

. (2.36)

Для =1 (для первой массы)

. (2.37)

Производная (момент)

Для =2

. (2.39)

Производная (момент)

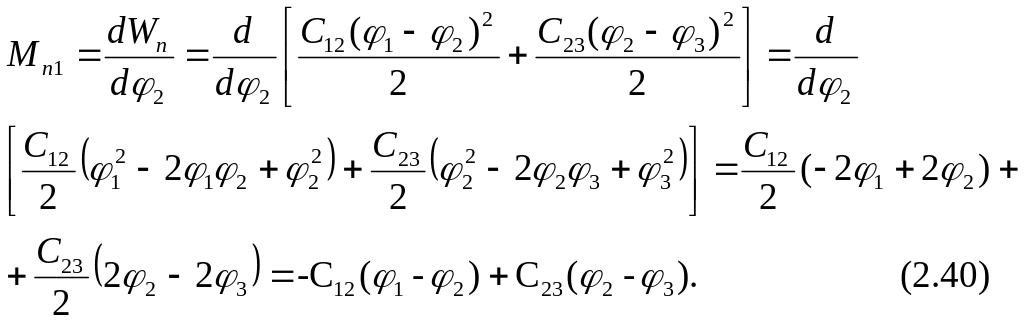
В соответствии с уравнением Лагранжа (2.28) для любого - гo звена может быть записано уравнение движения

; (2.41)

, (2.42)

где , - суммарный внешний момент (сила), действующий на -ое звено.

В тех случаях, когда момент инерции (масса) звена не зависит от его положения, =0 , получим

; (2.43)

= , (2.44)

где , – угловое и линейное ускорение.

Диссипативные силы в упругих связях, обусловленные сила­ми вязкого трения, существенно меньше потенциальных сил, в связи с чем при исследовании законов движения электроприводов механизмов в первом приближении их можно не учитывать.

С учетом указанных допущений уравнения движения в слу­чае трехмассовой системы имеют следующий вид

(2.45)

Для двухмассовой системы

(2.46)

С учётом, что момент упругой связи , уравнения 2.46 запишутся в следующем виде

(2.47)

Для одномассовой абсолютно жесткой системы на основа­нии (2.32) при J = var можно записать уравнение движения

, (2.48)

а при = const

. (2.49)

2.4. Механические переходные процессы электропривода

Переходные процессы в электроприводе возникают при пе­реходе из одного установившегося состояния к другому, когда из­меняются скорость, момент, ток двигателя. Внешней причиной возникновения этих процессов являются управляющие и возму­щающие воздействия: изменения питающего напряжения, его час­тоты, нагрузки на валу, момента инерции, магнитного потока, со­противлений в цепях двигателей и т.д.

Реакция привода на возмущающее или управляющее воз­действия составляет суть переходных процессов. Внутренней при­чиной, обусловливающей переходные процессы, являются инер­ционности электропривода - механическая и электромагнитная.

Изменение запаса кинетической энергии и электромагнитной энергии в элементах его электрических цепей происходит во времени, что объясняет возникновение переходных процессов даже при скачкообразном изменении управляющих и возмущающих воздействий.

В качестве простейших примеров рассмотрим ряд переходных процессов в механической части электропривода, представленной жёстким механическим звеном ( см. рис. 2.10, в).

Переходные процессы при М = const, М_с = const, J = const

В соответствии с уравнением движения электропривода

в механической части электропривода действуют два момента: электромагнитный момент двигателя М и момент статических сопротивлений М_с, приведенный к валу двигателя. Результатом их взаимодействия является динамический момент

.

Для определенности математического описания движения электропривода одно из двух возможных направлений вращения двигателя принимается за положительное. Тогда, если на рас­сматриваемом интервале времени направления момента и скоро­сти двигателя совпадают, т.е. момент и скорость имеют одинако­вые знаки, то работа совершается за счет двигателя (двигатель­ный режим). В противном случае, когда знаки момента и скорости различны, двигатель потребляет механическую энергию с вала (тормозной режим). Таким образом, в уравнении движения элек­тропривода перед М может стоять знак «+» или «-» .

Момент статистических сопротивлений имеет разную приро­ду: реактивные моменты всегда противодействуют движению, ак­тивные моменты могут препятствовать или способствовать движе­нию, т.е. перед М_с может стоять знак «-» или «+». Тогда уравне­ние движения электропривода одномассовой системы с учетом знаков моментов может быть записано в виде

. (2.50)

Знак и величина динамического момента являются резуль­татом взаимодействий М и М_с. В связи с чем , различают сле­дующие режимы работы электропривода

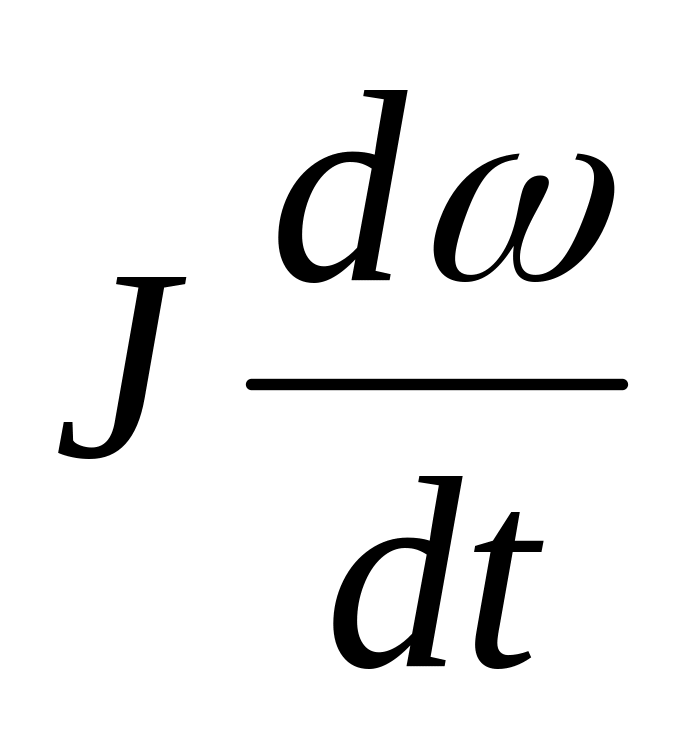1. М_дин > 0, т. е. , что соответствует разгону двигателя при > 0 и торможению двигателя при < 0;

2. М_дин <0, т.е. 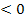, что соответствует торможе­нию при >0 и разгону при <0;

3. _Мдин = 0, т.е. =0, что соответствует установившемуся режиму при =const.

На рис. 2.12 приводятся зависимости , , , на различных этапах движения механической части электропривода:при реактивном М_с (рис. 2.12, а) и активном М_с (рис. 2.12,б), М_n =М_m .

Как видно из приведенных графиков, на всех этапах пере­ходных процессов М_n =М_m, М_с = const, тогда как динамиче­ские моменты при пуске и торможении различны. Самостоятельно предлагается проанализировать движение механической части, когда на всех этапах движения (кроме уста­новившегося, где М_дин = 0) М_дин = const.

Определение времени пуска, торможения, свободного выбега и перемещения

Решая уравнение движения (2.50) относительно производной скорости, получим

, (2.51)

где - ускорение (замедление) привода.

Проинтегрировав (2.51)

получим время переходного процесса изменения скорости от до

. (2.52)

Рис. 2.12,а. Схема движения, идеализированные механические характеристики = f(М) и кривые М = f(t), = f(t)

при реактивном моменте статического сопротивления М_с

Рис. 2.12,б. Схема движения, идеализированные механические характеристики = f(М) и кривые М = f(t), = f(t)

при активном моменте статического сопротивления М_с

При равенстве ускорение = 0 , привод осущест­вляет установившееся движение при ( ).

В общем случае время пуска и торможения найдётся по уравнению

. (2.53)

Величина динамического момента определяет время переходных процессов при пуске и торможении. Следует отметить, что при реактивном

при ,

а при активном моменте

при ,

тогда как в режиме пуска на опускание груза и в режиме торможения при подъёме груза

при .

Следует отметить, что если, например, задан количественно пусковой и , то время пуска

, (2.54)

т.е. при заданной пусковой мощности время пуска будет определяться двойным запасом кинетической энергии привода

. (2.55)

В связи с этим с целью экономии электрической энергии, потребляемой из сети, и потерь энергии в электроприводе нужно проектировать электропривод с минимальным запасом кинетической энергии.

В режимах торможения с целью уменьшения потерь энергии в приводе оно должно осуществляться с нагрузкой. Тогда

; (2.56)

, (2.57)

т.е. пропорционально запасу кинетической энергии при тормозной мощности равной пусковой.

Время свободного выбега привода при

, (2.58)

т.е. практически при заданной мощности холостого хода определяется двойным запасом кинетической энергии привода и является относительно большим.

Угол поворота вала двигателя за время пуска, торможения

. (2.59)

При равноускоренном (замедленном) движении

, (2.60)

где - ускорение (замедление).

Тогда

. (2.61)

При движении с установившейся скоростью

. (2.62)

На рис. 2.13 представлены тахограмма = f(t) и изменение угла поворота за цикл работы механизма.

Рис. 2.13. К расчёту угла поворота вала двигателя