
- •Содержание
- •Введение
- •Содержание задания
- •Рекомендации по выполнению и оформлению домашнего задания.
- •Приложение 1.
- •Приложение 2. Значения функции р(λ)
- •Приложение 3.
- •Семестровое домашнее задание по дисциплине «Статистика» Раздел «Общая теория статистики»
- •1. Проверка первичной информации на однородность, наличие аномальных наблюдений и нормальность распределения
- •2. Вариационный ряд распределения активов банков и система показателей, вычисляемая на его основе
- •2.1. Определение количества групп
- •2.2. Показатели центра распределения
- •2.3. Показатели вариации
- •2.4. Показатели дифференциации
- •Показатели концентрации
- •2.6. Показатели формы распределения
- •2.7. Проверка соответствия эмпирического распределения внешнеторгового оборота фирм нормальному распределению с помощью критериев согласия Пирсона, Романовского и Колмогорова
- •3. Определение доверительного интервала для средней величины внешнеторгового оборота фирм в генеральной совокупности
- •4. Анализ зависимости таможенных платежей от внешнеторгового оборота фирм
- •4.2. Проверка правила сложения дисперсий и оценка степени влияния факторного признака на величину результативного.
- •4.4. Построение уравнения парной регрессии
- •4.4.1. Статистический анализ модели
- •4.4.2. Оценка качества построенной модели
- •Характеристики точности
- •Проверка адекватности модели
- •4.4.3. Построение доверительных интервалов
2.7. Проверка соответствия эмпирического распределения внешнеторгового оборота фирм нормальному распределению с помощью критериев согласия Пирсона, Романовского и Колмогорова
Критерий Пирсона
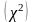
 (37)
(37)
где — эмпирические частоты (частости) в интервале;
 — теоретические
частоты (частости) в интервале.
— теоретические
частоты (частости) в интервале.
Значения теоретических частот (графа 9 табл. 2) рассчитаны с помощью функции плотности нормального распределения ОКРУГЛ(n*h*НОРМ.РАСП(X, Среднее, Стандартное – откл, Интегральный);0),
где n=48 – объём выборки;
h=69,92 – ширина интервала;
X – средние значения ВТО в интервалах, (графа 2 табл. 2);
Среднее = 72,29;
Стандартное_ откл = 82,592;
Интегральный = 0 - логическое значение, определяющее форму функции (ноль соответствует плотности распределения);
0 – количество знаков после запятой в функции округления.
Расчётное значение
критерия сравнивается с критическим
 ,
которое определено с помощью функции
ХИ2ОБР(0,05; 2) EXCEL,
где 0,05 - уровень значимости, а 2 - количество
степеней свободы для данного примера.
Формула = ХИ2ОБР(0,05; 2) рассчитывает
значение 5,99, задающее правостороннюю
критическую область (5,99; +∞). Так как
выполняется условие
,
которое определено с помощью функции
ХИ2ОБР(0,05; 2) EXCEL,
где 0,05 - уровень значимости, а 2 - количество
степеней свободы для данного примера.
Формула = ХИ2ОБР(0,05; 2) рассчитывает
значение 5,99, задающее правостороннюю
критическую область (5,99; +∞). Так как
выполняется условие
 ,
то отклонения теоретических частот от
эмпирических являются случайными и
распределение ВТО фирм не противоречит
нормальному.
,
то отклонения теоретических частот от
эмпирических являются случайными и
распределение ВТО фирм не противоречит
нормальному.
Критерий Романовского
 ,
(38)
где
,
(38)
где
 - число степеней свободы;
- число степеней свободы;
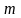 —
число групп;
—
число групп;
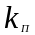 —количество
параметров в теоретическом законе
распределения (для нормального закона
распределения
—количество
параметров в теоретическом законе
распределения (для нормального закона
распределения );
);
В данном примере расчётное значение меньше 3, следовательно можно принять гипотезу о нормальном характере эмпирического распределения.
Критерий Колмогорова ( )
Основан на определении максимального (по модулю) расхождения между накопленными частотами эмпирического и теоретического распределений (d) ,графа 11 табл. 2:
 .
(39)
.
(39)
По известному
значению
определяется вероятность
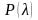 (П.2 табл. 1), если она близка к 1, то
расхождение между частотами случайны.
(П.2 табл. 1), если она близка к 1, то
расхождение между частотами случайны.
График эмпирических и теоретических частот приведен на рис. 3.
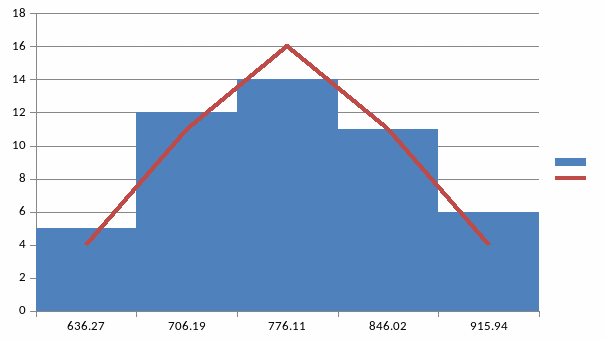
Рис.3 График эмпирических и теоретических частот
Анализ результатов расчета позволяет сделать следующие выводы:
В качестве характеристики центра распределения необходимо использовать среднюю арифметическую, т.к. совокупность является однородной (коэффициент вариации равен 10,62%, что менее 33%).
Степень дифференциации ВТО фирм слабая.
Концентрация ВТО фирм практически отсутствует.
Распределение ВТО фирм плосковершинно и имеет правостороннюю асимметрию. Отклонения эмпирических частот от теоретических носят случайный характер, следовательно, эмпирическое распределение ВТО фирм не противоречит нормальному.
3. Определение доверительного интервала для средней величины внешнеторгового оборота фирм в генеральной совокупности
Величина доверительного интервала (предельная ошибка выборки) находится из выражения
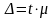 ,
(40)
,
(40)
где t – коэффициент доверия;
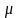 - средняя ошибка
выборки.
- средняя ошибка
выборки.
Средняя ошибка бесповторной выборки:
 ,
(41)
,
(41)
где
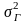 - дисперсия генеральной совокупности;
- дисперсия генеральной совокупности;
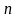 - объем выборочной
совокупности;
- объем выборочной
совокупности;
N – объём генеральной совокупности.
В случае малой выборки (n<100) средняя ошибка бесповторной выборки находится из выражения:
 (42)
(42)
где

Коэффициент доверия в распределении Стьюдента является функцией доверительной вероятности и функцией объема выборки. Его значение получим с помощью функции СТЬЮДРАСПОБР (1-0,9973; 47), где 1-0,9973 – уровень значимости, n-1=47- количество степеней свободы.
 .
.
Выборка считается репрезентативной, если величина ее относительной ошибки составляет не более 5%, т.е.
 (43)
(43)
Учитывая, что
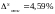 ,
выборку следует признать представительной.
,
выборку следует признать представительной.
