Производная показательной функции.

Вывод формулы производной приведем на основе определения:

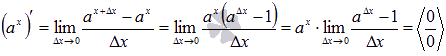
Пришли к неопределенности. Для ее раскрытия введем новую переменную  , причем   при  . Тогда  . В последнем переходе мы использовали формулу перехода к новому основанию логарифма.

Выполним подстановку в исходный предел:

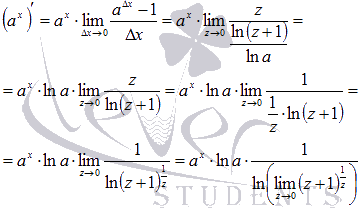
Если вспомнить второй замечательный предел, то придем к формуле производной показательной функции:

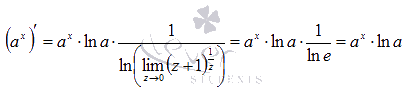
Пример.

Найти производные показательных функций  .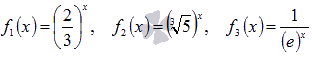

Решение.

Воспользуемся доказанной выше формулой производной показательной функции из таблицы и свойствами логарифма.

Производная логарифмической функции.

Докажем формулу производной логарифмической функции для всех x из области определения и всех допустимых значениях основания a логарифма. По определению производной имеем:

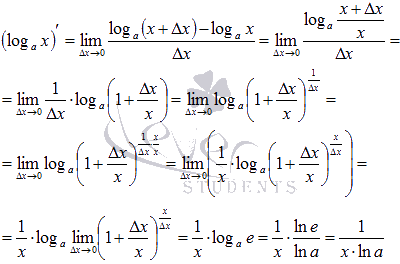
Как Вы заметили, при доказательстве преобразования проводились с использованием свойств логарифма. Равенство 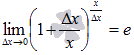  справедливо в силу второго замечательного предела.

Пример.

Вычислить производные логарифмических функций  .

Решение.

Формулу мы уже вывели, так давайте ею и воспользуемся (в первом случае основание логарифма равно натуральному логарифму трех a = ln3, во втором a = e):

Таким образом, производная натурального логарифма равна единице деленной на x.

Производные тригонометрических функций.

Для вывода формул производных тригонометрических функций нам придется вспомнить некоторые формулы тригонометрии, а также первый замечательный предел.

По определению производной для функции синуса имеем  .

Воспользуемся формулой разности синусов:

Осталось обратиться к первому замечательному пределу:

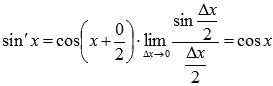
Таким образом, производная функции sin x есть cos x.

Абсолютно аналогично доказывается формула производной косинуса.

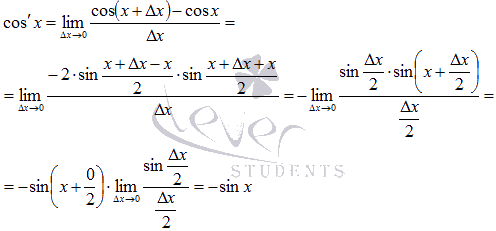
Следовательно, производная функции cos x есть –sin x.

Вывод формул таблицы производных для тангенса и котангенса проведем с использованием доказанных правил дифференцирования (производная дроби).

Производные обратных тригонометрических функций.

Доказательство формул производных арксинуса, арккосинуса, арктангенса и арккотангенса подробно рассмотрено в разделе производная обратной функции, поэтому не будем повторяться.

Производные гиперболических функций.

Правила дифференцирования и формула производной показательной функции из таблицы производных позволяют вывести формулы производных гиперболического синуса, косинуса, тангенса и котангенса.

6) Геометрический смысл производной

Тангенс угла наклона касательной прямой

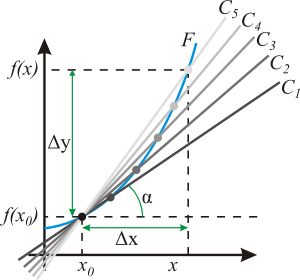
Геометрический смысл производной. На графике функции выбирается абсцисса x₀ и вычисляется соответствующая ордината f(x₀). В окрестности точкиx₀ выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C₅). Расстояние Δx = x — x₀ устремляется к нулю, в результате секущая переходит в касательную(постепенно темнеющие линии C₅ — C₁). Тангенс угла α наклона этой касательной — и есть производная в точке x₀.

Если функция   имеет конечную производную в точке   то в окрестности   её можно приблизить линейной функцией

Функция   называется касательной к   в точке   Число   является угловым коэффициентом или тангенсом угла наклона касательной прямой.

Скорость изменения функции

Пусть   — закон прямолинейного движения. Тогда   выражает мгновенную скорость движения в момент времени   Вторая производная   выражает мгновенное ускорение в момент времени 

Вообще производная функции   в точке   выражает скорость изменения функции в точке  , то есть скорость протекания процесса, описанного зависимостью 

Уравнение касательной и нормали к графику функции в точке

Уравнение касательной

Пусть функция задается уравнением y=f(x), нужно написать уравнение касательной в точке x0. Из определения производной: 

y/(x)=limΔx→0ΔxΔy

Δy=f(x+Δx)−f(x). 

Уравнение касательной к графику функции: y=kx+b (k,b=const). Из геометрического смысла производной: f/(x0)=tgα=k  Т.к. x0 и f(x0)∈  прямой, то уравнение касательной записывается в виде: y−f(x0)=f/(x0)(x−x0) , или

y=f/(x0)·x+f(x0)−f/(x0)·x0. 

 

 

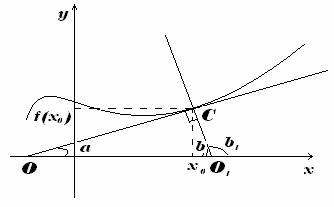
Уравнение нормали

Нормаль - это перпендикуляр к касательной (см. рисунок). Исходя из этого:

tgβ=tg(2π−α)=ctgα=1tgα=1f/(x0)

Т.к. угол наклона нормали -- это угол β1, то имеем:

tgβ1=tg(π−β)=−tgβ=−1f/(x).

Точка (x0,f(x0))∈  нормали, уравнение примет вид:

y−f(x0)=−1f/(x0)(x−x0).

Экономический смысл производной заключается в следующем: производная является важнейшим инструментом экономического анализа, позволяющим углубить геометрический и математический смысл экономических понятий, а также выразить ряд экономических законов с помощью математических формул. С ее помощью решаются важнейшие экономические задачи. На практике производная служит очень хорошим инструментом при решении задач оптимизационного характера: на производительность труда, эластичность спроса и др. Из этого следует вывод, что производная играет важную роль в экономике.

 

.

Геометрический смысл производной. На графике функции выбирается абсцисса x₀ и вычисляется соответствующая ордината f(x₀). В окрестности точкиx₀ выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C₅). Расстояние Δx = x — x₀ устремляется к нулю, в результате секущая переходит в касательную(постепенно темнеющие линии C₅ — C₁). Тангенс угла α наклона этой касательной — и есть производная в точке x₀.