аВопросы к экзамену по математическому анализу

1. Понятие предела функции является одним из самых важных в математике. Дадим два определения этому понятию.

Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε > 0 существует δ > 0 такое, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x) – A| < ε.

Определение предела по Гейне. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для любой последовательности   такой, что   сходящейся к числу a, соответствующая последовательность значений функции  сходится к числу A.

Если для функций f(x), g(x) существуют постоянные c>0, >0, такие, что |f(x)| c |g(x)| при |x-a|<, x a, то говорят, что f является ограниченной по сравнению с функцией g в окрестности точки a и пишут, что f(x) = O(g(x)) при x a.

Данное определение переносится и на случай, когда x, x.

1. Так как |1/x²|  |1/x| при |x|  1, то 1/x² = O(1/x) при x ;

2. 1/x = O(1/x²) при x 0 так как |1/x| 1/x² при |x| 1.

Запись f=O(1) при x a означает, что функция f(x) ограничена в некоторой окрестности точки a.

Теорема о локальной ограниченности функции, имеющей предел.

Если у функции в данной точке существует конечный предел, то в некоторой проколотой окрестности данной точки функция ограничена

НЕПРЕРЫВНОСТЬ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ

Перечислим элементарные функции.

1. Р(х) — многочлен, Р(х) = а_ох^п + ... + а_п.

2. Рациональная функция f(x) = Q(x)/P(x), где Р(х), Q(x) — многочлены.

3. Показательная функция f(x) = а^х, а> 0, а ^ 1.

4. Степенная функция f(x) = х^а = e^alnx.

5. Логарифмическая функция f(x) = log_a х, а > 0, а ** 1.

6. Все тригонометрические функции.

7. Всевозможные суперпозиции всех этих функций.

Эти функции называют элементарными потому, что только их рассматривают в рамках элементарной математики. Отвлекаясь от строгих определений и опираясь на основные функциональные свойства, докажем не­прерывность показательной функции у = а^х и функции у = sin x.

УТВЕРЖДЕНИЕ 2. При любом х₀ е R функция у = а^х непрерывна.

► Пусть а > 1. Тогда надо доказать, что для любого е > 0 сущест­вует 8 = 8(е) > 0 такое, что при всех х с условием \х — х_о\ < 5 име­ем \а^х - а^хо\ < е, или, что то же самое, |а^х~^х° - 1| < га~^х«= г_г. Заме­тим, что можно ограничиться случаем г_г < 1. В качестве 8(е) возьмем число 8_г = S^Sj) > 0 такое, что из неравенства \х - х_о\ < 8_г следует неравенство \а^х~^х° - 1| <е_г. Далее положим 8(е) = 5₁(е₁) =

8j < х - х₀ < 6_Х. Так как а > 1, то

"^§1

Сначала докажем, что а ^х — 1 < е_г. Положим

Тогда I/Si > N, т. е. 6_Х < 1/N. Так как

(1 + е₁)^ЛГ> 1 + 8₁Л^>1 + е₁-

^£i

то

Отсюда следует, что

a⁵i - 1 < е,, a"⁵i> —-— = 1 - ^£l > 1 - s,. ¹ 1+г_х 1+г_х ^J

Окончательно имеем

-Sj < a"⁵i - 1 < а^х~^х° - 1 < a⁵i - 1 < 8j,

следовательно, |a^x~^x<> - 1| < Sj. Тем самым доказана непрерыв­ность f(x) = а^х в точке х₀. <

УТВЕРЖДЕНИЕ 3. Функция f(x) = sin x непрерывна в точке х₀. ► Вспомним, что Isin х\ < |х|. Тогда имеем

|sm х - sm x_o| =

X Х

2sm——— cos

<2

х - х,

=\х -

Таким образом, для любого е > 0 положим 8(е) = е, и получим |sin х — sin х_о| < е V х: \х — х_о\ < е.

Следовательно, функция f(x) = sin x непрерывна. < Эти утверждения можно записать так:

sin х = sin x₀ + а(х), а^х = а^х° + Р(х),

где а(х), Р(х) — бесконечно малые функции.

Оказывается, что при х —» 0, т. е. при х₀ = 0, имеют место бо­лее точные соотношения, которые называются замечательными пределами:

sinx -, е^х -1 -, ------ ~ 1, -------- ~ 1.

X X

Эти пределы используются далее для изучения дифференциаль­ных свойств элементарных функций.

2).

Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю.

Применение первого замечательного предела на практике

Задание. Найти предел 

Решение. Воспользуемся заменой и первым замечательным пределом.

2. 

3. 

Ответ. 

Задание. Найти предел 

Решение. Разложим тангенс на синус и косинус и воспользуемся свойствами пределов.

4. 

5. 

6. 

Ответ. 

Следствия из первого замечательного предела

Следствия

• 

• 

• 

• 

Доказательство следствий  

3). Бесконечно малая — числовая функция или последовательность, которая стремится к нулю.

Бесконечно большая — числовая функция или последовательность, которая стремится к бесконечности определённого знака.

Последовательность   называется бесконечно малой, если  . Например, последовательность чисел   — бесконечно малая.

Функция называется бесконечно малой в окрестности точки  , если  .

Функция называется бесконечно малой на бесконечности, если   либо  .

Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если  , то  ,  .

Последовательность   называется бесконечно большой, если  .

Функция называется бесконечно большой в окрестности точки  , если  .

Функция называется бесконечно большой на бесконечности, если   либо  .

• Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.

• Если   — бесконечно малая последовательность, сохраняющая знак, то 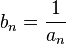  — бесконечно большая последовательность.