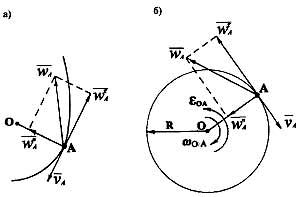
3.2.1. Направления скоростей и ускорений точек звеньев механизма

В общем случае криволинейного движения вектор скорости точки А (рис 3.1, а), как и вектор тангенциальной составляющей полного ускорения, направлены по касательной к траектории движения, а вектор нормальной составляющей полного ускорения – вдоль нормали (отсюда название составляющей) к касательной по направлению к центру кривизны траектории О. В частном случае, когда траекторией является окружность, (рис. 3.1, б), то векторы и перпендикулярны радиусу ОА, а вектор направлен параллельно ОА от точки А к центру окружности О. В том случае, если ОА – звено механизма и известны его угловая скорость ω_ОА и угловое ускорение ε_ОА, то:

= ωОА LOA; = εОА LOA; = .

(3.6)

Вектор направлен в сторону вращения, т.е. совпадает с направлением угловой скорости ω_ОА. Направление вектора совпадает с направлением углового ускорения ε_ОА.

В случае поступательного прямолинейного движения радиус кривизны траектории ОА равен бесконечности, следовательно = 0, и полное ускорение точки А будет равно тангенциальной составляющей.

Рис. 3.1. Направления скорости

и ускорения криволинейного движения

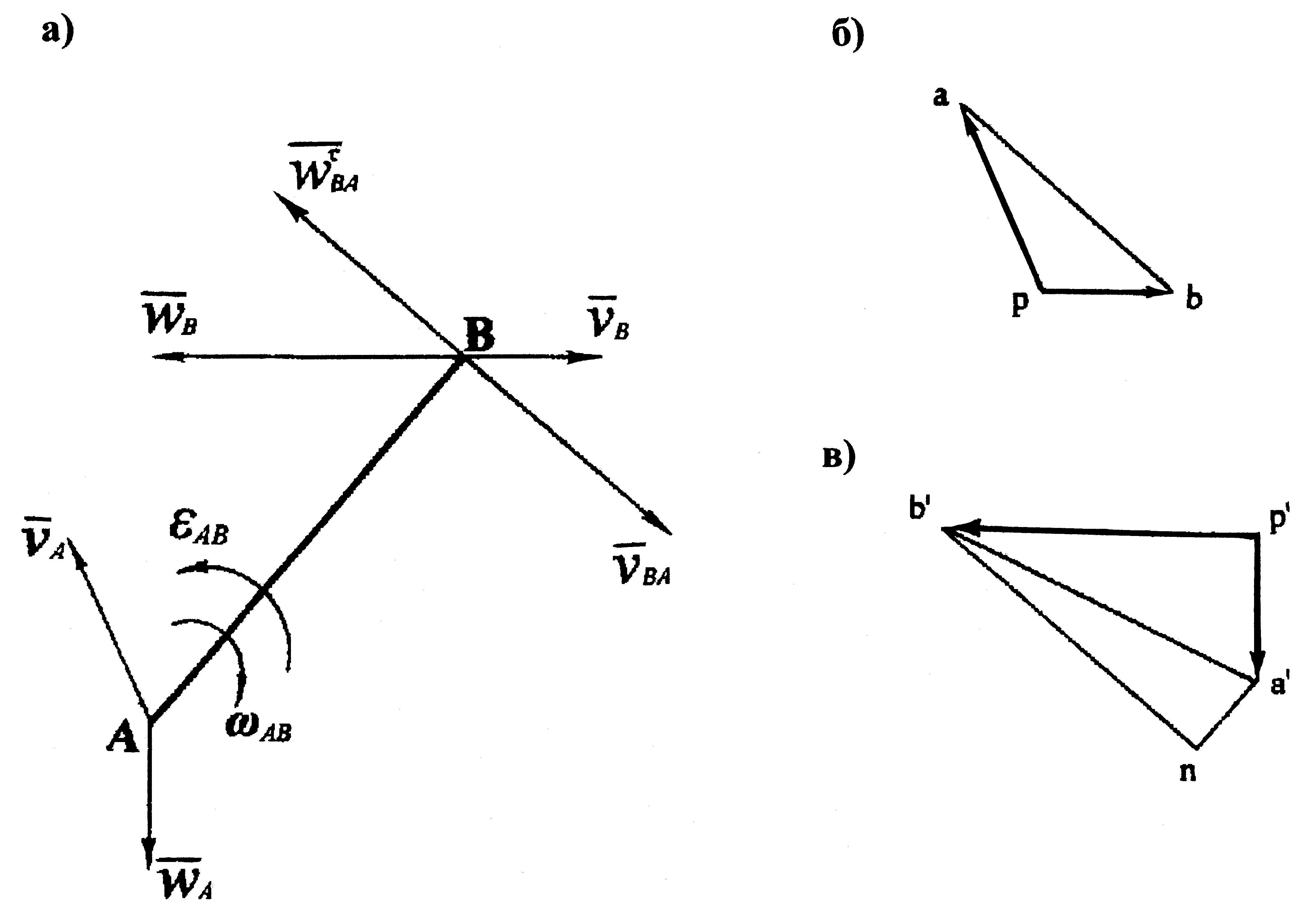
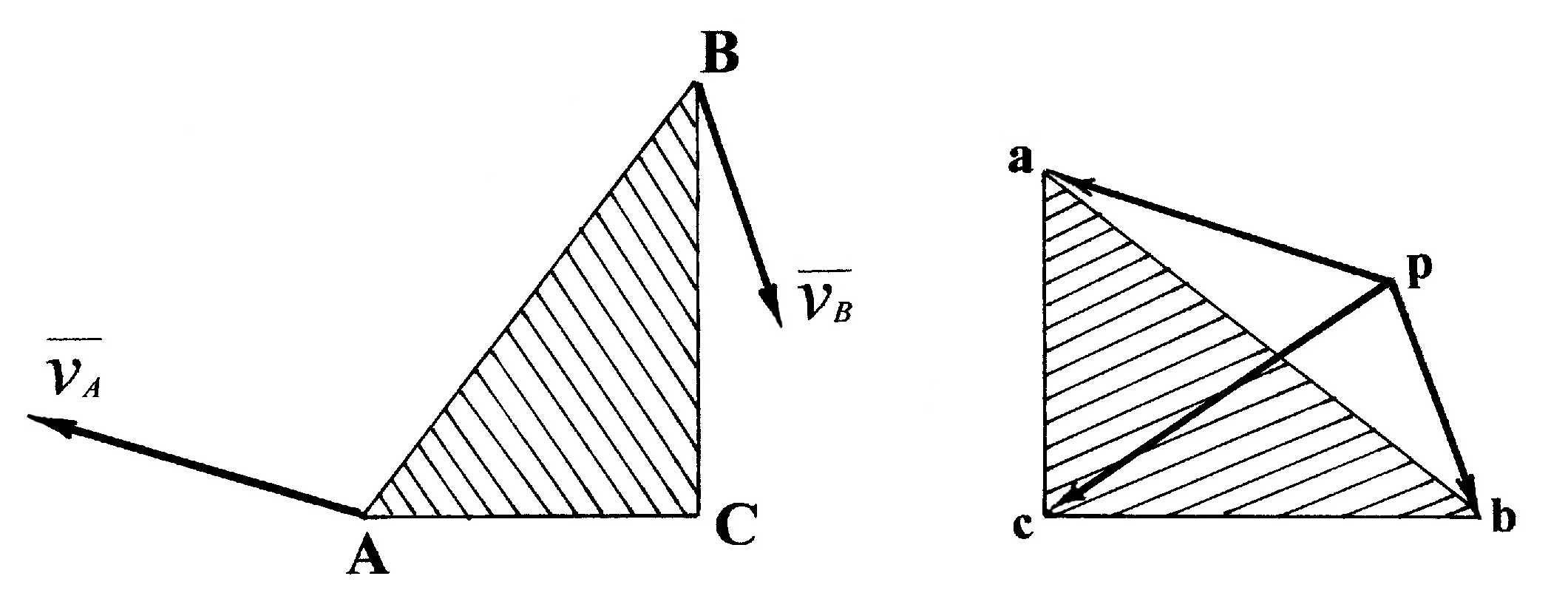
Если для любого звена построены план скоростей и план ускорений, то можно определить направления и величины угловой скорости и углового ускорения. Пусть для звена АВ (рис. 3.2, а) построены план скоростей (рис. 3.2, б) и план ускорений (рис. 3.2, в) точек А и В.

Рис. 3.2. Определение угловой скорости

и углового ускорения звена АВ

Перенесем в точку В звена вектор относительной скорости точки В, снятый с плана скоростей ( = k_{v *} аb) и вектор тангенциальной составляющей полного ускорения, снятый с плана ускорений ( = k_w nb'). Направления векторов и определят соответственно направления угловой скорости ω_АВ и углового ускорения ε_АB.

ωАВ = ; εАB = .

(3.7)

3.2.2. Определение скоростей и ускорений точек звеньев методом подобия

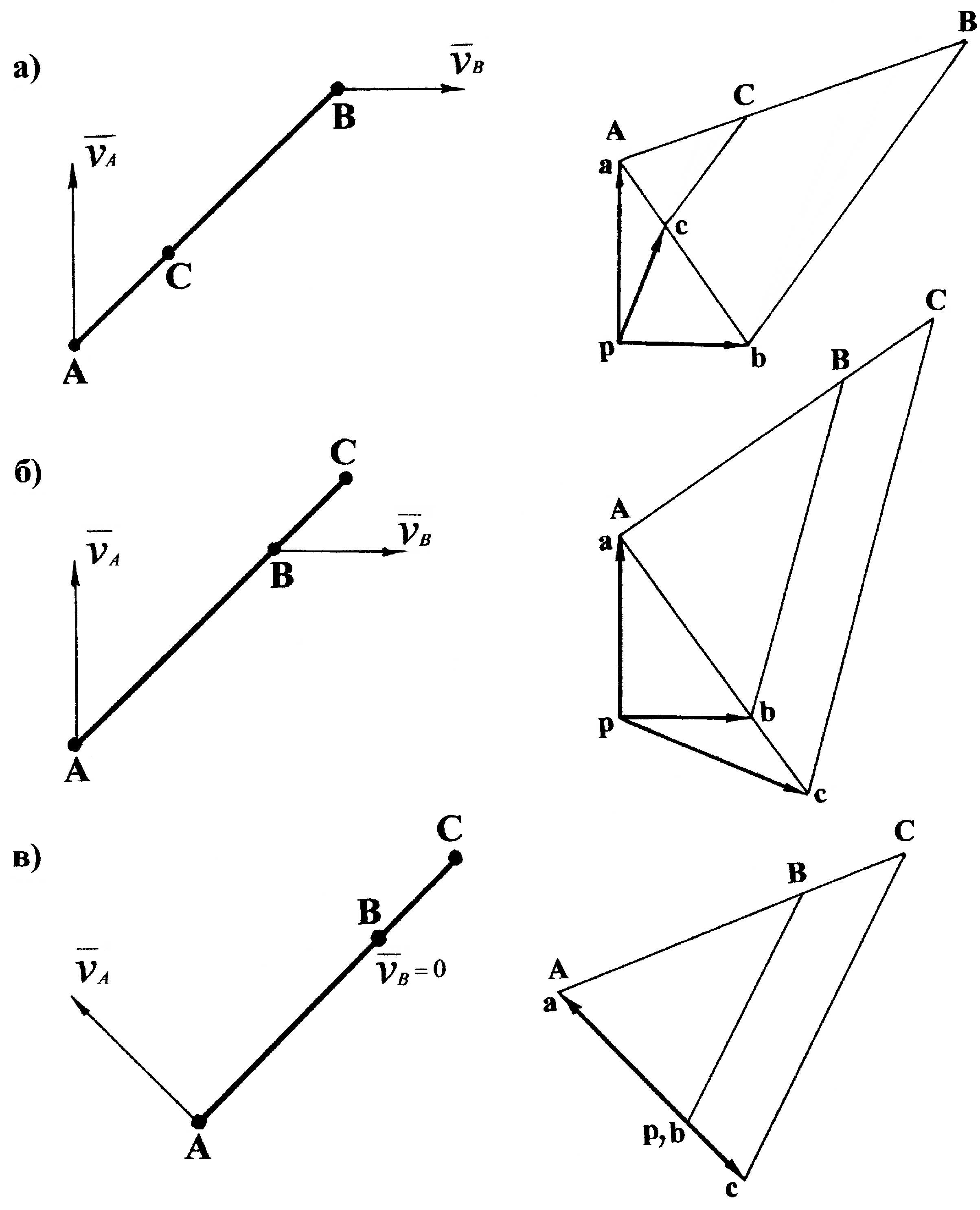
Если известны скорости и ускорения двух точек звена, то, применяя метод подобия, можно определить скорость и ускорение любой точки этого звена. Поясним на примере скоростей точек.

Например, чтобы определить модуль и направление вектора скорости точки С звена АВ, если известны параметры векторов скоростей точек А и В (рис. 3.3, а), достаточно на отрезке аb плана скоростей найти точку с, которая делит аb в том же отношении, что и точка С делит звено АВ. Для этого отрезок АВ перенесем на план скоростей, совмещая точку А с точкой а, затем соединим точку В с точкой b и проведем через точку С прямую, параллельную Вb до пересечения с аb в искомой точке с. Тогда отрезок рс будет изображать вектор абсолютной скорости точки С.

На рис. 3.3, б, в приведены варианты расположения искомой точки С на звене АВ.

Рис. 3.3. Графическое определение скоростей точек звена,

лежащих на одной прямой

Если точка С не лежит на прямой АВ или на ее продолжении, то на отрезке аb плана скоростей необходимо построить треугольник аbс, подобный треугольнику АВС звена, причем треугольник аbс нельзя переворачивать в плоскости чертежа, т.е. последовательность обхода вершин треугольников аbс и АВС в одном направлении (или по часовой стрелке или против часовой стрелки) должна быть одинакова. Полученный в результате построений отрезок рс (рис. 3.4) выражает скорость точки С.

Рис. 3.4. Графическое определение скоростей точек звена,

не лежащих на одной прямой

Методом подобия можно определять и ускорения точек звеньев механизмов при условии, что все вышеприведенные построения необходимо выполнять, разумеется, на плане ускорений звена.

Для определения нормальной составляющей полного ускорения и кориолисова^ (поворотного) ускорения точек звеньев целесообразно использовать графические методы, как более наглядные и практически безошибочные. Для этого, кроме схемы механизма необходимо иметь построенный план скоростей.

Суть метода заключается в следующем: преобразовав известные из теоретической механики аналитические зависимости

и = 2ωпер отн = 2

(3.8)

в пропорции

и ,

(3.9)

где R – радиус кривизны траектории переносного движения;

– скорость относительного движения;

– скорость переносного движения.

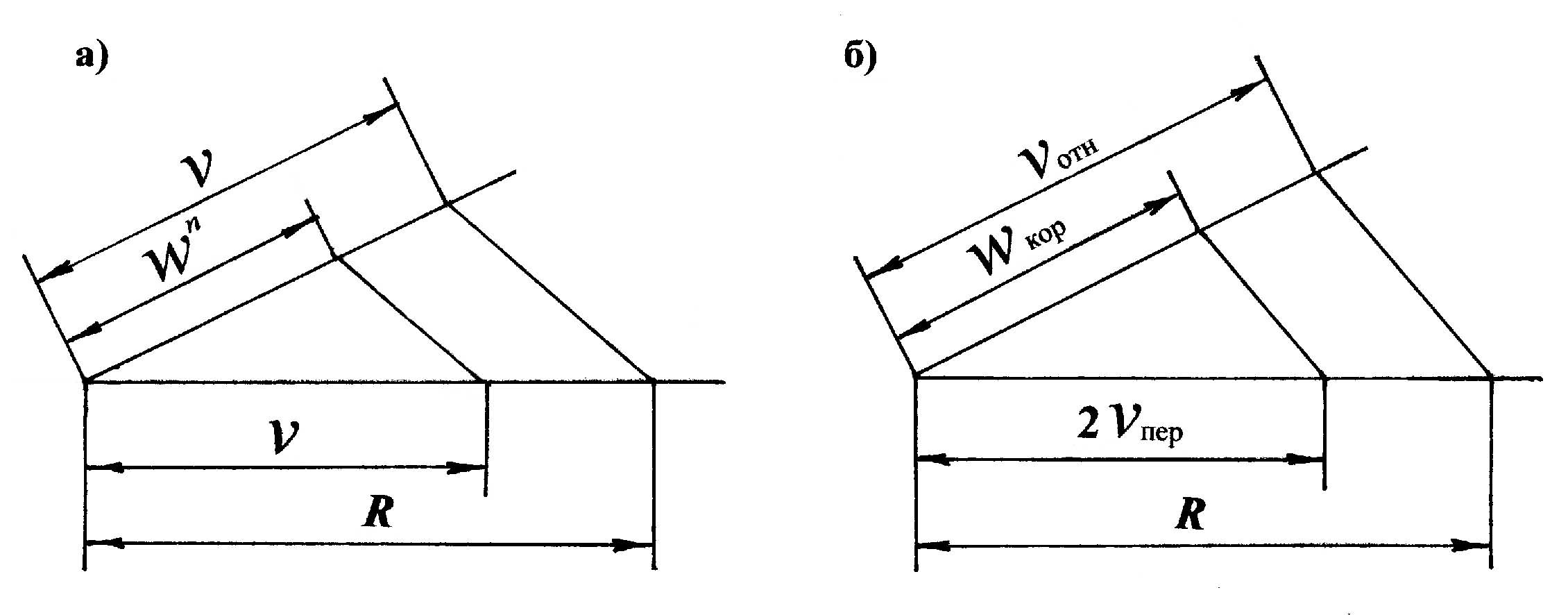
Построив подобные треугольники на сторонах двух лучей, выходящих из одной точки (рис. 3.5), по трем известным величинам (сторонам треугольников) находим неизвестные четвертые – соответственно нормальное (рис. 3.5, а) и кориолисово (рис. 3.5, б) ускорения.

Рис. 3.5. Графический метод определения нормального

и кориолисова ускорений

Для конкретных механизмов или структурных групп все необходимые величины снимаются непосредственно с чертежа, причем не требуется выполнение дополнительных расчетов, что упрощает решение пропорций (3.9). Полученные отрезки, выражающие нормальное (3.10) и кориолисово (3.11) ускорения, сразу переносятся на план ускорений без каких-либо пересчетов.

а'n = ;

(3.10)

p'к = .

(3.11)

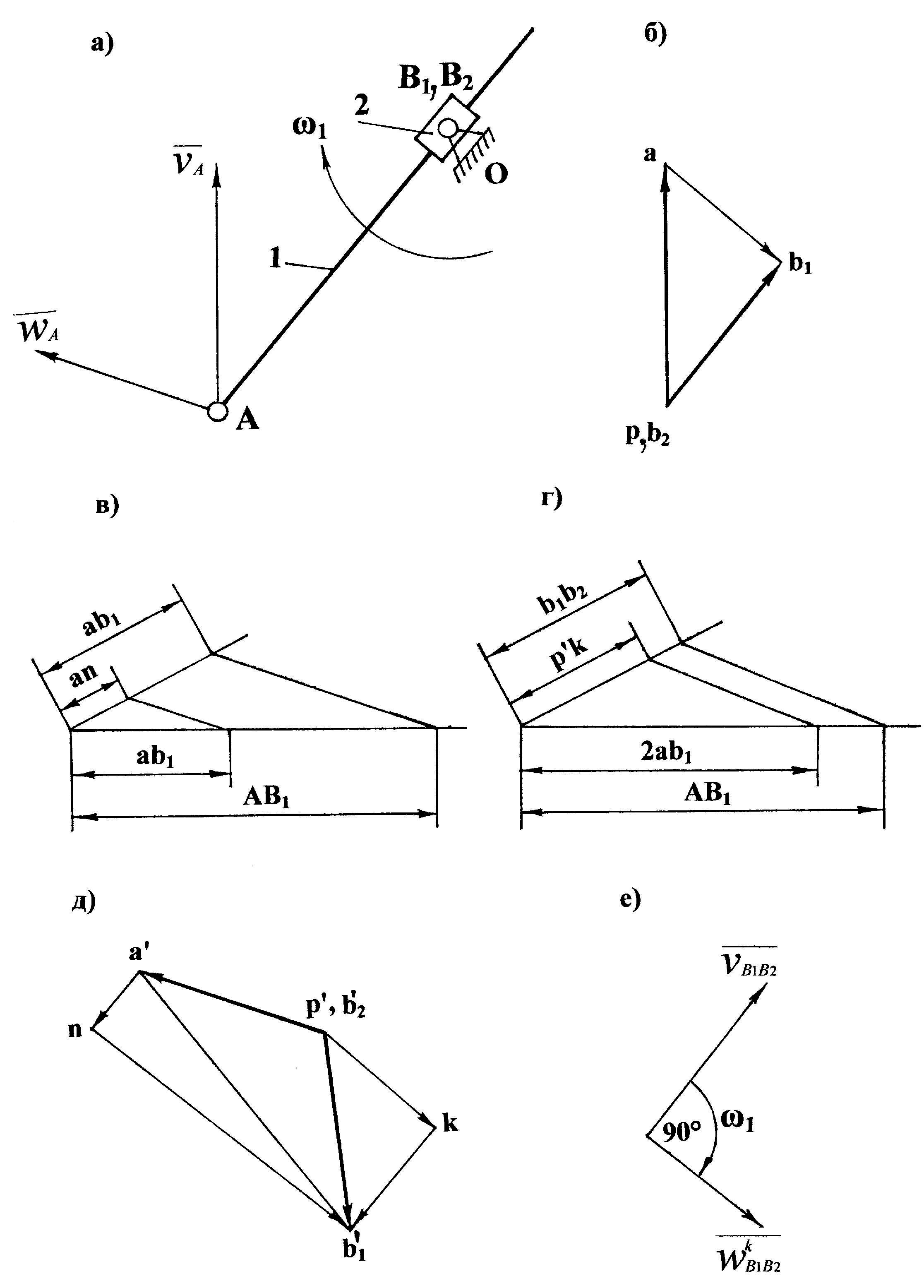
Пример. Пусть требуется построить план ускорений структурной группы 3 вида, состоящей из звеньев 1 и 2, соединенных внутренней поступательной парой в точке В₁ и имеющей две внешние вращательные пары в точках А и В₂ (рис. 3.6, а). Скорость и ускорение точки А (звено 1) известны, скорость и ускорение точки В₂ равны нулю (звено 2 связано вращательной парой со стойкой 0 и поэтому не имеет линейных перемещений). План скоростей группы приведен на рис. 3.6, б. Требуется графическим способом определить ускорение точки В₁ звена 1 (рис. 3.6, е). Из курса теоретической механики [4, 5] известно, что ускорение точки В₁ складывается из ускорения относительного (поступательного) движения точки А, ускорения переносного движения точки В относительно точки А и кориолисова ускорения (подробнее см. в [9]).

Рис. 3.6. Планы скоростей и ускорений структурной группы 3-го вида

На рис. 3.6, в представлена методика определения отрезка, выражающего нормальное ускорение точки В₁ (точки В₁ и В₂ совпадают, но принадлежат разным звеньям). На двух лучах, выходящих из одной точки, построены отрезки в пропорции:

.

(3.12)

На нижнем луче откладываются: отрезок АВ₁ с плана положения группы и отрезок аb₁ с плана скоростей. На верхнем луче откладывается отрезок аb₁.

Соединив В₁ и b₁, проведем линию b₁n, параллельную В₁b₁ до пересечения с верхним лучом в точке n. Отрезок а'n и есть искомый, изображающий в соответствующем масштабе ускорений вектор нормальной составляющей ускорения точки В₁.

На рис. 3.6, г представлено аналогичное построение отрезка p'k, выражающего кориолисово ускорение .

На двух лучах, выходящих из одной точки, построены отрезки в пропорции:

.

(3.13)

Отрезки аb₁ и b₁b₂ снимаются с плана скоростей, отрезок АВ₁ – с плана положения группы. На плане ускорений p'к кb'₁, а а'n кв'₁. Подробная методика и векторные уравнения, необходимые для построения планов скоростей и ускорений разных структурных групп приведены в [9]. Для определения направления вектора кориолисова ускорения необходимо вектор относительной скорости повернуть на 90º в сторону переносного движения, т.е. по направлению угловой скорости звена 1 (рис. 3.6, д).

Более подробно метод планов изложен в [1], [3].

Пример построения планов скоростей и ускорений механизма в заданном положении см. в Приложении.
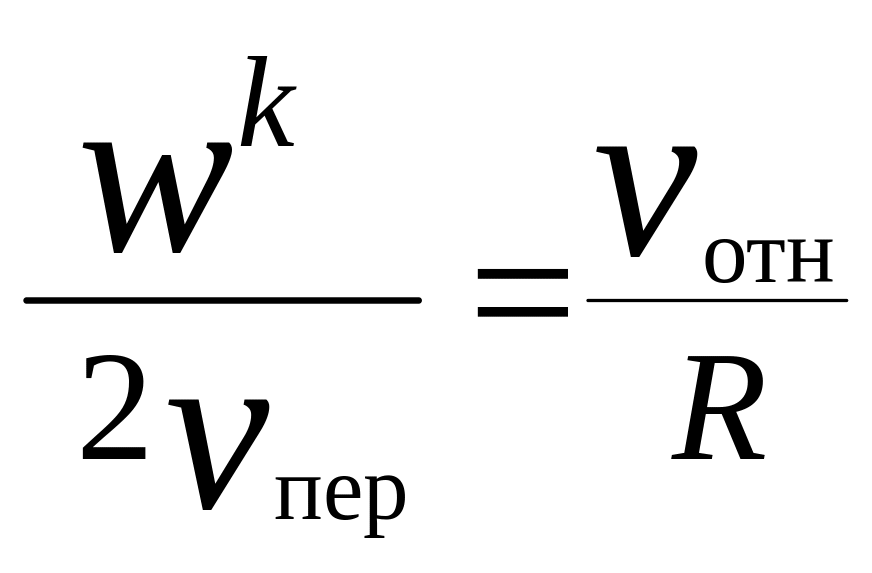