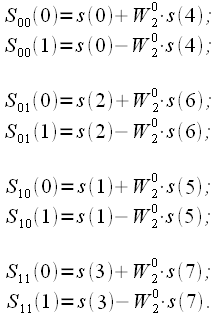1. 2. 1. Швидке перетворення Фур'є (шпф)

Формули (3) і (4) є основою для побудови алгоритму швидкого  перетворення Фур'є (ШПФ). Цей алгоритм за рахунок рекурсивного застосування формули (3) зводить ДПФ вихідної послідовності розмірності n = 2^l , де l є N, до набору 2-точкових перетворень Фур’є.

Отже маємо:

Помножимо x^-_k на W_n^-jk і просумуємо по k = 0 ... (n–1)

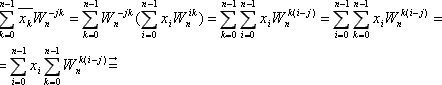
1. 2. 2. Двійково-інверсна перестановка

Наведемо у вигляді графа алгоритм ШПФ із проріджуванням за часом заснований на розбитті - об'єднанні при N=8.

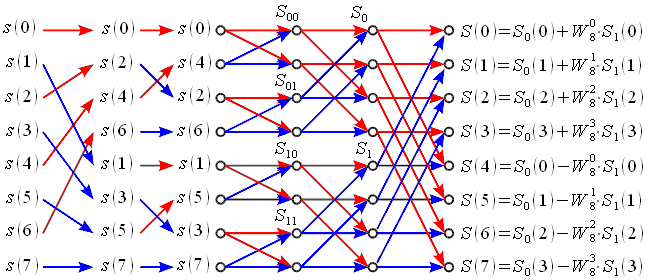
Рис. 2. Граф алгоритму ШПФ з проріджуванням за часом при N = 8

На першому етапі відліки вхідного сигналу переставляються місцями і вихідна послідовність ділиться на “парну” і “непарну” (позначені червоними і синіми стрілками). Потім “парна” і “непарна” послідовності у свою чергу діляться на «парну» і «непарну» послідовності. При N=2^Lтакий розподіл можна робити L-1 разів. У цьому випадку L=3. Дана процедура називається двійково-інверсною перестановкою, так можна виконати перенумерацію відліків переписавши номер відліку в двійковій системі у зворотному напрямку. Наприклад s(4) має індекс у десятковій системі числення 4₁₀ = 100₂, Якщо ж 100₂переписати справа наліво то отримаємо 001₂ , Тобто s(4) після розбиття на парні непарні перед першою операцією «Метелик» стане на місце s(1), яка в свою чергу стане на місце s(4). За аналогічним правилом поміняються місцями всі відліки, при цьому деякі залишаться на місці, зокрема s(2), бо якщо 2₁₀ = 010₂ переписати справа наліво то все одно залишиться 010₂, Аналогічно s(0), s(5) і s(7). Дуже важливо зрозуміти, що даний метод перенумерації повинен застосовуватися при запису числа в двійковій системі, яка складається з L розрядів. У наведеному прикладі використовувалися 3 розряди двійкового числа, але якщо ж L =4 ( N=16), то необхідно записати число при використанні 4 розрядів. У цьому випадку 2₁₀=0010₂ і після переписування отримаємо 0100₂ , Тобто при N=16 s(2) не залишиться на місці, а поміняється місцями з s(4).

Можна сказати що безпосередньо двійково-інверсна перестановка зручна коли наперед кількість відліків вхідного сигналу фіксована, проте в універсальних алгоритмах ШПФ на різні розміри , Двійково-інверсна перестановка не ефективна, простіше і швидше поміняти відліки місцями.

Після двійково-інверсної перестановки отримуємо чотири 2-точкових ДПФ:

	(5)

На основі чотирьох 2-точкових ДПФ формуються два 4-точкових ДПФ:

	(6)

І на останньому рівні формується повний спектр вхідного сигналу.

1. 2. 3. Поворотні коефіцієнти

Розглянемо детальніше поворотні коефіцієнти .

На першому рівні (вираз (5)) потрібно всього один поворотний коефіцієнт , це означає, що на першому рівні спектра, операції множення не потрібні ( множення на ±1 називаються тривіальними, тому що при множенні на ±1, множник залишеється незмінним або змінює свій знак на протилежний).

На другому рівні маємо два поворотних коефіцієнта:

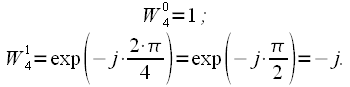(7)

Множення на уявну одиницю також можна вважати тривіальним, тому що дійсні та уявні частини комплексного числа просто міняються місцями і змінюють свій знак.

На третьому рівні маємо вже 4 поворотних коефіцієнта:

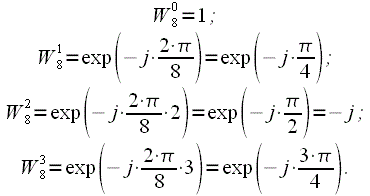(8)

Графічно поворотні коефіцієнти можна представити як вектори на комплексній площині:

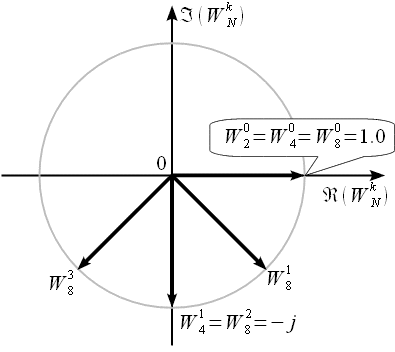
Рис. 3. Поворотні коефіцієнти алгоритму ШПФ з проріджуванням за часом при N = 8

Можна відмітити, що на всіх рівнях об’єднання кількість поворотних коефіцієнтів подвоюється, причому всі поворотні коефіцієнти попереднього рівня об’єднання присутні і на наступному рівні. Таким чином для того, щоб перейти на наступний рівень необхідно між поворотними коефіцієнтами поточного рівня вставити поворотні коефіцієнти наступного. Графічно для переходу на наступний рівень при N = 16 необхідно доповнити рисунок 3, як це показано на рисунку 4.

Сірі вектора показують поворотні коефіцієнти які будуть присутні на останньому рівні при N = 16, яких немає при N = 8.

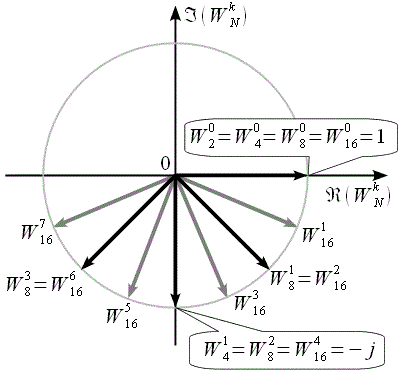
Рис. 4. Поворотні коефіцієнти алгоритму ШПФ з проріджуванням за часом при N = 16

Необхідно також відзначити, що всі поворотні коефіцієнти за винятком нульового , перебувають у нижній півплощині комплексної площини.