1. Теоретичний розділ

1. 1. Характеристики процесора adsp-bf516f

1. 1. 1. Властивості процесора adsp-bf516f

Особливості

– Ядро ADSP-BF516 з частотою до 400 МГц;

– Два 16-розрядних помножувача;

– Два 40-розрядних АЛП;

– Чотири 8-розрядних відео АЛП;

– 40-розрядний пристрій зсуву;

Пам’ять

– 116Кб пам’ять на кристалі;

– Зовнішній контролер пам'яті з безклєєвою підтримкою SDRAM і і асинхронними 8-розрядною і 16-розрядною пам’ятями;

– Пам’ять ОТР (One-time-programmable);

– Додаткова 4Мб на кристалі SPI Flash з опцією завантаження;

– Захист коду з технологією безпеки Lockbox;

Периферія

– Паралельний периферійний інтерфейс (PPI);

– Послідовні порти (SPORT);

– Послідовний периферійний інтерфейс (SPI);

– Таймери загального призначення;

– Універсальний асинхронний приймач-передавач (UART);

– Годинник реального часу (RTC);

– Порт введення / виведення загального призначення (програмовані

прапорці);

1. 1. 2. Опис процесора adsp-bf516f

Процесор ADSP-BF516F являє собою процесор сімейства Blackfin з розширеними можливостями, тобто володіє більшою продуктивністю і меншою споживаної потужністю в порівнянні з попередніми процесорами сімейства Blackfin при збереженні простоти використання і сумісності коду. Архітектура ядра процесора Blackfin є архітектурою з єдиним набором команд, що включає ядро обробки сигналів із подвійним блоком множення-накопичення, що має ортогональний набір команд, характерний для RISC - мікропроцесорів, що володіє гнучкістю команд типу SIMD і мультимедійними можливостями. Особливістю продуктів сімейства Blackfin є динамічне управління живленням. Можливість зміни, як напруги живлення, так і робочої частоти дозволяє оптимізувати споживання потужності відповідно з конкретним завданням.

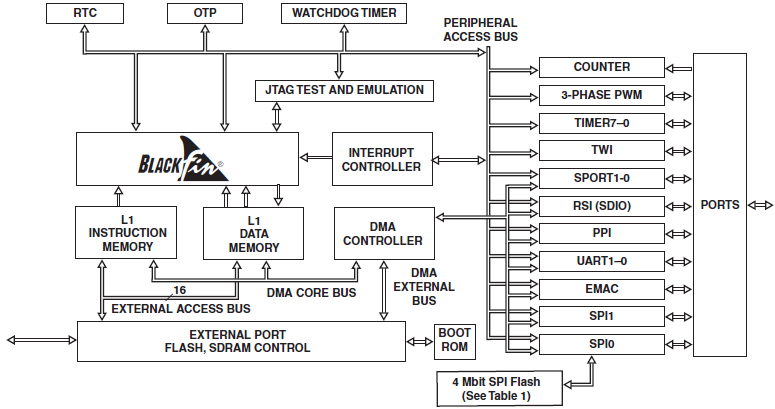
Рис. 1. Функціональна блок-діаграма процесора

1. 2. Опис алгоритму шпф з прорідженням у часі

Дискретним перетворенням Фур'є над вихідною послідовністю чисел {x₀, x₁, …, x_n-1} потужністю n є N, n> 1, де x_i є Z, i = (0, n-1), наз. таке перетворення, в результаті якого виходить послідовність {x’₀, x’₁ , ..., x_n-1} комплексних чисел x_k тієї ж потужності, кожен елемент якої рахується за правилом:

де  k = (0, n-1), W = e^-j*π/n і де j – уявна частина

Існують такі W^ik, в яких (ik) рівні. Неважко помітити, що для виконання n-точкового перетворення Фур'є необхідно виконати n (n–1) комплексних додавань та (n–1) (n–1) комплексних множень (з урахуванням, що W⁰ = 1 ). При цьому множник W^ik буде використаний стільки разів, скільки дільників з діапазону (0, n-1) у показника степеня (ik). Маємо:

Оскільки sin α = – sin (α + π), cos α = – cos (α + π), то:

(1)

Звідки випливає, що:

(2)

Таким чином, діапазон ступенів (ik) за допомогою формули (1) скорочується з (0, (n–1) (n–1) ), до (0, n-1), а за допомогою формули (2) – до (0, n/2–1).

Нехай n - довжина вихідної послідовності чисел {x₀,x₁,…,x_n-1} парна, тоді перетворення Фур’є для такої послідовності можна записати у вигляді:

(3)

З урахуванням формули (1), а також виразу

формулу (3) часто записують у вигляді:

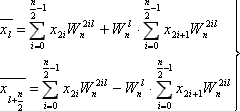(4)

Розглянемо першу суму формули (3). Поклавши n/2 = m, отримаємо:

1)	n = 2m;
2)	;
3)	.

Аналогічні міркування можна провести і відносно другої суми формули (3). Таким чином, ДПФ вихідної послідовності розмірністю n=2m зводиться до двох ДПФ послідовностей розмірністю m чисел кожна, складених з парних і не парних елементів вихідної послідовності.