Аналіз режиму роботи лінії електропередавання за заданими потужністю і напругою в кінці без врахування зарядної потужності лінії

1. Мета роботи

Основною метою роботи є дослідження режиму роботи лінії електропередавання за заданими параметрами режиму в кінці лінії без врахування зарядної потужності.

6.2 Основні теоретичні відомості

Розрахунок режиму симетричної трифазної лінії місцевої мережі з рівномірним навантаженням фаз (рисунок 6.1, а) здійснюють на підставі однофазної схеми заміщення, зображеної на рисунку 6.1,б.

Фазну напругу на початку лінії визначимо за другим законом Кірхгофа як

, (6.1)

де - фазна напруга в кінці лінії;

- струм навантаження лінії;

- повний опір лінії.

Розглянемо векторну діаграму лінії (рисунок 6.1, в). Для активно-індуктивного навантаження вектор відстає від вектора напруги на деякий кут φ₂. Вектор спаду напруги на активному опорі лінії збігається за фазою зі струмом , а вектор спаду напруги на індуктивному опорі – випереджує цей струм на 90°. Додавши до вектора спади напруг на активному та індуктивному опорах згідно з виразом (6.1), отримаємо вектор фазної напруги на початку лінії.

Напруга відрізняється за величиною від напруги і зміщена відносно останньої на кут δ.

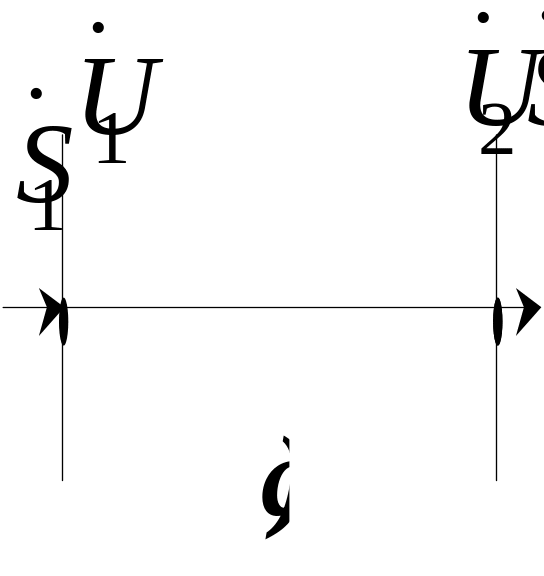
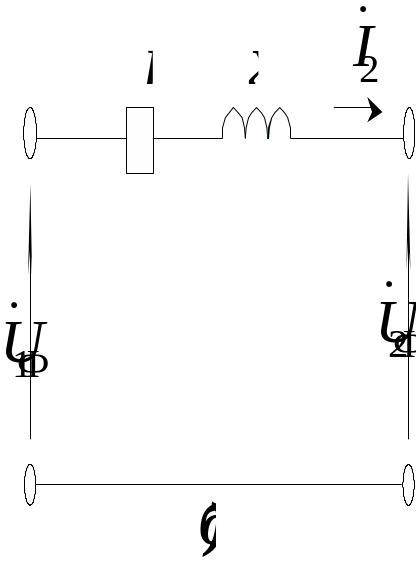
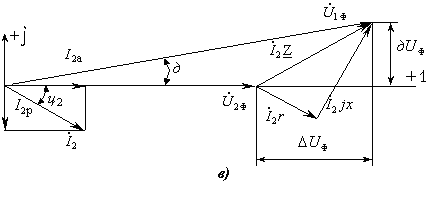
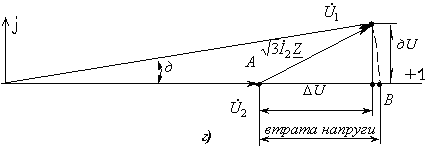
а - однолінійна схема; б - схема заміщення; в - векторна діаграма фазних напруг; г - векторна діаграма лінійних напруг

Рисунок 6.1 - Схеми і векторні діаграми лінії місцевої мережі

Вектор ,, який дорівнює геометричній різниці векторів і , називають спадом напруги в лінії. Алгебричну різницю абсолютних значень цих напруг називають втратою напруги.

Розклавши вектор спаду напруги на поздовжню і поперечну складові, можна записати

, (6.2)

де , (6.3)

, (6.4)

І_2а, І_2р - відпововідно активна й реактивна складові струму навантаження .

У більшості випадків навантаження лінії задають трифаз­ною активною Р₂ і реактивною Q₂ потужностями. При переході від фазних до лінійних напруг, врахувавши, що

, (6.5)

отримаємо

, (6.6)

. (6.7)

Модуль лінійної напруги на початку лінії визначимо з векторної діаграми (рисунок 6.1, г) за теоремою Піфагора

. (6.8)

Кут зсуву фаз між векторами напруг і визначимо згідно з рисунком 1.1, г як

. (6.9)

Втрати активної та реактивної потужності в трифазній лінії можна розрахувати за формулами

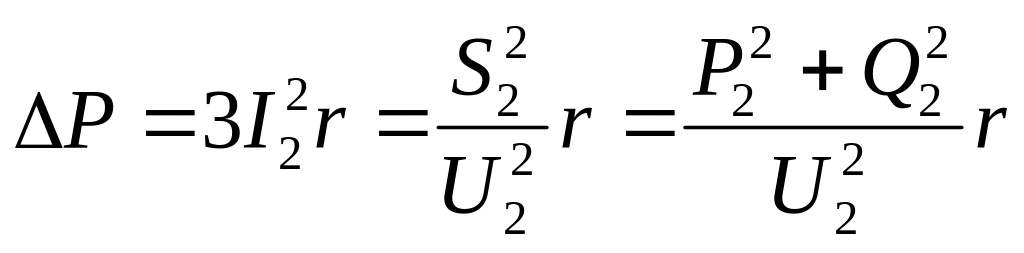, (6.10)

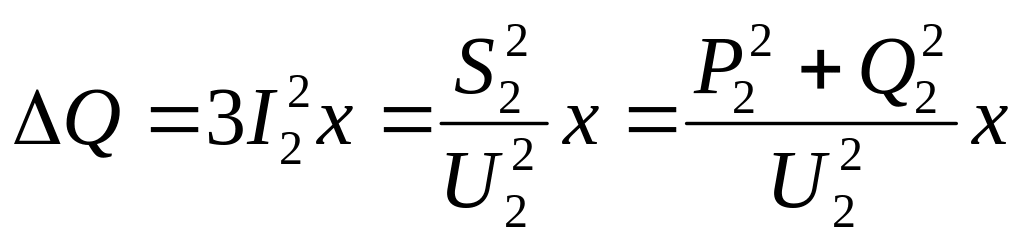. (6.11)

Потужність на початку лінії визначимо з рівняння балансу потужностей як

. (6.12)

Коефіцієнт корисної дії лінії

…………………………………………………………………..

6.3 Порядок виконання роботи

1. Ознайомтеся з основними теоретичними відомостями.

2. Визначіть, користуючись довідником, питомі параметри лінії r₀, x₀, b₀ для заданого варіанта вихідних даних (таблиця 6.1).

3. Розрахуйте режим роботи лінії вручну та на комп’ютері без врахування ємнісної провідності.

4. Побудуйте в масштабі векторні діаграми фазних і лінійних напруг лінії.

4. Визначте коефіцієнт корисної дії лінії.

Таблиця 6.1 – Вихідні дані до лабораторної роботи №6

Варіант	Довжина лінії, км	Марка проводу	U2, кВ	Потужність навантаження
				P2, МВт	Q2, Мвар
1	35	АС-150	110	27	15
2	40	АС-185	110	20	12
3	90	АС-240	220	80	60
4	125	АС-300	220	108	65
5	40	АС-185	110	25	15
6	100	АС-300	220	90	50
7	45	АС-150	110	28	16
8	50	АС-185	110	26	20
9	120	АС-240	220	100	56
10	105	АС-300	220	125	86
11	60	АС-240	110	22	12
12	140	АС-400	220	120	60
13	44	АС-120	110	34	24
14	35	АС-150	110	30	18
15	150	АС-400	220	125	70
16	117	АС-240	220	100	60
17	45	АС-150	110	32	20
18	145	АС-300	220	110	50
19	122	АС-400	220	135	70
20	43	АС-185	110	35	18
21	125	АС-240	220	95	42
22	39	АС-120	110	28	14
23	55	АС-240	110	26	14
24	130	АС-300	220	108	56
25	136	АС-400	220	122	68
26	37	АС-95	110	18	16
27	135	АС-300	220	115	70
28	34	АС-120	110	34	21
29	42	АС-150	110	24	18
30	118	АС-240	220	105	40