4.4 Дислокации

Дислокация – это дефекты кристаллического строения, представляющие собой линии, вдоль и вблизи которых нарушено характерное для кристалла правильное расположение атомных плоскостей. Дислокации - это перемещения.

Различают два вида дислокаций: краевую и винтовую. Краевая дислокация (рис24).

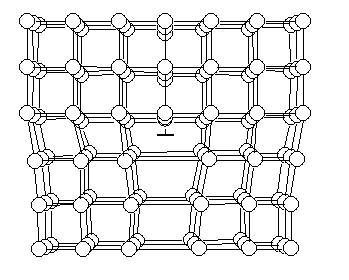
рис. 24 рис. 25

Искажение кристаллической структуры вызвано тем, что, и части объёмного кристалла в процессе его роста возникла лишняя атомная «полуплоскость». Искажения сосредоточено в основном вблизи нижнего края «полуплоскости» «лишних» атомов. Под дислокацией в подобных случаях понимают линию, проходящую вдоль края лишней атомной «полуплоскости».

Искажение сосредоточено вблизи дислокационной линии. На расстоянии же нескольких атомных диаметров в сторону искажения настолько малы, что в этих местах кристалл имеет почти совершенную форму. Искажения возле края «лишней полуплоскости» вызваны тем, что ближайшие атомы как бы «пытаются» согласовать своё расположение с резким обрывом «лишней полуплоскости».

Любая царапина на поверхности кристалла может стать причиной краевой дислокации. Действительно, царапину на поверхности кристалла можно рассматривать как нехватку одной атомной плоскости. В результате теплового движения атомы из соседних областей могут перейти на поверхность, а дислокация тем самым переместится во внутрь.

Другой тип дислокаций был описан Бюргерсом, и получил название винтовая дислокация. Винтовая дислокация (рис 25).

Винтовая дислокация получена при помощи частичного сдвига по плоскости Q вокруг линии EF (рис. 1.3). На поверхности кристалла образуется ступенька, проходящая от точки Е до края кристалла. Такой частичный сдвиг нарушает параллельность атомных слоев, кристалл превращается в одну атомную плоскость, закрученную по винту в виде полого геликоида вокруг линии EF, которая представляет границу, отделяющую часть плоскости скольжения, где сдвиг уже произошел, от части, где сдвиг не начинался. Вдоль линии EF наблюдается макроскопический характер области несовершенства, в других направлениях ее размеры составляют несколько периодов. Если переход от верхних горизонтов к нижним осуществляется поворотом по часовой стрелке, то дислокация правая, а если поворотом против часовой стрелки – левая. Винтовая дислокация не связана с какой-либо плоскостью скольжения, она может перемещаться по любой плоскости, проходящей через линию дислокации. Вакансии и дислоцированные атомы к винтовой дислокации не стекают. Образования винтовой дислокации можно представить таким образом. Мысленно надрежем кристалл по плоскости и сдвинем одну его часть относительно другой по этой плоскости на один период решётки параллельно краю надреза. При этом линия искажения пойдёт вдоль края разреза. Эту линию и называют винтовой дислокацией. При винтовой дислокации лишнего ряда атомов нет. Искажение пространственной решётки кристалла состоит в том, сто атомные ряды изгибаются и меняют своих соседей.

Установлено, что винтовые дислокации чаще всего образуются во время роста кристалла. Однако приложение напряжений может увеличить число винтовых дислокаций.

Дислокации, как и точечные дефекты, могут перемещаться по кристаллической решётке. Однако движение дислокаций связано с большими ограничениями, так как дислокация всегда должна быть непрерывной линией. Возможны два основных вида движений дислокаций: переползание и скольжение. Переползание дислокаций происходит благодаря добавлению или удалению атомов из лишней полуплоскости, что бывает вследствие диффузии. При скольжении дислокации, лишняя полуплоскость, занимавшая определённое положение в кристаллической решётке соединяется с атомной плоскостью, находящейся под плоскостью скольжения, а соседняя атомная плоскость становится теперь лишней полуплоскостью. Такое плавное скольжения линии дислокации вызывается действием напряжений сдвига, приложенных к поверхности кристалла.

Наблюдения показывают, что перемещение дислокаций в реальном кристалле в одних случаях может быть облегчённо, в других – затруднённо, в зависимости от характера тех искажений, которые вносит дислокация в кристаллическую решётку.

Линии дислокаций не могут обрываться внутри кристалла. Они должны либо быть замкнутыми, образуя петлю, либо разветвляться на несколько дислокаций. Либо выходить на поверхность кристалла. Дислокационная структура материала характеризуется плотностью дислокаций. Плотность дислокаций в кристалле определяется как среднее число линий дислокаций, пересекающих внутри тела площадку площадью 1 м², или как суммарная длина линий дислокаций в объеме 1 м³. Плотность дислокаций изменяется в широких пределах и зависит от состояния материала. Плотность дислокации в значительной мере определяет пластичность и прочность материала (рис. 1.4). Минимальную прочность определяет критическая плотность дислокаций. Дислокации влияют не только на прочность и пластичность, но и на другие свойства кристаллов. С увеличением плотности дислокаций возрастает внутреннее сопротивление, изменяются оптические свойства, повышается электрическое сопротивление металла. Дислокации увеличивают среднюю скорость диффузии в кристалле, ускоряют старение и другие процессы, уменьшают химическую стойкость.

Влияние дислокации и других дефектов на механические свойства материалов и на процесс деформирования Изучение дефектов кристаллов имеет важное практическое значение, так как механические свойства твёрдых тел, их пластичность, сопротивление деформированию связаны с дислокациями и другими дефектами в кристаллах.

Экспериментальное изучение механических свойств материалов показывает, что чистые металлы в большинстве являются мягкими и пластичными. Пластичность кристаллов, их относительно малая прочность определяется возникновением дислокаций в процессе роста кристалла. При группировке точечных дефектов образуются микротрещины. Хрупкое разрушение происходит в том случае, если пластическое течение затруднено в виду затруднения дислокаций микротрещинами и другими дефектами, присутствующими в исходном состоянии и возникающими в процессе деформации.

В практике обращает на себя внимания и такой вид разрушений, как усталостное. Усталость-это вид разрушения материала, происходящих в течение продолжительного времени под действием периодически изменяющихся нагрузок при таких напряжениях, которые не приводят к разрушению при статических нагрузках.

В настоящее время хорошо известны основные особенности усталости и меры, которые должны быть приняты для предотвращения её появления. Острые надрезы и переходы на поверхности, отверстия под заклёпки, царапины, коррозия приводят к заметному снижению усталостной прочности машин. Хорошее качество поверхности и защита от коррозии способствует увеличению сопротивления усталости. Однако, несмотря на наличие таких эффективных средств исследования, как электронная микроскопия, многое в механизме усталости остаётся неясным. Усталость является особенно серьёзной проблемой для металлов и сплавов, так как эти материалы широко используются в машинах и конструкциях, подвергающихся действию периодически меняющихся нагрузок.

Итак, на прочность кристаллических материалов влияют дислокации, их движение и взаимодействие, а также другие дефекты, встречающиеся в кристаллах.

Образование дислокаций в кристалле

Чтобы в идеальном кристалле образовалась дислокация, необходимо произвести сдвиг в некоторой части плоскости скольжения. Для этого нужно приложить силу. В реальности рассчитывается не сила, а величина – прочность сдвига в совершенном кристалле, или скалывающее напряжение.

Рассмотрим прямоугольную решетку (рис. 3.16) [74]. Пусть x – смещение, соответствующее приложенному напряжению . При смещении одной атомной цепочки относительно другой в решетке возникают препятствующие смещению напряжения . Эти напряжения стремятся восстановить нарушенное равновесии уменьшают химическую стойкость.

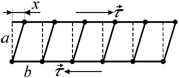
Рис. 3.16. Сдвиг прямоугольной решетки

В силу симметрии решетки , если , где . Решетка оказывает сопротивление приложенному напряжению при и , если .

Этим условиям удовлетворяет синусоидальный закон:

,

(3.14)

где k – постоянная величина.

Величина коэффициента k определяется из закона Гука. При малых смещениях , поэтому

.

(3.15)

С другой стороны, для малых смещений выполняется закон Гука:

,

(3.16)

где G – модуль сдвига. Поэтому можно записать

.

(3.17)

Отсюда

.

(3.18)

Максимальное сопротивление сдвигу, как следует из выражения (3.14), возникает при . Следовательно, коэффициент k есть не что иное, как максимальное сопротивление сдвигу. Эту величину принимают за теоретическую прочность кристалла на сдвиг:

.

(3.19)

Для кристаллов, в которых отношение периодов решетки b/a составляет около 0,6 критическое скалывающее напряжение, рассчитанное по формуле (3.19), должно составлять . Теоретическое число, полученное при учете межатомных взаимодействий в плоскости скольжения, дает несколько меньшее значение . Вместе с тем, экспериментальные измерения показывают, что сдвиг в большинстве реальных кристаллов начинается при значительно меньших напряжениях . Это связано с тем, что сдвиг в кристаллах происходит не путем смещения одних атомных плоскостей относительно других, а путем скольжения дислокаций, имеющихся в кристалле. Часто дислокации в кристалле появляются уже на стадии его роста. Получить кристаллы, не содержащие дислокации, очень сложно. Даже в совершенных кристаллах их плотность (число дислокаций, пересекающих единичную площадку внутри кристалла) достигает , а в сильно деформированных металлических кристаллах может достигать . В настоящее время существуют методы получения бездислокационных кристаллов. Измерение прочности таких кристаллов показывает, что она близка к теоретической.

Источники дислокаций

При деформации плотность дислокаций в кристаллах способна возрастать на несколько порядков (от 10² до 10¹² 1/см²). Для объяснения этого явления надо допустить, что внутри кристалла имеются некие источники дислокаций.

Механизм одного из таких источников был предложен Франком и Ридом (рис. 3.17).

 

Рис. 3.17. Источник дислокаций Франка−Рида [112]

 

Линия АВ представляет собой дислокацию с закрепленными концами (положение 0). Под действием внешнего механического напряжения дислокация начинает выгибаться в плоскости скольжения и занимает положение 1. Постепенное выгибание дислокации может происходить только при непрерывно возрастающем напряжении, которое достигает максимума, когда дислокация принимает форму полуокружности. При этом критическое напряжение

,

(3.20)

где L – длина отрезка АВ. При внешних механических напряжениях конфигурация становится нестабильной и дислокация расширяется самопроизвольно, последовательно занимая положения 2, 3, 4.

В положении 4 части дислокационной петли С и С^/ имеют винтовые компоненты противоположного знака, т. е. они движутся навстречу друг другу и взаимно уничтожаются. В результате происходит разделение дислокации на внешнюю и внутреннюю (5). Теоретически число дислокаций, возникающих от источника Франка−Рида, может быть бесконечным, но на практике это число увеличивается до тех пор, пока взаимодействие упругих полей дислокаций не сбалансирует критическое напряжение сдвига. После этого источник становится неактивным.

Бардин и Херинг предложили другой механизм генерации дислокаций, который отчасти аналогичен источнику Франка−Рида. В этом случае движение дислокации происходит за счет зарождения или поглощения вакансий, поэтому действие такого источника зависит от концентрации последних.

Кроме этих двух видов источников дислокаций, существуют и другие модели.

 

ИСПЫТАНИЕ СВОЙСТВ СТАЛИ

Цель работы: ознакомление с методами испытания свойств при определении марки стали.

Приборы и оборудование

- разрывная машина;

-образцы стержни, пластины;

-пресс Бринелля;

- маятниковый копр.