Priveşte la rădăcină

Cu ajutorul unei machete vom demonstra acest fenomen. Pentru efectuarea experimentului sunt necesare o serie de transformări a energiei, apoi comparăm valorile obţinute.

Este evident că nu toate mărimile fizice pot fi determinate prin măsurări directe. Uneori suntem nevoiţi să recurgem la măsurări indirecte, de aceea în cazul dat vom folosi resortul.

Factorii importanţi, care nu pot fi neglijaţi, constau în aceea că sistemul trebuie să fie echivalent în ambele variante, adică: nu ni se permite să schimbăm masa barei m_b (se are în vedere cantitatea de substanţă a barei), să mărim sau să micşorăm distanţa h (înălţimea la care se ridică greutatea – bara), iar arcul în poziţia iniţială nu trebuie să fie deformat.

Macheta reprezintă un sistem format de o greutate sub formă de bară având la o extremă un punct de sprijin cu posibilitatea de a se roti în plan vertical (fig. 3, fig. 5). Notăm poziţia iniţială a barei cu litera A, iar poziţia în care toată energia cinetică (Wc) a barei s-a transformat în energia potenţială a arcului (Wp) cu litera B. În poziţia A bara posedă o energie potenţială în comparaţie cu poziţia B.

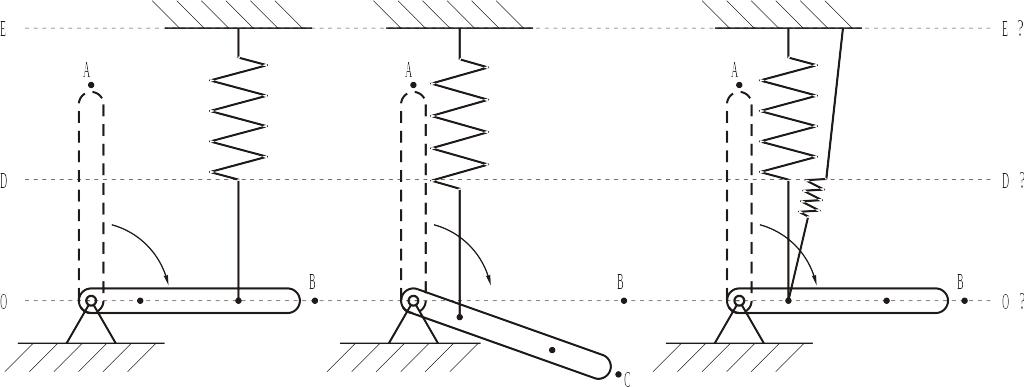
Fig. 3 Fig. 4 Fig. 5

Experimentăm prima variantă. Lăsăm să cadă bara din punctul A până în punctul B (fig. 3). La cădere Wp a barei se transformă în Wc, apoi Wc se transformă în Wp (deformarea arcului). Cu alte cuvinte energia potenţială şi cinetică a barei se cheltuieşte pentru deformarea resortului (fig. 3). Linia EE este paralelă cu linia DD şi paralelă cu linia OO (EE || DD || OO).

Efectuăm varianta a doua a experimentului. Aceeaşi bară cade din punctul A până în punctul B (fig. 4), dar schimbăm punctul de legătură cu bara, prin urmare Wc, se va cheltui pentru deformarea aceluiaşi arc. Se vede clar că bara a ajuns până în punctul C (fig. 4). Pentru claritate ne vom imagina că am redus cu mult viteza de cădere a barei, prin urmare observăm că bara aflându-se în punctul B (fig. 4) mai posedă o oarecare energie – _Wc. Datorită acestei energii _Wc bara se va deplasa din punctul B până în punctul C (fig. 4). Această energie cinetică Wc trebuie s-o transformăm în energie potenţială Wp cu condiţia să respectăm regulile prestabilite, şi anume: sistemul trebuie să fie echivalent în ambele variante, nu ni se permite să mărim distanţa BC (fig. 4). În acest caz vom utiliza un arc suplimentar cu o rigiditate (k₃) mai mică (fig. 5). Pentru a evita erorile repetăm experimentul, apoi comparăm rezultatele.

Notăm:

Wp – energia potenţială,

Wc – energia cinetică,

Wp₁ – energia potenţială pe care o posedă bara până la transformare, prima variantă,

Wp₂ – energia potenţială pe care o posedă bara până la transformare, varianta a doua,

Wp.t.₁ – energia potenţială după transformare, prima variantă (fig. 3),

Wp.t.₂ – energia potenţială după transformare, varianta a doua (fig. 5),

Wc – energia cinetică mică în comparaţie cu energia cinetică exercitată în sistem,

Wp – energia potenţială mică în comparaţie cu energia potenţială exercitată în sistem.

_x – pierderile de energie din sistem (fig. 3 şi fig. 5).

Legea conservării şi transformării energiei ne spune că: „energia nu se creează şi nici nu dispare, doar se transmite de la un corp la altul, ori se transformă dintr-o formă în altă formă în aceeaşi cantitate” [1, pag. 102]¹.

Notăm prin Wx - valoarea energiei cinetice [2, pag. 118, tab. 1]² a unui punct cercetat al corpului rotativ în sistemul dat (fig. 3 şi fig. 5).

, (1)

unde m_x , l_x , _x , h_x şi _x - sunt mărimi variabile ce corespund fiecărui punct cercetat în dependenţă de poziţia barei în sistem. Pentru fiecare sistem în parte (fig.3 şi fig.5) putem scrie următoarele relaţii:

(2)

(3)

Legea conservării energiei mecanice ne spune că: energia totală a sistemului conservator izolat e o mărime constantă (energia nu se creează şi nici nu dispare) [1, pag. 102]¹. Conform acestei legi avem:

(4)

(5)

La [1, pag. 102]¹, ultimul aliniat e scris că: „La rezolvarea problemelor în mecanică conform legii conservării şi transformării energiei se permite de a nu lua în consideraţie starea intermediară prin care trece sistemul, dar se va compara starea iniţială cu cea finală. De aceea la rezolvarea problemelor în mecanică trebuie de clarificat dacă se poate aplica legea conservării şi transformării energiei la problema dată – aceasta contribuie la o rezolvare simplă şi rapidă”.

Deoarece schimbarea energiei potenţiale a sistemului nu depinde de starea intermediară, putem scrie următoarele relaţii:

(6)

. (7)

Deoarece m₁ = m₂ , g – constant , h₁ = h_2, obţinem: sau (8)

Conform acestei legi, dacă: Wp₁ = Wp₂ , sau .

Atunci şi Wp.t.₁ = Wp.t.₂ sau ₁ = + _2. (9)

Deoarece k₁ = k₂ şi x₁ = x_2, atunci . (10)

În urma simplificări relaţiei 9 obţinem: ₁ = + _2, (11)

unde ₁ = ^′₁ + ^″₁ + ^′′′₁ şi ₂ = ^′₂ + ^′′₂ + ^′′′₂ + _{3 ,}

^′₁ şi ^′₂ - pierderile de energie în rulment,

^′′₁ , ^′′₂ şi ₃ - pierderile de energie la deformarea arcului,

^′′′₁ şi ^′′′₂ - pierderile de energie la înfruntarea aerului (diferenţa dintre valori este foarte mică, dar totuşi există).

După o analiză atentă, ştiinţifică, multilaterală, bazată pe valorile reale ale experimentului s-a constatat că:

^′₁ < ^′₂ deoarece F₁ < F₂ (vezi tabela 1, fig. 2, fig. 3 şi fig. 5)

^′′₁ < ^′′₂ + ₃ deoarece ^′′₁ = ^′′₂ (vezi relaţia 10)

^′′′₁ > ^′′′₂ deoarece ₁ > ₂ .

Deci obţinem: ₁ < ₂ sau ^′₁ + ^′′₁ + ^′′′₁ < ^′₂ + ^′′₂ + ^′′′₂ + ₃ (12)

unde ₂ - ₁ = _4. (13)

În urma simplificări relaţiei 11 obţinem: 0 = + _4. (14)

Deci avem: obţinem: Wp.t.₁  Wp.t.₂

În rezultat relaţia + _x nu se respectă, ceea ce vine în contradicţie cu legea conservării energiei mecanice, care spune că: „în cazul oricărei transformări de energie dintr-o formă în altă formă se păstrează egalitatea” sau se conservă [1, pag. 102]¹.

Conform acestei legi dacă Wp₁ = Wp₂, atunci şi Wp.t.₁ = Wp.t.₂, ceea ce, în cazul dat nu se respectă – Wp.t.₁  Wp.t._2. Fapt pe care l-am şi demonstrat pe cale experimentală. În acest caz, toţi fizicienii apelează la arma cea mai accesibilă (nu şi onorabilă) – negarea (?!). „O ştiinţă care nu se miră şi nu venerează e o ştiinţă moartă” (A. Einstein).

Consider că orice lege din fizică se poate aplica doar în domeniul dat şi în anumite limite, anumite condiţii, şi nici o lege nu poate fi absolută. Orice lege este limitată în dezvăluirea adevărului absolut. Cu alte cuvinte, o lege poate dezvălui un adevăr relativ. ADEVĂRUL ABSOLUT NU-L VOM CUNOAŞTE NICIODATĂ, CERCETĂRILE SUNT O CALE FĂRĂ SFÂRŞIT CE NE APROPIE DE EL.

Şi acest experiment ne demonstrează că energia nu se conservă, şi, prin urmare ENERGIA NU ESTE MATERIE. Energia este o MĂRIME FIZICĂ ce caracterizează un proces, un lucru.