10.Гидравлический расчёт трубопровода со сбросами и подкачками.

Разветвленным соединением называется совокупность нескольких простых трубопроводов, имеющих одно общее сечение – место разветвления (или смыкания) труб. Таким образом, трубопровод с отводом можно представить кАк последовательное соединение простого и разветвлённого трубопроводов (см. рис. 5.8).

Пусть основной трубопровод имеет трубопровод-отвод в точке B. Геометрические высоты z_С и z_D конечных сечений, а также и давления P_С и P_D в них могут быть различны.

Так же как и для параллельных трубопроводов, общий расход в основном трубопроводе до места разветвления Q будет равен сумме расходов на участках BD и BC: Q=Q_BC+q=(Q – q)+q.

Расчет сложных трубопроводов часто выполняют графоаналитическим способом, т.е. с применением кривых потребного напора и характеристик трубопроводов. Кривую потребного напора для сложного трубопровода следует строить следующим образом:

1) сложный трубопровод разбивают на ряд простых трубопроводов, для рис. 4.6 это трубопроводы AB, BC и BD;

2) строят кривые потребных напоров для каждого из простых трубопроводов AB, BC и BD (на рис. 5.8 обозначены тонкими линиями);

3) При расчете идут от конечных точек трубопровода к начальной точке, т.е. против течения жидкости:

а) складывают кривые потребных напоров для ветвей BD и BC по правилу сложения характеристик параллельных трубопроводов, на рис.5.8 полученная суммарная характеристика разветвлённого трубопровода обозначается основной линией BC(D);

б) полученную кривую BC(D) складывают с характеристикой последовательно присоединенного трубопровода AB по правилу сложения характеристик последовательно соединённых трубопроводов, суммарная характеристика сложного трубопровода на рис. 5.8 обозначается утолщённой линией ABC(D).

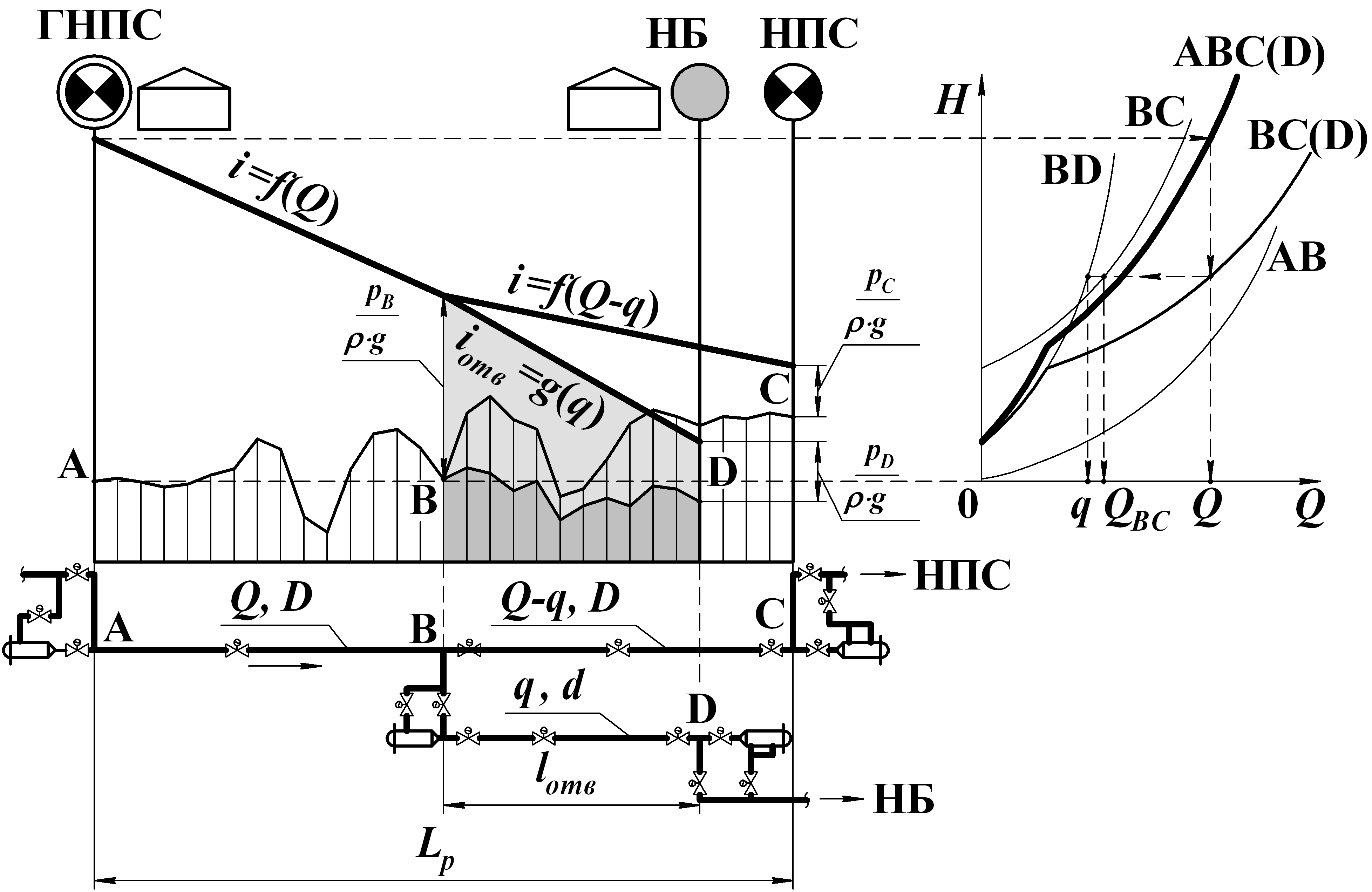
Рис. 5.8. Схема сложного трубопровода с отводом

Для численного решения запишем уравнение Бернулли для каждого из рассматриваемых простых трубопроводов протяженностью AB, BC и BD:

(5.34)

Таким образом, получаем систему трёх уравнений с тремя неизвестными: Q, q и p_B. Для решения системы уравнений (5.34) методом последовательного приближения можно использовать следующий алгоритм:

1. принимая q⁽⁰⁾=0 определяем Q⁽⁰⁾ сложив первое и второе;

2. из первого уравнения системы определяем давление ;

3. из третьего уравнения системы находим расход q⁽¹⁾;

4. сложив первое и второе уравнение системы с учётом того, что q= q⁽¹⁾, получим Q⁽¹⁾;

5. если выполняется условие (5.13), то система (5.34) решена с приемлемой точностью, в противном случае последовательно повторяя пункты (2), (3) и (4) находим , q⁽ⁱ⁾ и Q⁽ⁱ⁾ до тех пор пока не будет выполняться условие (5.13).

11.Характеристика линейной части. Режимы течения.

Характеристикой нефтепровода называется зависимость потерь напора от расхода. Для трубопровода постоянного диаметра можно записать

гдеNэ – число эксплуатационных участков.

Для определения гидравлического уклона воспользуемся следующей компактной формулой [18]

Где – гидравлический уклон при единичном расходе.

Тогда выражение можно переписать в виде

В общем случае, когда линейная часть нефтепровода оборудована лупингами и вставками, зависимость (1.28) примет вид

или учитывая, что

. (1.32)

С учетом (1.28) зависимость (1.32) принимает вид

. (1.33)

Начальная точка характеристики трубопровода совпадает с величиной отрезка z+N_Эh_ОСТ. В диапазоне расходов от 0 до Q_КР=DRe_КР/4 (область ламинарного режима течения при Re_КР=2320) зависимость H от Q линейная. При Q> Q_КР характеристика имеет вид параболы вида Q^2–m.

Величины , D и L_P определяют крутизну характеристики трубопровода. Чем меньше диаметр D и чем больше вязкость нефти  и расчетная длина нефтепровода L_Р, тем круче его характеристика.

При практических расчетах нет необходимости в построении характеристики H=f(Q) от начальной точки, то есть при Q=0. Вполне достаточно построить характеристику по нескольким точкам, соответствующим узкому интервалу расходов, ожидаемых при эксплуатации рассчитываемого нефтепровода.

Значения ,  и m зависят от режима течения жидкости и шероховатости внутренней поверхности трубы. Режим течения жидкости характеризуется безразмерным параметром Рейнольдса

где – относительная шероховатость трубы;

kЭ – эквивалентная (абсолютная) шероховатость стенки трубы, зависящая от материала и способа изготовления трубы, а также от ее состояния. Для нефтепроводов после нескольких лет эксплуатации можно принять kЭ=0,2 мм.