7.Гидравлический расчёт простого трубопровода.

При расчетах напорных трубопроводов основной задачей является либо определение пропускной способности (расхода), либо потери напора на том или ином участке, равно как и на всей трассе.

Простым называется нефтепровод постоянного диаметра, без ответвлений (постоянный расход по длине), течение жидкости в котором.

К сложным трубопроводам относятся системы труб с одним или несколькими ответвлениями, параллельными ветвями, вставками и т.д.

Чтобы определить величину энергии, которую необходимо сообщить жидкости, для того чтобы осуществить перекачку по данному трубопроводу с заданным расходом, пренебрегая разностью скоростных напоров, можно преобразовать к следующему виду

,

где z=(z_К–z_Н) – разность геодезических отметок, которая может быть как положительной (на подъём), так и отрицательной (под уклон).

Пьезометрическую высоту, стоящую в левой части уравнения, называют потребным напором Н_потр или, если эта пьезометрическая высота задана, то – располагаемым напором Н_расп, а её зависимость от расхода транспортируемой жидкости – гидравлической (Q–H) характеристикой трубопровода (см. рис. 5.2).

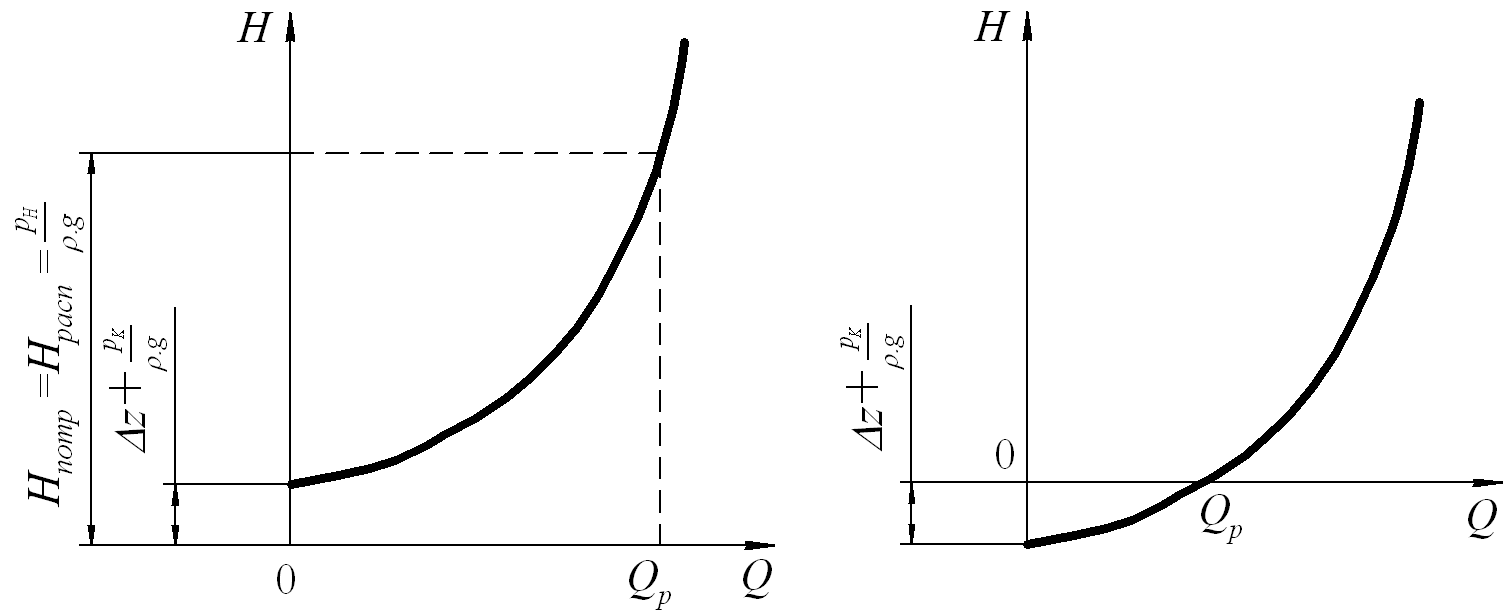
Пропускную способность участка МН, при известных давлениях p_Н и p_К можно определить одним из следующих методов:

1. Графо-аналитический метод, при этом строится кривая потребного напора и параллельно оси 0Q – прямая, отстоящая от начала координат на величину пьезометрического напора в начальном сечении. Пропускная способность определится абсциссой точки пересечения. Если нефть течёт под уклон и z> p_К/(g), а рельеф местности достаточно пологий, то точка пересечения кривой потребного напора с осью абсцисс определяет расход при движении жидкости самотеком.

2. Метод последовательных приближений хорошо зарекомендовал себя при решении трансцендентных уравнений. Решение находится при помощи такой последовательности приближений, которая сходится к корню уравнения и строится рекуррентно, т. е. каждое новое приближение вычисляют, исходя из предыдущего, при этом в качестве начального приближения в работе предложено λ=0,02.

Для реализации метода необходимо выразить расход, получим:

.

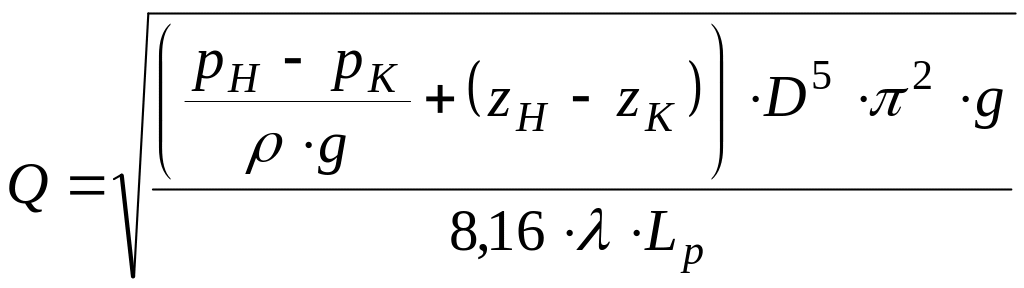Уравнение решается следующим образом: принимаем λ=0,02 и определяем расход в первом приближении Q⁽¹⁾, по значению которого определим режим течения и соответственно λ⁽¹⁾, после чего, подставив в правую часть λ⁽¹⁾, получим Q⁽²⁾. Последнее значение сравнивается со значением, полученным на предыдущей итерации. Если выполняется условие

, (5.13)

то расчёт заканчивают, если не выполняются то определяют λ⁽²⁾ и подставив в правую часть определяют Q⁽³⁾ после чего снова проверяют условие (5.13) и т.д.

3. Аналитическое решение для заданного гидравлического режима можно получить, подставив в уравнение (5.5) формулу (5.9) и выразив расход

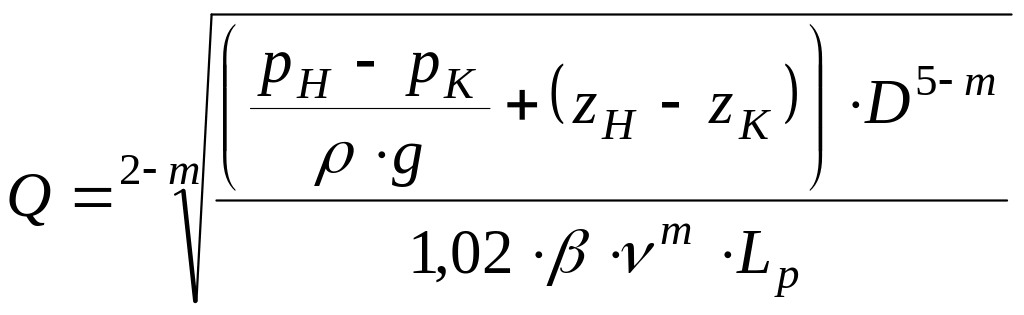. (5.14)

Если режим течения не известен, то для определения Q задаются значением коэффициентов  и m, а после проверяют соответствие принятого режима течения полученному расходу. Если полученный расход не соответствует принятому режиму, то принимают коэффициенты  и m для следующего режим течения, снова определяют Q и делают проверку.