Дифференциальные уравнения и ряды

Дифференциальным уравнением первого порядка называется любое уравнение вида

.

Решением дифференциального уравнения называется функция , подстановка которой в обращает уравнение в тождество:

.

Если уравнение можно разрешить относительно производной , то говорят, что уравнение записано в нормальной форме:

.

Задача Коши для уравнения заключается в нахождении решения , удовлетворяющего условию . Теорема о существовании и единственности решения задачи Коши утверждает, что, если функция и её частная производная непрерывны по совокупности аргументов, то найдется такой интервал , на котором имеется, и притом единственное, решение уравнения , для которого .

Общее решение дифференциального уравнения 1го порядка есть соотношение вида такое, что

1) для любого решения уравнения найдется константа , для которой ;

2) для любой константы неявное уравнение определяет некоторое решение дифференциального уравнения .

Имеется несколько стандартных уравнений первого порядка, в которых нахождение общего решения сводится к взятию подходящих интегралов.

Уравнения с разделяющимися переменными. Эти уравнения имеют вид

.

Решение уравнения сводится к преобразованию



Задача 4.3.а) Найти общее решение дифференциального уравнения

Решение. Запишем как и перегруппируем правую и левую части уравнения, так чтобы слева от знака равенства остались члены, зависящие только от , а справа –только от .

Вычисляя интеграл от левой части, получим:

.

Для правой части получаем

.

Окончательно,

.

Однородные уравнения. Уравнения имеют вид

.

Однородное уравнение сводится к уравнению с разделяющимися переменными с помощью замены

, ,

откуда следует, что

 .

Задача 4.3.б) Найти общее решение дифференциального уравнения

Решение. Правая часть уравнения является функцией от , поскольку . Будем искать решение в виде . Тогда , и исходное уравнение можно записать в следующем виде

 .

Разделяем переменные

 ,

откуда

Для первого слагаемого получаем:

.

Для второго,

.

Следовательно,

.

С учетом табличного интеграла

,

получаем

.

Остается вернуться к переменной .

Ответ: .

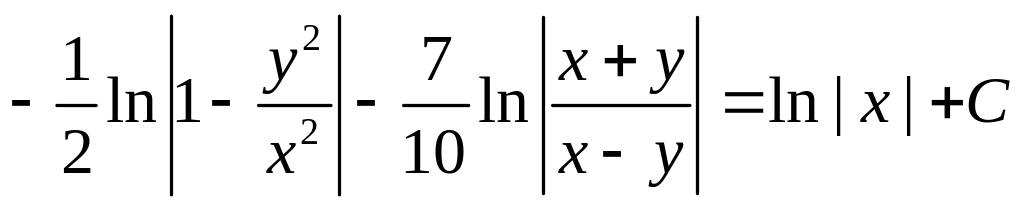Линейные уравнения. Линейные уравнения имеют вид

,

где и произвольные функции. Для решения линейных уравнений будем использовать метод Бернулли. Он заключается в том, что решение ищется в виде произведения двух функций , одну из которых мы выберем специальным образом. С учетом соотношения

,

получим

.

В качестве возьмем произвольное решение уравнения с разделяющимися переменными

.

Тогда , и функция есть решение уравнения

.

Задача 4.3.в Найти общее решение дифференциального уравнения

Решение. Положим , тогда и мы получаем

.

Выберем в качестве функции произвольное частное решение уравнения . Тогда уравнение эквивалентно системе двух уравнений

Первое уравнение представляет собой уравнение с разделяющимися переменными:

  ,

откуда

.

Поскольку нас интересует частное решение этого уравнения, положим . Тогда

 .

Второе уравнение системы теперь можно записать в виде

 ,

откуда

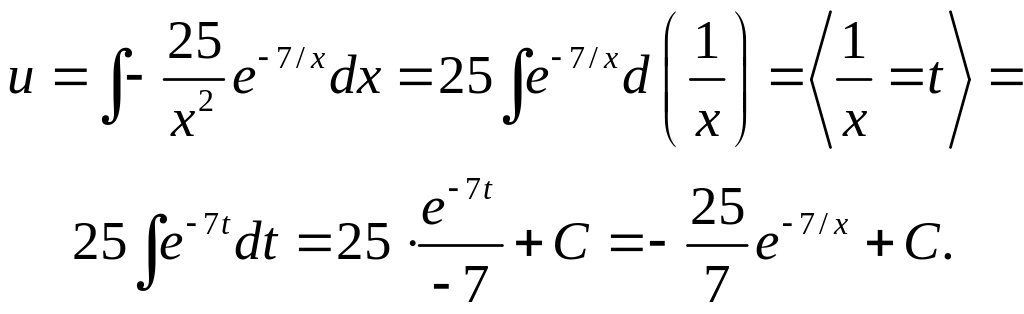
Ответ:

Уравнения Бернулли.

Уравнения Бернулли либо сводятся к линейным с помощью замены , либо интегрируются с помощью подстановки Бернулли .

Задача 4.3.г Найти общее решение дифференциального уравнения

Решение. Воспользуемся подстановкой Бернулли

, ,

откуда

Приравнивая нулю сумму второго и третьего слагаемых, получим систему

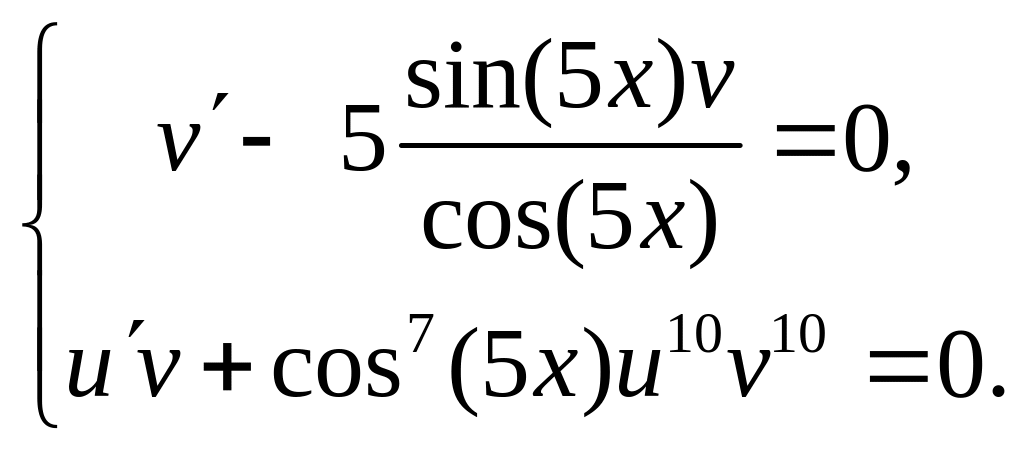
Находим частное решение первого уравнения



,

Следовательно,

.

Полагая , получим

.

Для второго уравнения системы теперь получаем

,

откуда

 .

Для интеграла слева получаем

.

Для интеграла справа получаем

.

Следовательно,

 .

Вовзращаясь к , получим

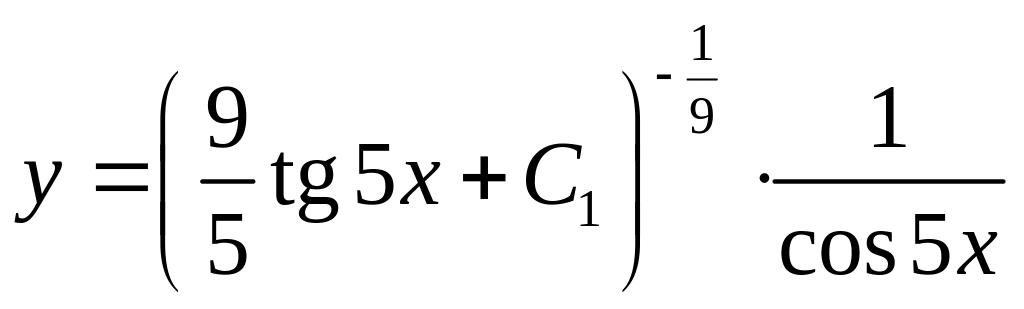
Дифференциальные уравнения второго порядка с постоянными коэффициентами и специальной правой частью.

Рассмотрим уравнение

где и константы, а функция в правой части уравнения имеет один из следующих трех видов

, , ,

 произвольный многочлен степени . Решение такого уравнения может быть получено следующим образом. Квадратное уравнение

назовем характеристическим уравнением для нашего уравнения. Пусть , – корни этого квадратного уравнения. Общее решение однородного уравнения

имеет вид

,

если ,  два различных вещественных числа; имеет вид

если и, наконец, решение имеет вид

если ,  комплексносопряженные корни характеристического уравнения.

Общее решение неоднородного уравнения может быть получено как сумма общего решения однородного уравнения и произвольного частного решения неоднородного уравнения . Это частное решение можно найти методом неопределенных коэффициентов по следующему правилу.

Сопоставим функции в правой части исходного уравнения число . Если не является корнем характеристического уравнения, то частное решение ищем в том же виде, в каком записана правая часть, то есть

если , и в виде

если или . Здесь , многочлены степени , коэффициенты которых можно определить, подставив в исходное уравнение и приравняв коэффициенты при одинаковых функциях. Если является корнем характеристического уравнения (эта ситуация называется резонансом), то степень многочленов , увеличивается на 1.

Задача 4.4.а. Найти решение задачи Коши для дифференциального уравнения.

Решение. Сначала найдем общее решение однородного уравнения. Выпишем характеристическое уравнение



Следовательно, общее решение линейного однородного уравнения имеет вид

.

Поскольку корни характеристического уравнения не совпадают с соответствующим показателем правой части , частное решение неоднородного уравнения будем искать в виде

.

Получаем:

,

.

Подставляя , , в исходное уравнение, получаем:

Сокращая на и приводя подобные, получим

,

,

откуда



Общее решение неоднородного уравнения имеет, следовательно, вид

.

Теперь найдем решение задачи Коши. Имеем:

,

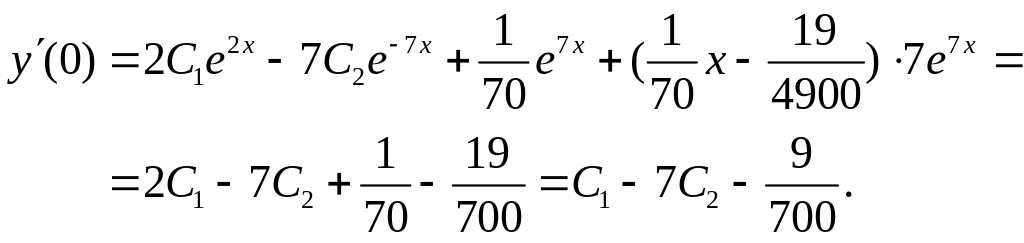
Поскольку , второе уравнение имеет вид . Решаем систему линейных уравнений на неизвестные и :

Умножая первое уравнение системы на 2 и вычитая из него второе уравнение, получим:

 .

Далее,

.

Ответ: .

Задача 4.4.б. Найти решение задачи Коши для дифференциального уравнения.

Решение. Характеристическое уравнение имеет вид:

,

откуда

,

где  мнимая единица. Следовательно, , , и общее решение однородного уравнения есть

.

Правая часть исходного неоднородного уравнения имеет то же собственное число, что и характеристическое уравнение, следовательно, мы имеем дело с резонансом. Поэтому частное решение неоднородного уравнения следует искать в виде

.

Подставляя в исходное уравнение, с учетом того, что

,

получим:

откуда

и, следовательно,

, .

Таким образом, частным решением неоднородного уравнения является функция

.

Общее решение неоднородного уравнения может быть записано в виде

.

Найдем константы и , при которых выполнены краевые условия

, .

Так как

,

получаем систему линейных уравнений на и :

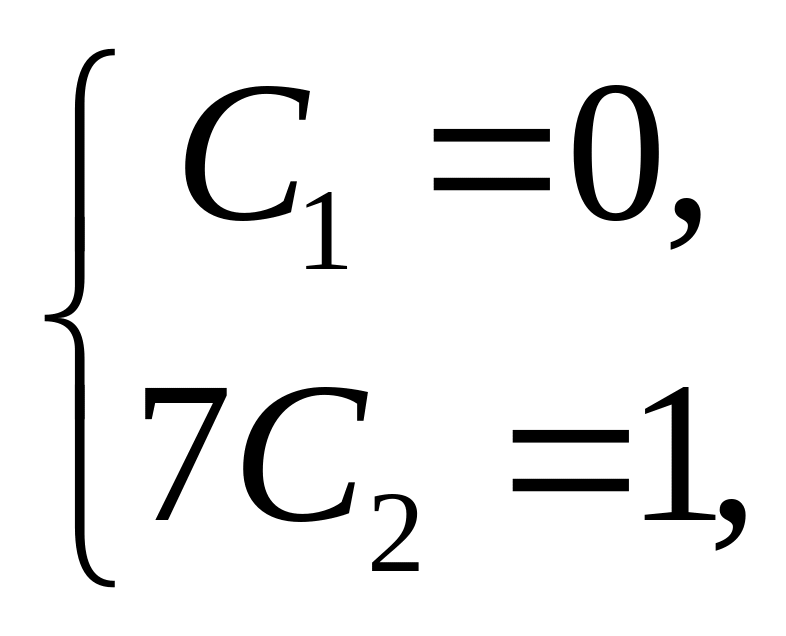
откуда .

Числовые и функциональные ряды.

Числовым рядом называется формальное выражение вида

,

где число слагаемых неограниченно. Выражение называется общим, или ным, членом ряда. Сумме бесконечного числа слагаемых нужно придать смысл. Делается это следующим образом. Назовем –ной частичной суммой ряда сумму первых слагаемых

.

Суммой ряда называется предел частичных сумм

.

Ряд с конечной суммой называется сходящимся. Если предела частичных сумм не существует, говорят, что ряд расходится.

Найти сумму ряда точно почти никогда не удается. В действительности важно знать, сходится ли ряд вообще, или нет. Именно этот вопрос нас и будет интересовать.

Необходимое условие сходимости ряда

.

Ряд называется знакоопределенным, если все слагаемые имеют один знак. Имеется несколько простых достаточных условий сходимости знакоположительных рядов.

Признак Даламбера. Пусть существует предел

.

Тогда, если , то ряд сходится; если , то ряд расходится.

Признак Коши (радикальный). Пусть существует предел

.

Если , то ряд сходится, если , то ряд расходится.

Признак Коши (интегральный). Если найдется такая монотонно убывающая положительная функция , что для всех , то тогда из сходимости интеграла следует сходимость ряда , а из расходимости интеграла следует расходимость ряда .

Иногда для исследования сходимости знакоположительного ряда удобно использовать признаки сравнения. Если и ряд сходится, то и сходится. Если и ряд расходится, то и расходится.

Из признаков сходимости знаконеопределенных рядов нам потребуется признак Лейбница сходимости знакочередующегося ряда. Если мы имеем ряд

,

где , и при этом , то ряд сходится. Для рядов, удовлетворяющих условию Лейбница (то есть знакочередущихся рядов, у которых монотонный предел модуля –го члена равен нулю), имеется следующая полезная оценка:

,

то есть остаток ряда, начиная с произвольного члена , по модулю не превосходит этого члена.

Задача 4.5.а Исследовать сходимость ряда

Решение. Имеем , , и, по признаку Даламбера,

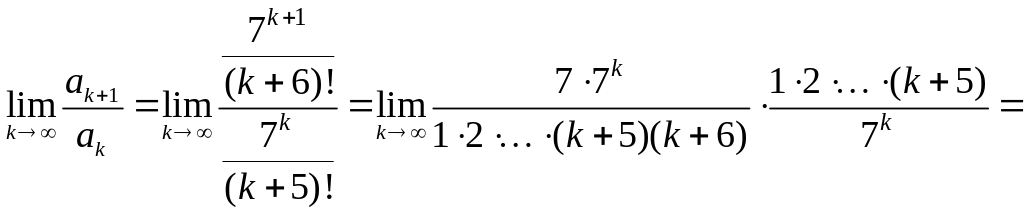
Следовательно, ряд сходится.

Задача 4.5.б Исследовать сходимость ряда .

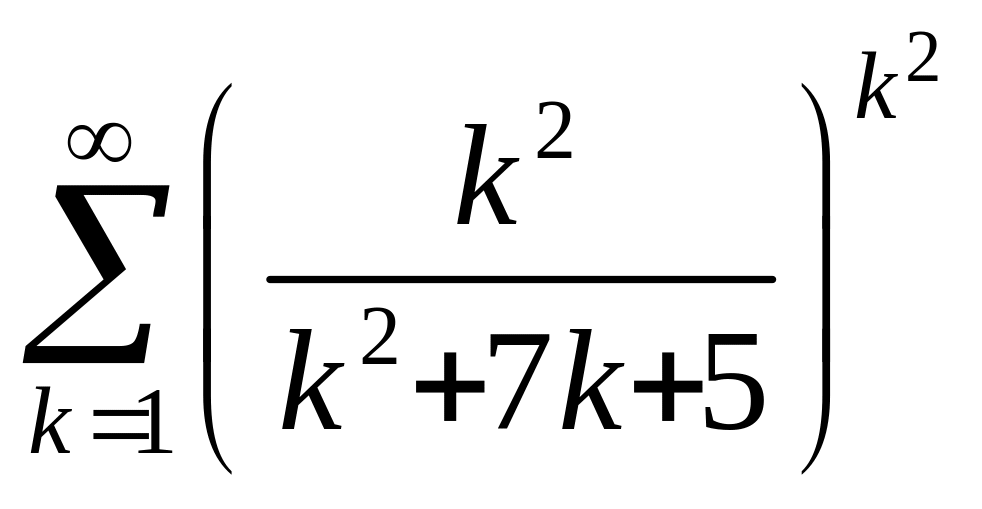Решение. Имеем: 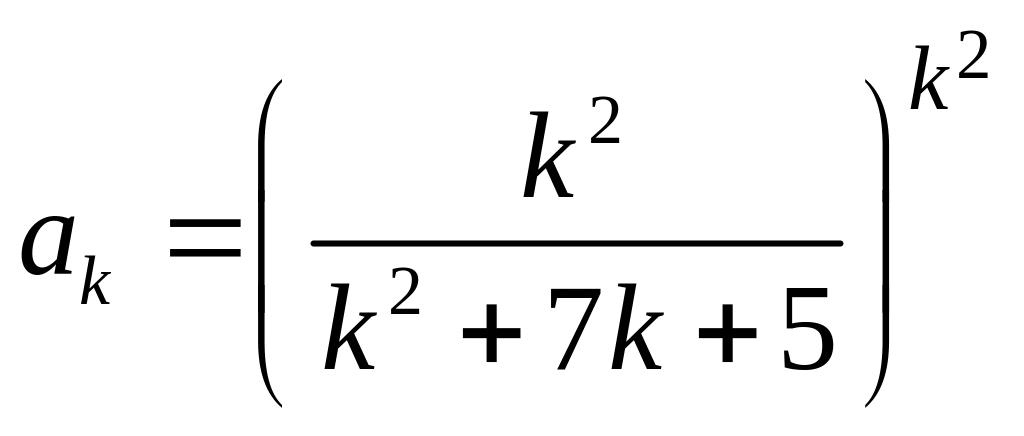, и, по радикальному признаку Коши,

Следовательно, ряд сходится.

Задача 4.5.в Исследовать сходимость ряда

Решение. Имеем:

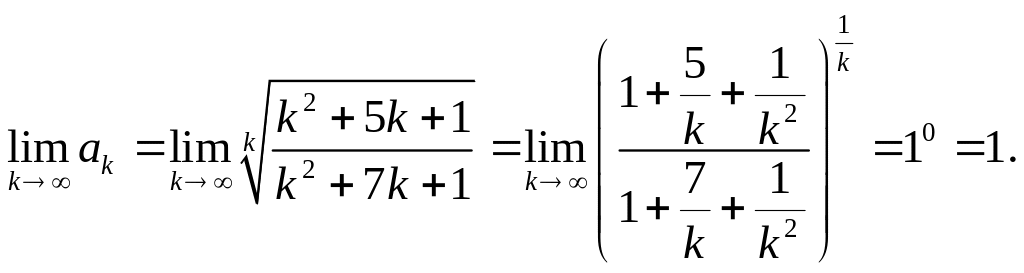
Следовательно, не выполнено необходимое условие сходимости ряда и ряд расходится.

Задача 4.5.г Исследовать сходимость ряда .

Решение. Подберем ряд для сравнения. С учетом неравенств , , выполненных при всех , имеем

.

Для ряда воспользуемся интегральным признаком Коши. Положим . Тогда

.

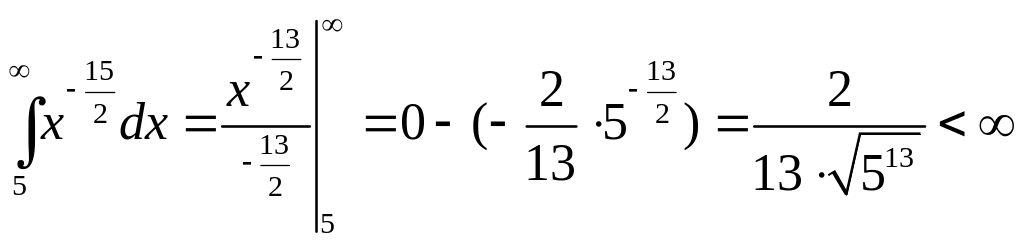Следовательно, и ряд , и ряд сходятся.

Функциональным рядом называется выражение вида

Для каждого фиксированного значения параметра сходимость ряда определяется как предел частичных сумм соответствующего числового ряда. Область сходимости – множество значений , при которых ряд сходится. Для степенного ряда

областью сходимости является интервал , где . Здесь обозначает верхний предел последовательности , то есть наибольший из пределов всех сходящихся подпоследовательностей . Внутри данного интервала ряд сходится абсолютно (то есть сходится ряд, составленный из модулей членов). Сходимость степенного ряда в граничных точках исследуется отдельно.

Рядом Тейлора функции в точке называется степенной ряд

где

.

Если значение равно сумме ее ряда Тейлора , то функция называется аналитической в точке . Ряд Тейлора определен однозначно в том смысле что, если для какого-либо степенного ряда, то тогда . Степенные ряды внутри области сходимости можно почленно дифференцировать и интегрировать: если , то тогда

,

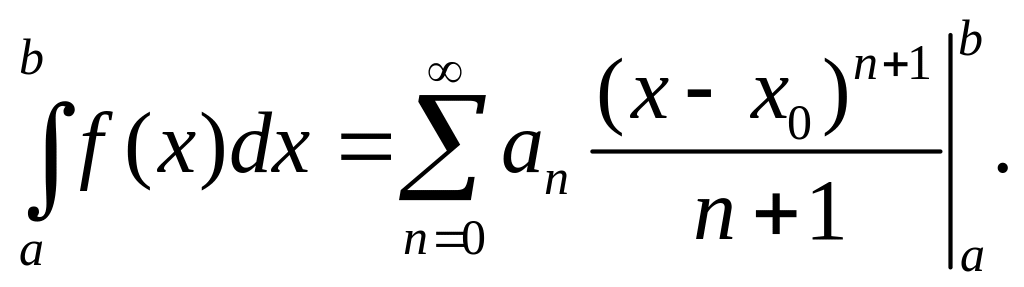
Задача 4.6. Выписать ряд Тейлора функции с центром в точке . Найти область сходимости ряда.

Решение. Воспользуемся формулой суммы бесконечной геометрической прогрессии:

при .

Для этого сначала поделим с остатком числитель дроби на знаменатель:

.

Далее,

где .

Следовательно,

.

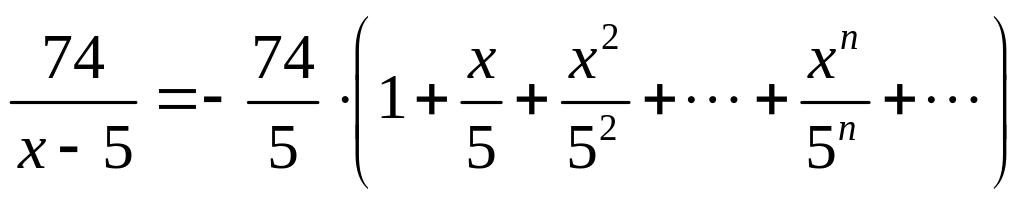Окончательно,

Чтобы найти область сходимости ряда, воспользуемся признаком Даламбера. Зафиксируем и рассмотрим ряд из модулей:

Тогда общий член ряда записывается формулой , , и, следовательно,

Согласно признаку Даламбера при ряд сходится, а при ряд расходится. Интервал сходимости ряда . Исследуем поведение ряда в граничных точках . При получаем:

.

Поскольку , то необходимое условие сходимости ряда оказывается невыполненным, и ряд расходится. При ряд расходится по той же причине.

Задача 4.7. Вычислить приближенно с точностью до =0.001 значение интеграла , используя разложение подынтегральной функции в ряд Тейлора.

Решение. Воспользуемся формулой

Подставляя вместо , получим:

.

Интегрируя почленно, получим

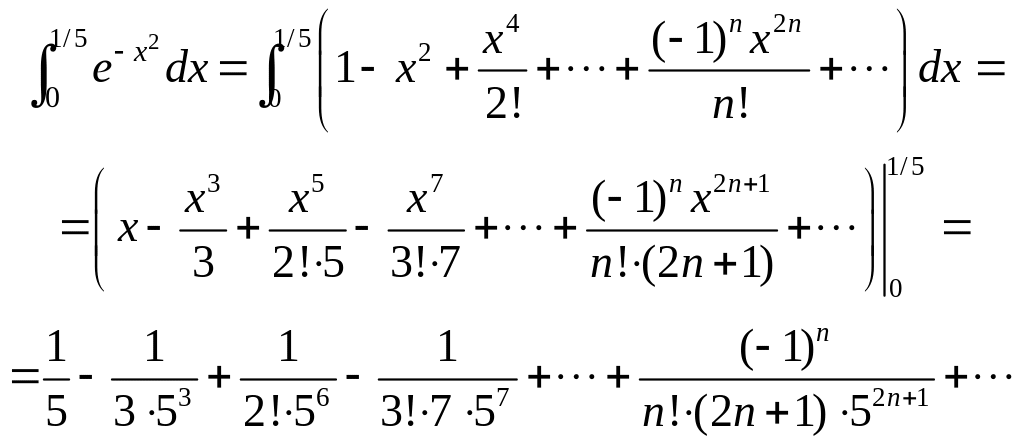
Чтобы понять, сколько членов ряда нужно взять, чтобы найти сумму ряда с точностью до 0.001, воспользуемся оценкой остатка лейбницевского ряда: сумма отброшенных слагаемых по модулю не превосходит первого отброшенного числа. Таким образом, остается решить, для какого натурального числа впервые будет выполнено неравенство

.

Последовательно подставляя в данное неравенство значения , убеждаемся, что впервые неравенство оказывается выполненным при :

.

В частности, все слагаемые ряда, начиная с , можно отбросить.

Ответ: .

Рядом Фурье на интервале называется функциональный ряд вида

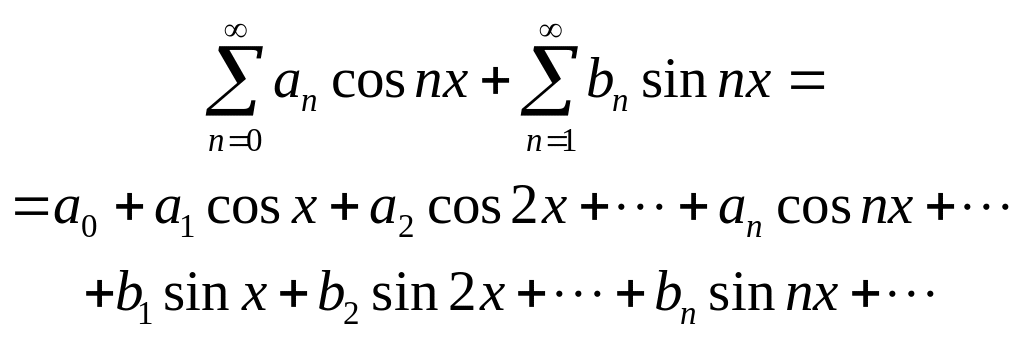
Если функция непрерывна (или имеет конечное число разрывов первого рода) на интервале , и ее производная существует всюду, кроме конечного числа точек, и при этом ограничена по модулю , то значение в точках непрерывности равно сумме ряда Фурье

,

коэффициенты и которого определяются по формулам

, , , ,.

Задача 4.8. Представить функцию рядом Фурье в интервале (0,2).

Решение. Имеем:

.

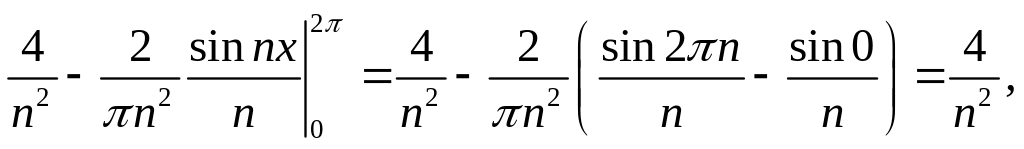
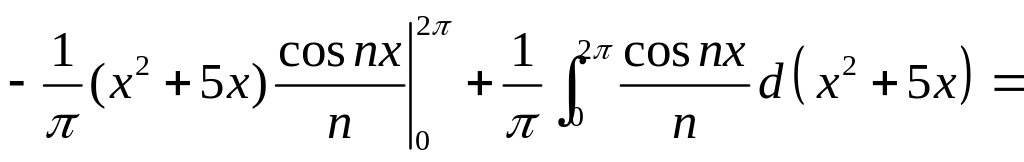
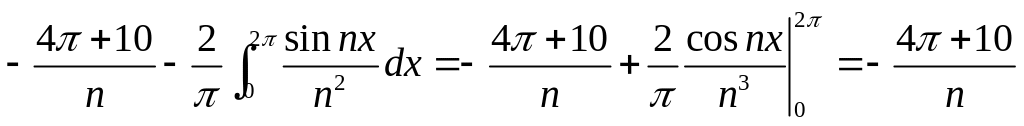Окончательно, получаем:

.