3. Функции нескольких переменных.

Частной производной функции по переменной в точке называется предел

.

Аналогично определяются частные производные по и по . При дифференцировании по одной переменной все остальные считаются постоянными.

Например, если , то

, , .

Градиентом функции называется вектор

Производной функции по направлению вектора , где , называется число

.

Теорема о полном дифференциале гласит, что

.

Поэтому

.

Если , то для взятия производной по направлению нужно предварительно нормировать вектор , поделив его на длину .

Касательная к кривой, заданной неявным уравнением , в точке определяется уравнением

** .

Нормаль к той же кривой определяется уравнением

.

Задача 3.1. Найти градиент функции в точке (1,5).

Решение. Имеем:

Подставляя 1 вместо и 5 вместо , получим

.

Аналогично,

откуда . Окончательно,

.

Задача 3.2. Вычислить производную функции по направлению вектора в точке (1,1).

Решение. Длина вектора равна , поэтому перейдем к вектору , имеющему то же направление, что и вектор , но единичную длину. Далее,

, .

В точке имеем . По определению производной по направлению получаем:

.

Задача 3.3. Найти производные функции .

Решение. Имеем:

,

.

По определению вторых частных производных, имеем:

Задача 3.4. Для кривой, задаваемой уравнением , написать уравнения касательной и нормали в точке (1,1).

Решение. Подставим в уравнение касательной и нормали значения частных производных функции в точке .

, .

Уравнение касательной имеет вид:

 .

Уравнение нормали имеет вид

 .

4. Интегральное исчисление. Неопределенные интегралы.

Операция интегрирования является обратной к операции дифференцирования.

Определение 1. Функция называется первообразной для функции , если .

У функции имеется бесконечное множество первообразных, при этом все они отличаются друг от друга на константу: если и - две первообразные для функции , то , где С=const.

Определение 2. Множество всех первообразных для функции называется неопределенным интегралом от и обозначается символом .

Если  любая первообразная для , то , где С = const.

Основные свойства неопределенного интеграла.

1. (в частности, ).

2. .

3. .

Необходимо знать интегралы основных элементарных функций (табличные интегралы):

( )

Для нахождения интегралов используются следующие методы.

1) Преобразование подынтегрального выражения, при помощи которого интеграл преобразуется к одному или нескольким табличным интегралам.

2) Подведение под знак дифференциала, основанное на формуле .

,

где .

3) Замена переменной. Если , то

.

4) Интегрирование по частям:

.

5) Интегрирование рациональных дробей вида (где ,  многочлены) основано на представлении дроби в виде суммы многочлена и простейших рациональных дробей вида

.

Разложение рациональных дробей в сумму простых дробей осуществляется с помощью метода неопределенных коэффициентов, который будет продемонстрирован ниже, на частном примере.

Имеют место формулы

,

( ).

Интеграл можно найти, выделяя полный квадрат в знаменателе: , с последующей заменой .

Интеграл сводится к интегралу следующего вида:

.

6) Функции, содержащие иррациональности, интегрируются в том случае, когда интеграл от них сводится к интегралу от рациональной дроби с помощью какойлибо замены переменной. Приведем несколько примеров интегрируемых иррациональных функций.

) Интегралы вида

где  рациональная функция, а , ,  натуральные числа. Метод интегрирования  замена , где  наименьшее общее кратное чисел , , .

) Интегралы вида сводятся к табличным при помощи замены .

) Интегралы , где , и  рациональные числа. Интегралы такого вида сводятся к элементарным только при следующих соотношениях параметров , и .

Если целое, то следует использовать замену , где  наименьшее общее кратное знаменателей дробей , .

Пусть теперь  наименьшее общее кратное знаменателей дробей , . Если  целое, то интеграл сводится к интегралу от рациональной функции с помощью замены .

Если целое, то интегрирование осуществляется при помощи замены .

) Подстановки Эйлера. Они применяются к интегралам вида , где рациональная функция. Имеется три вида подстановок Эйлера.

;

;

,

где , корни многочлена .

Тригонометрические замены. Для интегралов используется замена . Для интегралов используется замена . Для интегралов используется замена . В каждом из трех случаев получается интеграл от рациональной функции, зависящей от и .

7) Интегрирование выражений вида , где – рациональная функция от . В разных случаях используются замены , , , . Если ни одна из этих замен не позволяет получить интеграл от рациональной функции, то используется универсальная тригонометрическая подстановка . Тогда , , , и подынтегральное выражение сведется к рациональной дроби.

В задачах 4.1.а4.1.ж. требуется вычислить неопределенные интегралы.

Задача 4.1.а. .

Решение. .

Задача 4.1.б. .

Решение.

1)

2) .

Ответ: .

Задача 4.1.в. .

Решение. = = = = = = = = = .

Задача 4.1.г. .

Решение. Интегрируем по частям: = .

Интегралы вида находятся с помощью подстановки .

Задача 4.1.д. .

Решение. = = = = = = = .

Задача 4.1.е. .

Решение. Разложим подынтегральную функцию в сумму простых дробей. Воспользуемся методом неопределенных коэффициентов.

,

,

,

откуда

 

Следовательно,

1) ;

2)

= .

Ответ: .

Интегралы вида для нечетного можно находить при помощи подстановки .

Задача 4.1.е. .

Решение. .

Разложим подынтегральное выражение в сумму простых дробей:

,

,

Приравнивая коэффициенты при одинаковых степенях в левой и правой частях тождества, получим систему четырех уравнений с четырьмя неизвестными A, B, C, D:

 

откуда

Окончательно, получим . Следовательно, разложение дроби в сумму простейших имеет вид:

.

В результате, получаем

= = = .

Задача 4.1.ж. .

Решение. Используем универсальную тригонометрическую подстановку.

= = = = = .

Определенные интегралы. Площади плоских фигур.

Определенный интеграл (Римана) позволяет распространить формулу площади прямоугольника на площадь более или менее произвольной плоской геометрической фигуры. В основе понятия определенного интеграла лежит так называемая интегральная сумма, определяемая следующим образом. Пусть задана функция , определенная на отрезке . Разобъем отрезок произвольным образом на частей , , ( , ). В частности, можно разбить на равных частей, тогда длина каждого отрезка разбиения будет равна . В общем случае, пусть

.

Возьмем, опять же произвольным образом, внутри каждого из отрезков по точке . Интегральной суммой функции на по разбиению называется число

Если , то интегральная сумма есть площадь фигуры, состоящей из прямоугольников со сторонами и , . Интуитивно ясно, что, чем меньше максимальная длина отрезков разбиения , тем точнее эта фигура из прямоугольников приближает криволинейную трапецию с основаниями , и “боковыми сторонами” , . Интеграл от функции по отрезку есть предел по всевозможным разбиениям , когда .

Предел понимается здесь в обычном смысле: число называется определенным интегралом от по (обозначается как ), если для произвольного найдется такое , что, как только разбиение отрезка удовлетворяет условию , интегральная сумма , отвечающая этому разбиению, будет отличаться от не больше, чем на : .

Геометрический смысл определенного интеграла.

Значение (с точностью до знака) есть площадь криволинейной трапеции, заключенной между графиком функции , осью абсцисс и прямыми , . В частности, если на отрезке заданы две функции и , причем , то площадь криволинейной трапеции, заключенной между графиками этих двух функций, равна .

Связь между определенным и неопределенным интегралом заключена в формуле НьютонаЛейбница:

,

или, в другой записи, , где  произвольная первообразная функции .

Справедливы следующие две формулы – замена переменной интегрирования и интегрирование по частям.

Замена переменной.

Пусть  произвольная непрерывно дифференцируемая функция, определенная на некотором отрезке , причем , , и при любом . Тогда

Интегрирование по частям.

.

Задача 4.2.а. Найти площадь фигуры, ограниченной линиями , .

Решение. Заметим, что первое уравнение является уравнением параболы, ветви которой направлены вправо. Второе уравнение определяет прямую линию.

Найдем пересечения графиков функций и сделаем рисунок. Для этого решим систему



откуда , что дает и .

3

0

Из рисунка видно, что фигура состоит из двух частей. При получаем сегмент параболы . При криволинейная трапеция заключена между прямой и параболой . Следовательно, площадь фигуры равна сумме двух следующих двух интегралов:

Для первого интеграла получаем:

Для второго интеграла получаем:

Таким образом, . Ответ: .

Задача 4.2.б. Найти площадь фигуры, ограниченной линиями , , .

Решение. На отрезке выполняется неравенство . Поэтому найдем площадь, используя формулу .

= .
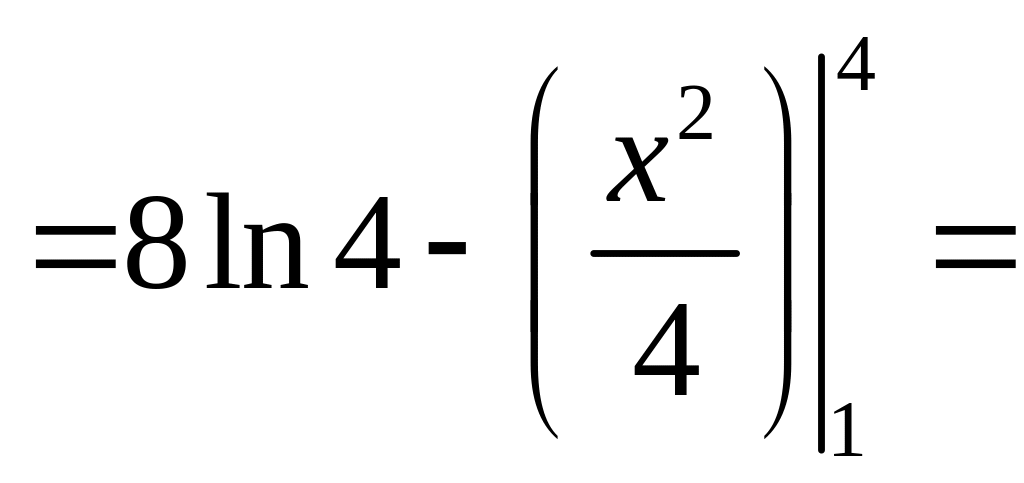