3.3 Приклад синтезу автономної баср

3.3.1 Умова задачі

Задана двозв’язна БАСР (рис. 3.3).

Рис. 3.3 Матрична структурна схема двозв’язної АСР

Відомі динамічні характеристики (передаточні функції) двозв’язного об’єкта регулювання, який представлений двома матричними ланками:

W_о – передаточна матриця прямих сепаратних каналів об’єкта

, (3.4)

L – передаточна матриця зворотних перехресних зв’язків об’єкта

. (3.5)

Також відомі передаточні функції сепаратних регуляторів

R' – передаточна матриця сепаратних регуляторів

(3.6)

Необхідно забезпечити автономність БАСР відносно задаючих дій, для чого треба ввести штучні (компенсуючі) перехресні зв’язки між сепаратними регуляторами і визначити їх передаточні функції.

3.3.2 Рішення задачі

Спочатку розв’яжемо задачу I методом (класичним), використовуючи алгоритм, описаний вище (див. 3.2):

1. Вводять штучні перехресні зв’язки за II типовим варіантом (рис. 3.1). Матрична структурна схема розробленої системи зв’язаного регулювання представлена на рис. 3.4.

R'

К

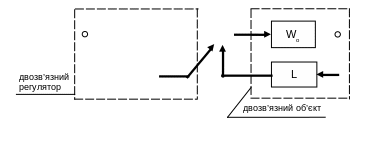
Рис. 3.4 Матрична структурна схема системи зв’язаного регулювання

К – передаточна матриця штучних перехресних зв’язків

, (3.7)

члени якої (К₁₂, К₂₁) – це передаточні функції штучних перехресних зв’язків. Їх треба визначити із умови забезпечення автономності відносно задаючих дій .

2. Виконують еквівалентні перетворення структурної схеми розробленої системи зв’язаного регулювання (рис. 3.4) до типової структурної схеми, зображеної на рис 3.2.

Неважко помітити, що передаточні матриці А та В дорівнюють одиничній матриці Е, тобто

. (3.8)

Визначають приведені передаточні матриці двозв’язного об’єкта Н та двозв’язного регулятора R

, (3.9)

. (3.10)

Для визначення Н за формулою (3.9) виконують послідовно відповідні операції з матрицями

, (3.11)

, (3.12)

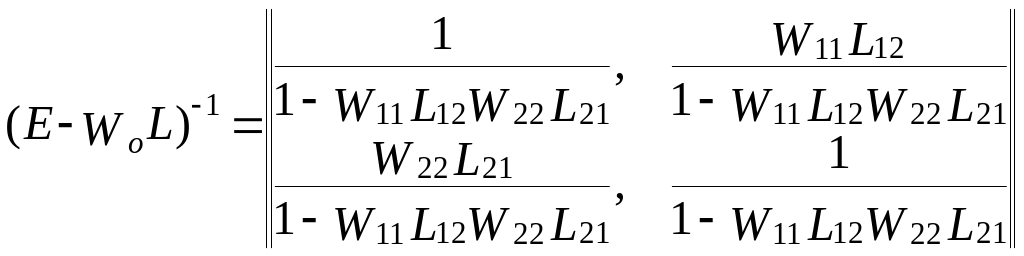, (3.13)

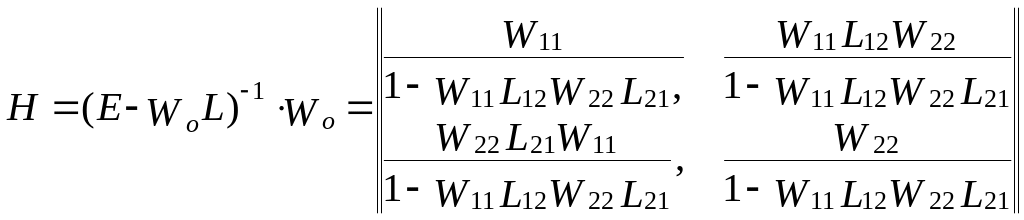. (3.14)

Приведену передаточну матрицю двозв’язного регулятора R визначають за формулою (3.10)

. (3.15)

3. Так як за умовою задачі виконується синтез БАСР, автономної відносно задаючих дій , то на передаточну матрицю замкнутої БАСР за каналом задаючих дій G_S накладають умову діагональності, тобто вважають, що вона діагональна

, (3.16)

де G₁₁ , G₂₂ – відповідно передаточні функції замкнутих автономних сепаратних систем регулювання.

4. Виконують відповідні операції з матрицями у правій частині матричного рівняння (3.2)

, (3.17)

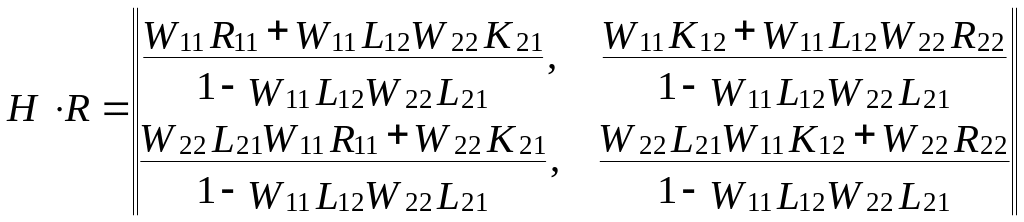(3.18)

(3.19)

Прирівнюючи відповідні члени матриць (3.16) і (3.19), отримують таку систему алгебраїчних рівнянь

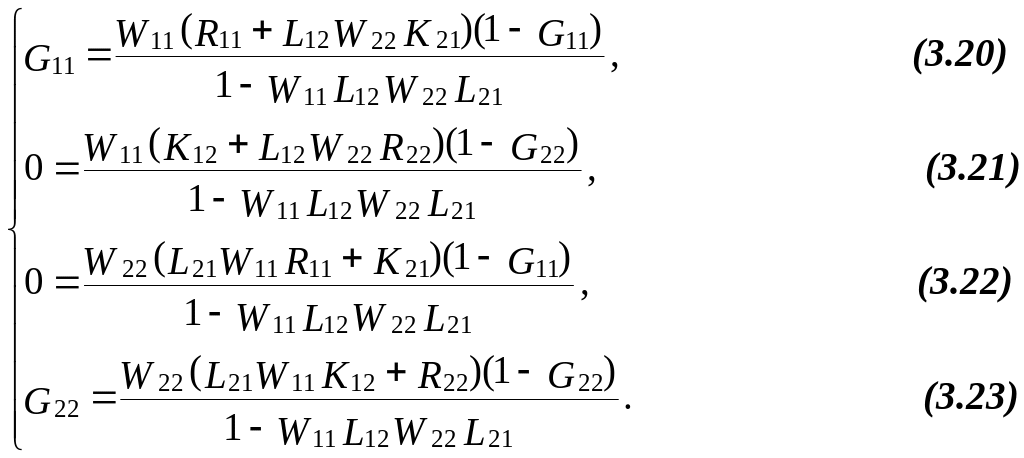
Розв’язують дану систему рівнянь у такій послідовності:

• Із рівняння (3.21), враховуючи що передаточні функції W₁₁ та 1–G₁₁ не дорівнюють нулю, випливає

звідки

.

Подібно із рівняння (3.22) визначають К₂₁

.

• Після підставки знайдених передаточних функцій штучних перехресних зв’язків К₂₁ та К₁₂ в рівняння (3.20) і (3.23), із них визначають передаточні функції замкнутих автономних сепаратних систем

.

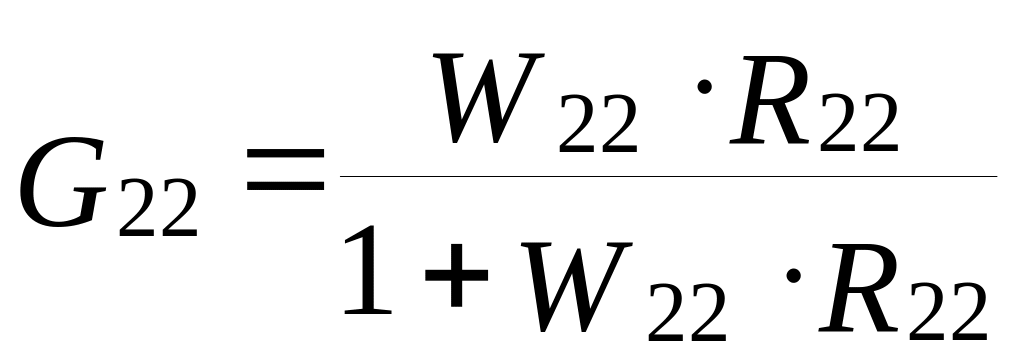А тепер розв’яжемо цю ж задачу II методом. Для того, щоб прослідкувати хід сигналів і скласти рівняння їх балансу розроблену систему зв’язаного регулювання (див. рис. 3.4) представляють у вигляді розгорнутої структурної схеми (рис. 3.5).

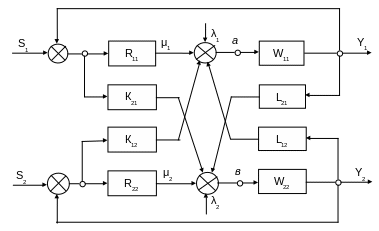
Рис. 3.5 Розгорнута структурна схема системи зв’язаного регулювання

Припустимо, що у другій сепаратній системі регулювання змінилося завдання, тобто

S₂ ≠ 0, а S₁ = λ₁ = λ₂ =0. (3.24)

Вибирають точку "а" на вході об’єкта першої сепаратної системи. Умовно розривають основний зворотній зв’язок в першій сепаратній системі. Складають рівняння балансу сигналів відносно точки "а"

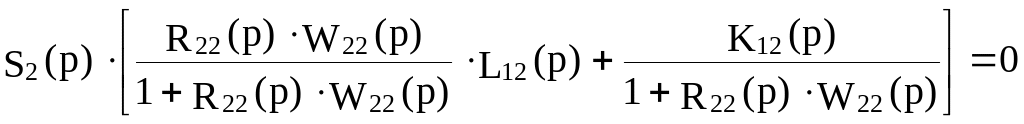. (3.25)

Рівняння (3.25) – це умова автономності, тобто незалежності Y₁ від S₂. Із рівняння (3.25) знаходять

.

Передаточну функцію компенсатора К₂₁(р) знаходять подібно із умови автономності, незалежності Y₂ від S₁, склавши рівняння балансу сигналів відносно точки "в"

. (3.26)

Із рівняння (3.26) знаходять

.