2.3 Приклад синтезу комбінованої аср

2.3.1 Умова задачі

Динамічні характеристики комбінованої АСР (рис. 2.1 а) за каналами збурення та регулювання описуються відповідними передаточними функціями

; (2.11)

(2.12)

В якості регулятора замкнутої системи застосовується П-регулятор з передаточною функцією

R(р) = – S. (2.13)

Необхідно розрахувати настройки регулятора, тобто S_опт, вибрати компенсатор ­– визначити передаточну функцію

R_k(р)

і знайти його параметри (коефіцієнти передаточної функції) із умови інваріантності на нульовій та робочій частотах.

2.3.2 Рішення задачі

Етап I. Визначають настройки регулятора і робочу частоту замкнутої системи методом Циглера-Нікольса (дивись 2.2).

Із передаточних функцій (2.12, 2.13) отримують АФХ об’єкта та регулятора

; (2.14)

. (2.15)

Визначають амплітудно-частотні та фазочастотні характеристики об’єкта та регулятора

;

;

;

.

Умова знаходження замкнутої АСР на границі стійкості, система рівнянь (2.2), після підстановки відповідних характеристик буде виглядати так

(2.16)

Розв’язуючи систему рівнянь (2.16) визначають критичну частоту ω_кр і критичний коефіцієнт підсилення регулятора S_кр

ω_кр = 1,517; S_кр = 1,211.

Робочу частоту ω_р приймають приблизно рівною ω_кр , а оптимальну настройку регулятора рівною S_опт = 0,5 · S_кр = 0,606.

Етап II. Визначають передаточну функцію "ідеального" компенсатора із умови інваріантності (2.6)

;

. (2.17)

Перевіряють умови (2.9, 2.10) можливості фізичної реалізації "ідеального" компенсатора

τ_уλ = 1,52 > τ_уμ = 1,42;

m = 1 = n = 1.

Так як умови (2.9, 2.10) виконуються, то "ідеальний" компенсатор може бути фізично реалізованим. Але технічна реалізація пристрою з передаточною функцією (2.17) достатньо складна, так як він за структурою представляє собою послідовне з’єднання ланки чистого запізнювання, реальної диференцюючої ланки та аперіодичної ланки I-го порядку. Тому треба підібрати реальний компенсатор більш простої структури.

Етап III. Вибирають реальний компенсатор.

Для вибору типу реального компенсатора будують частотні характеристики ідеального компенсатора у діапазоні частот [0, ω_р]. Із рівняння (2.17) при р = іω отримують амплітудно-частотну характеристику

і фазочастотну характеристику

.

При ω = 0 А_k(0) = 0,33; φ_k(0) = 0;

при ω = 1,517 А_k(1,517) =0,308; φ_k(1,517) = -0,195 ≈ -11°.

Так як у інтервалі ω[0; 1,517] годограф R_k(іω) проходить у четвертому квадранті, то в якості реального компенсатора можна вибрати аперіодичну ланку 1-го порядку або інтегро-диференцюючу ланку, АФХ яких також розміщується в четвертому квадранті (дивись табл.. 1.1 [1]).

1 випадок. Вибирають в якості реального компенсатора аперіодичну ланку 1-го порядку з передаточною функцією

,

з амплітудно-частотною характеристикою

,

з фазочастотною характеристикою

.

Параметри настройки реального компенсатора k, Т визначають із умови збігу АФХ реального та ідеального компенсаторів в робочому діапазоні частот.

При ω = 0 А(0) = k = А_k(0) = 0,33

звідси k = 0,33.

При ω = 1,517

тобто

. (2.18)

Система рівнянь (2.18) не має точного рішення. Приблизне рішення її, тобто приблизне значення параметра настройки Т знаходять за допомогою ітераційної процедури розрахунку. Значення Т перебирають доки не буде досягнута приблизно однакова відносна похибка кожного із рівнянь системи (2.18). У даному прикладі таким рішенням є Т = 0,137, для якого φ(1,517) = – 0,205, а А(1,517) = 0,323. Таким чином, параметри настройки аперіодичної ланки 1-го порядку як реального компенсатора мають значення

k = 0,33; Т = 0,137.

2 випадок. Вибирають в якості реального компенсатора інтегро-диференцюючу ланку з передаточною функцією.

(Т₁ < Т₂)

з амплітудно-частотною характеристикою

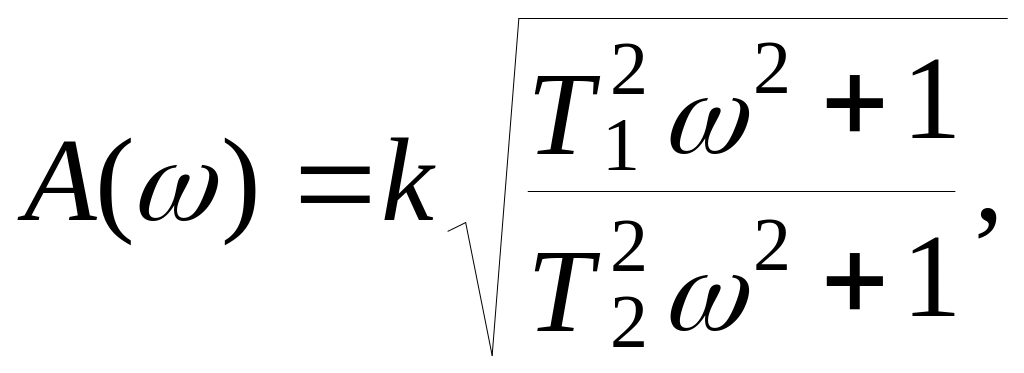
з фазочастотною характеристикою

Параметри настройки інтегро-диференцюючої ланки Т₁ і Т₂ визначають із умови збігу АФХ реального та ідеального компенсаторів в робочому діапазоні частот.

При ω = 0 А(0) = k = А_k(0) = 0,33

звідси k = 0,33.

При ω = 1,517

.

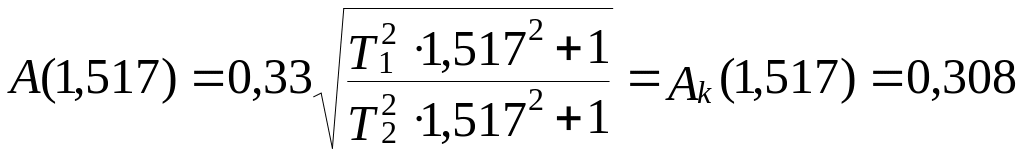
Тобто 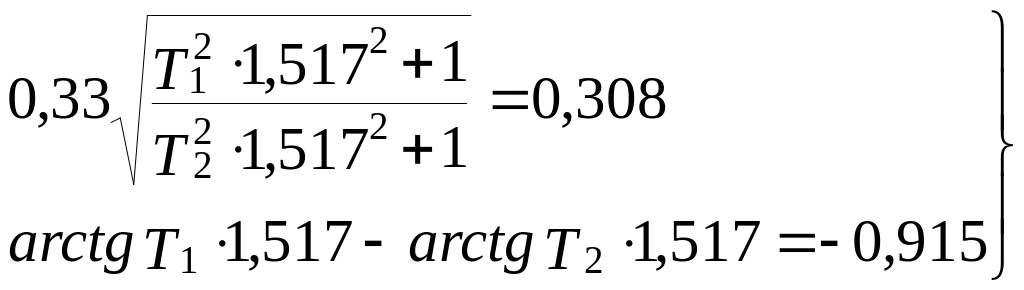(2.19)

Розв’язуючи систему рівнянь (2.19) знаходять Т₁ та Т₂. Для цього перетворюють систему (2.19), виділивши із першого рівняння вираження для Т₂. Система рівнянь прийме вигляд

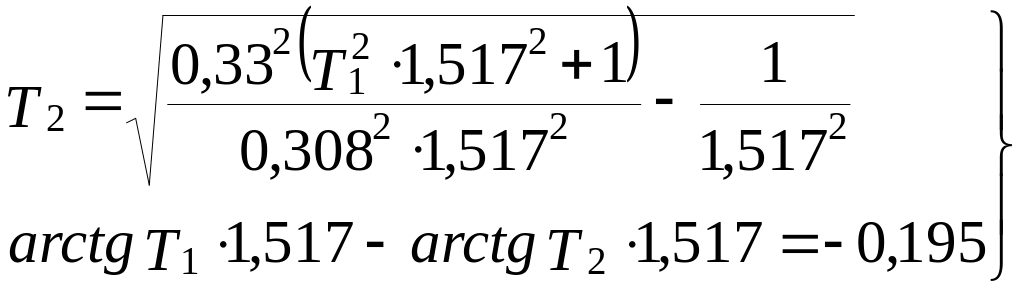(2.20)

Систему рівнянь (2.20) розв’язують, застосовуючи ітераційну процедуру.

I цикл розрахунку. Задаються значенням Т₁ = 0,06, розраховують з першого рівняння Т₂ = 0,26. Підставляють значення Т₁ і Т₂ у друге рівняння, розраховують φ(1,517) = –0,280 < –0,195.

Результати II циклу розрахунку

Т₁ = 0,20; Т₂ = 0,33; φ(1,517) = –0,169 > –0,195.

Результати III циклу

Т₁ = 0,16; Т₂ = 0,305; φ(1,517) = –0,195.

Результати III циклу розрахунку і є рішенням системи рівнянь (2.20).

Таким чином, параметри настройки інтегро-диференцюючої ланки як реального компенсатора мають значення

k = 0,33; Т₁ = 0,16; Т₂ = 0,305.