2 Синтез комбінованих систем регулювання

2.1 Призначення та характеристика комбінованих аср

Комбіновані системи відносяться до багатоконтурних систем, тобто систем з додатковими інформаційними каналами. Вони складаються із розімкнутого і замкнутого контурів регулювання. Розімкнутий контур здійснює регулювання за збуренням і призначений для швидкої ефективної компенсації основних вимірюваних збурень і, як наслідок, для зменшення динамічної похибки регулювання. Замкнутий контур регулювання працює за відхиленням і призначений для компенсації усіх інших збурень і забезпечення високої статичної точності регулювання.

Комбіновані системи регулювання за структурою нагадують двокаскадні системи. Але необхідно пам’ятати, що вони принципово відрізняються від двокаскадних тим, що працюють за розімкнуто-замкнутим циклом, а в каскадних АСР обидва контури замкнуті.

Ефективність введення розімкнутого контуру регулювання для компенсації основного вимірюваного збурення залежить від співвідношення між величиною запізнювання за каналом регулювання τ_уμ і величиною запізнювання за каналом збурення τ_уλ . При збільшенні τ_уλ ефективність введення розімкнутого контуру регулювання зростає, динамічна похибка регулювання зменшується. При τ_уλ ≥ τ_уμ вплив збурення на регульовану величину може бути повністю скомпенсованим і буде забезпечена абсолютна інваріантність регульованої величини відносно даного вимірюваного збурення.

Існує дві структурні схеми комбінованих систем регулювання (рис. 2.1), які відрізняються одна від одної місцем підключення виходу компенсатора (регулятора розімкнутого контуру).

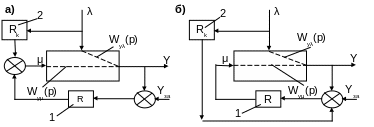
Рис. 2.1 Структурні схеми комбінованої АСР:

а) при підключенні виходу компенсатора до входу об’єкта; б) при підключенні виходу компенсатора до входу регулятора; 1-регулятор; 2-компенсатор

2.2 Задача і алгоритм синтезу комбінованих аср

Задача синтезу комбінованої АСР полягає у визначенні параметрів настройки регулятора замкнутої системи і передаточної функції компенсатора. Початковими даними для розв’язання задачі синтезу комбінованої АСР є відомі передаточні функції об’єкта керування за каналами збурення та регулювання і структура (закон регулювання) регулятора замкнутої системи.

Синтез комбінованої АСР виконується в такій послідовності:

Етап I: Визначення настройок регулятора замкнутої системи і робочої частоти в одноконтурній замкнутій системі регулювання. На цьому етапі приймається допущення, що основне збурення, до якого підключено компенсатор, відсутнє, так як у наступному етапі буде розраховано передаточну функцію компенсатора із умови повної компенсації цього збурення λ.

Для розв’язання задачі застосовується метод Циглера-Нікольса (метод незгасаючих коливань). Метод базується на визначенні критичного коефіцієнта передачі регулятора та критичної частоти, при яких автоматична система регулювання буде знаходитись на границі стійкості. Умова знаходження замкнутої АСР на границі стійкості

W_рс(іω) = 1 ,

або

W_уμ(іω) · R(іω) = 1 , (2.1)

де W_рс(іω) – амплітудно-фазова характеристика (АФХ) розімкнутої системи;

W_уμ(іω) – АФХ об’єкта за каналом регулювання;

R(іω) – АФХ регулятора.

Представляючи АФХ об’єкта та регулятора через амплітудно- та фазочастотні характеристики рівняння (2.1) можна замінити системою рівнянь

, (2.2)

де А_уμ(ω), А_R(ω,S) – амплітудно-частотні характеристики відповідно об’єкта та регулятора;

φ_уμ(ω), φ_R(ω,S) – фазочастотні характеристики відповідно об’єкта та регулятора;

S – коефіцієнт передачі регулятора.

Розв’язуючи систему рівнянь (2.2) визначають критичну частоту ω_кр і критичний коефіцієнт передачі регулятора S_кр , при яких замкнута АСР буде знаходитись на границі стійкості. Робочу частоту ω_р приймають приблизно рівною ω_кр , а оптимальний коефіцієнт передачі S_опт = 0,5 · S_кр для забезпечення необхідного запасу стійкості.

Етап II: Визначення передаточної функції ідеального компенсатора R_к(р) із умови інваріантності та аналіз можливості його фізичної реалізації.

Умова інваріантності системи у(t) = 0 випливає із аналізу структурної схеми (рис. 2.1) і запишеться відповідно:

для схеми (рис. 2.1 а)

(2.3)

де Y(р) – зображення з Лапласу сигналу у(t),

λ(р) – зображення з Лапласу сигналу λ(t)

для схеми (рис. 2.1 б)

. (2.4)

При наявності збурення [λ(р) ≠ 0] умови інваріантності (2.3, 2.4) виконуються, якщо:

для схеми (рис. 2.1 а)

, (2.5)

звідки ; (2.6)

для схеми (рис. 2.1 б)

, (2.7)

звідки . (2.8)

Структура "ідеального" компенсатора, яка визначається розрахованою за відповідними формулами (2.6, 2.8) передаточною функцією, може статися дуже складною, або зовсім непридатною до фізичної реалізації. Визначення можливості фізичної реалізації "ідеального" компенсатора здійснюється шляхом перевірки двох умов

τ_уλ ≥ τ_уμ , (2.9)

m ≤ n (2.10)

де τ_уλ , τ_уμ – запізнювання відповідно за каналом збурення і керування,

m, n – ступінь поліному відповідно в чисельнику та знаменнику передаточної функції компенсатора.

Якщо умови (2.9, 2.10) виконуються, то компенсатор може бути фізично реалізованим і навпаки.

Етап III: Вибір реального компенсатора і визначення його параметрів із умови наближеної інваріантності у робочому діапазоні частот.

На цьому етапі при неможливості або складності фізичної реалізації "ідеального" компенсатора його замінюють реальним компенсатором. В якості реального компенсатора вибирають відому ланку, яка легко реалізується фізично і має амплітудно-фазову характеристику, що розміщується в тому ж квадранті, що і АФХ "ідеального" компенсатора у робочому діапазоні частот. Параметри передаточної функції реального компенсатора визначаються із умови найбільшої близькості АФХ реального та "ідеального" компенсаторів в робочому діапазоні частот.