1.3 Приклад синтезу двокаскадної аср

1.3.1 Умова задачі

Розрахувати приблизні настройки регуляторів в двокаскадній АСР, якщо передаточні функції об’єкта за основним та допоміжним каналами і передаточні функції регуляторів відповідно дорівнюють:

; ;

; .

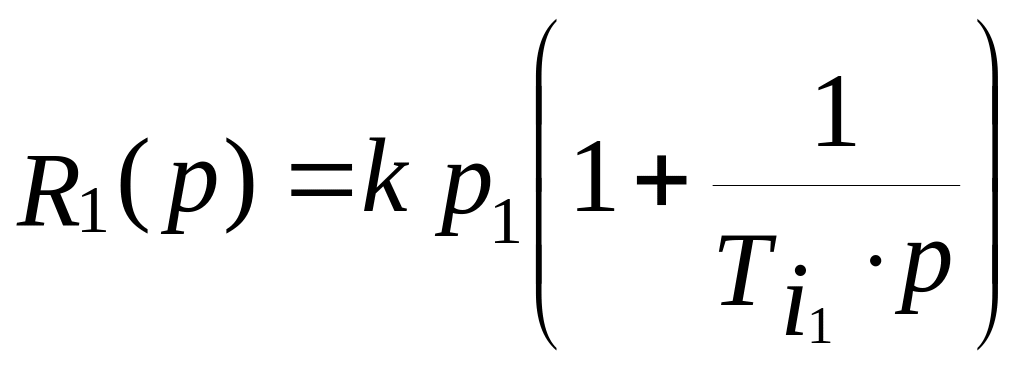1.3.2 Рішення задачі

Враховуючи, що швидкодія допоміжного контуру регулювання набагато більше, аніж основного вибирають I метод синтезу двокаскадної АСР. Розрахунок виконують за вищенаведеним алгоритмом:

1. Визначають приблизне значення передаточної функції еквівалентного об’єкта основного регулятора за вираженням (1.3)

.

2. Розраховують приблизні настройки основного регулятора, тобто виконують синтез одно контурної замкнутої системи з еквівалентним об’єктом. Визначають амплітудно-частотну та фазочастотну характеристики еквівалентного об’єкта

(1.6)

(1.7)

Результати розрахунків модуля та фази амплітудно-фазової характеристики (АФХ) еквівалентного об’єкта за формулами (1.6, 1.7) заносять у таблицю 1.1.

Таблиця 1.1

Дані для побудови АФХ еквівалентного об’єкта та розімкнутої системи

ω, рад/с	АФХ об’єкта		Вектор
	А0(ω)	φ0(ω), град.	Ті = 4 с	Ті = 6 с	Ті = 10 с
0,15	0,325	-71,0	0,541	0,361	0,217
0,20	0,272	-85,2	0,340	0,227	0,136
0,30	0,204	-108,9	0,170	0,113	0,068
0,40	0,165	-128,8	0,103	0,069	0,041
0,50	0,141	-148,1	0,070	0,047	0,028

Будують АФХ об’єкта за даними таблиці 1.1 у вибраному масштабі (рис. 1.1). Точки характеристики А₁, А₂, А₃,... для відповідних частот з’єднують з початком координат відрізками ОА₁, ОА₂, ОА₃,....

Для побудови АФХ розімкнутої системи з коефіцієнтом підсилення регулятора k_р = 1 і деяким заданим часом інтегрування Т_і розраховують вектор

(1.8)

Результати розрахунку заносять у таблицю 1.1. До відрізків ОА₁, ОА₂, ОА₃,... встановлюють перпендикуляри, на яких у вибраному масштабі відкладають вектори ΔА(ω) і з’єднують отримані точки плавною кривою.

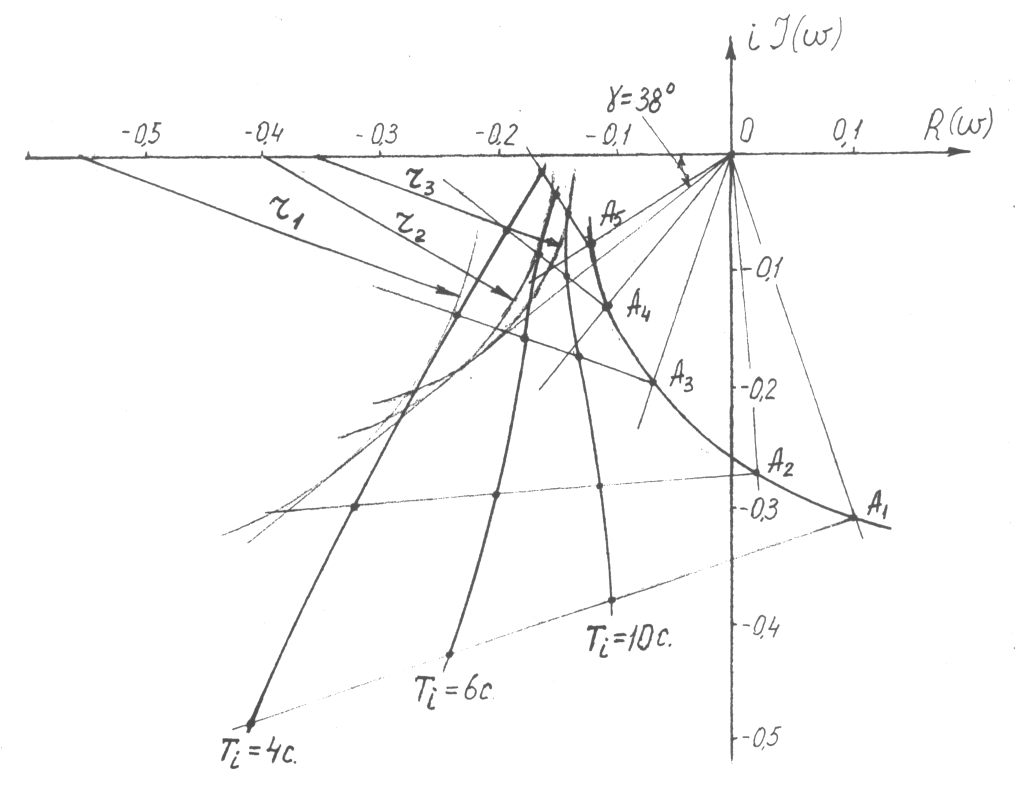
Рис. 1.1. Визначення настройок основного регулятора графоаналітичним методом

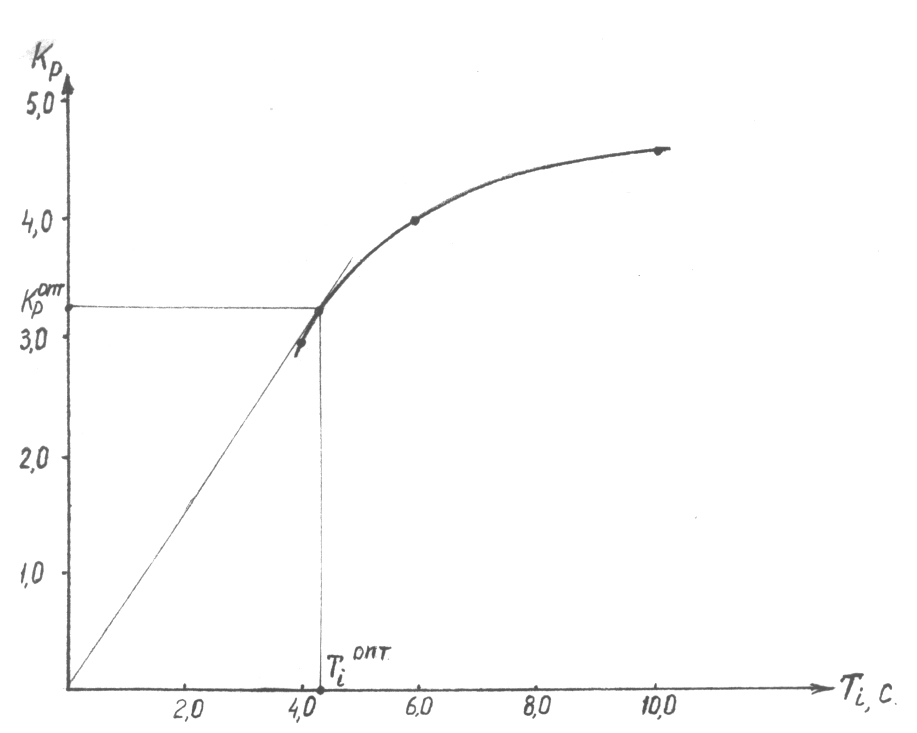
Рис. 1.2. Границя зони заданої ступені коливальності

Вибирають ступінь коливальності (наприклад, М ≈ 1,6) з початку координат проводять пряму лінію під кутом до дійсної від’ємної напіввісі. Будують кола з центрами на цій вісі, які одночасно дотикаються відповідних АФХ розімкнутих систем і прямої, проведеної під кутом 38°. Визначені у відповідності з масштабом радіуси кіл r_і та розраховані коефіцієнти передач регулятора за формулою

записують у таблицю 1.2.

Таблиця 1.2

Ті , с	rі
4	0,342	2,9
6	0,247	4,0
10	0,217	4,6

За результатами розрахунку в площині параметрів настройки регулятора будують границю зони заданої ступені коливальності (гасіння) (рис. 1.2) і проводять дотичну із початку координат цієї границі. Точка дотику і визначає оптимальні параметри настройки

k_р^опт = 3,25 Т_і^опт = 4,3 с.

4. Знаходять приблизну передаточну функцію еквівалентного об’єкта допоміжного регулятора W₁^екв.0(р) за вираженням (1.4)

.

5. Розраховують приблизні настройки допоміжного регулятора за відомими формулами [3] для типового перехідного процесу регулювання з мінімальною площею відхилення

с.

На цьому перший цикл розрахунку і в цілому розв’язання задачі закінчується. Визначені настройки регуляторів

с

с.