1. Общие указания

В процессе изучения дисциплины «Статистика» студенты заочной формы обучения в рамках часов самостоятельной работы выполняют письменную контрольную работу, которая должны отвечать следующим требованиям:

1. Выполненная работа предоставляется на проверку после последнего практического занятия, на котором разбирается решение всех типов задач.

2. В начале работы указывается соответствующий номер варианта.

3. Задачи необходимо располагать в том же порядке, в каком они даны в задании. Перед решением задачи должно быть полностью приведено ее условие.

4. Решение задачи должно сопровождаться необходимыми формулами, развернутыми расчетами и краткими пояснениями. Задачи, к которым даны ответы без развернутых расчетов, пояснений и кратких выводов, будут считаться нерешенными. Решение задач следует по возможности оформлять в виде таблиц.

5. Все расчеты относительных показателей нужно производить с принятой в статистике точностью до 0,001, а проценты – до 0,1.

6. Выполненная работа должна быть оформлена аккуратно, написана разборчиво, чисто, без помарок и зачеркиваний. Запрещается произвольно сокращать слова (допускаются лишь общепринятые сокращения). Все приводимые таблицы надо оформлять в соответствии с правилами, принятыми в статистике. Страницы работы должны быть пронумерованы и иметь достаточно широкие поля для замечаний рецензента и исправлений (дополнений), вносимых студентом после рецензирования.

7. При правильном выполнении заданий работа оценивается отметкой «зачтено».

8. К экзамену допускаются студенты получившие отметку «зачтено» по контрольной работе.

Если студент не может самостоятельно выполнить контрольную работу или какую-то ее часть, следует обратиться к преподавателю за консультацией в установленные графиком дни.

2. Методические указания к выполнению контрольной работы

Целью контрольной работы является закрепление теоретических знаний, полученных студентами на занятиях и в процессе работы с литературой по следующим темам:

1. Статистическая сводка. Группировка. Таблицы.

2. Статистические показатели.

3. Средние величины.

4. Статистическое изучение вариации.

5. Выборочный метод в статистике.

6. Статистическое изучение динамики социально-экономических явлений.

7. Индексный метод в статистических исследованиях.

8. Графический метод изучения статистических данных.

Задания к самостоятельной индивидуальной работе составлены в 6 вариантах.

Выбор варианта зависит от начальной буквы фамилии студента:

Номер выполняемого варианта	Начальная буква фамилии студента
1	А, Ка, Т, Х, Ж
2	Б, К, М, Ц, У, С
3	В, Ко, Л, Н, Ч, Ю, Я
4	Г, О, Ш, Ф
5	Д, Ку, П, Щ, З
6	Е, И, Р, Э

При написании контрольной работы, прежде всего, рекомендуется ознакомиться с соответствующими разделами программы данного курса, методическими указаниями, разработанными кафедрой по отдельным темам, а также изучить рекомендуемую литературу, при этом уделив особое внимание методам построения статистических показателей и их анализу.

Каждый вариант контрольной работы состоит из 7 задач по наиболее важным темам раздела «Статистика».

Задача 1 составлена на тему «Статистическая сводка, метод группировок». При решении этой задачи необходимо понять суть аналитической группировки. Методом аналитической группировки устанавливается наличие взаимосвязи между факторным и результативным признаками. При этом следует иметь в виду, что в основу группировки берется факторный признак.

Группировка начинается с построения макета групповой аналитической таблицы, затем определяется интервал группировки по факторному признаку. Для заполнения макета аналитической таблицы необходимо построить рабочую таблицу, в которой происходит весь процесс группировки, затем полученные результаты оформляются в виде групповой аналитической таблицы. При составлении таблиц необходимо ознакомиться с основными правилами построения и оформления статистических таблиц. Необходимо также сделать вывод по полученным результатам.

Задачи 2 и 3 составлены на применение средних величин.

В задаче 2 необходимо правильно использовать формулу средней арифметической или средней гармонической величины. Для этого нужно знать экономическое содержание рассчитываемого показателя. Например, средняя производительность одного рабочего рассчитывается отношением количества всей произведенной продукции к общей численности рабочих. Если в задаче имеются данные о средней выработке 1 рабочего и численности рабочих, то необходима формула средней арифметической взвешенной.

,

где х – средняя выработка 1 рабочего; f – численность рабочих, а если имеются данные о о средней выработке 1 рабочего и общем объеме произведенной продукции, то необходима формула средней гармонической взвешенной:

,

где x – средняя выработка 1 рабочего; w – количество произведенной продукции.

При выборе средней необходимо знать правило:

1. если известен сам варьирующий признак (x) и его количество (f) – нужна средняя арифметическая взвешенная;

2. если известен варьирующий признак (x) и общий объем усредняемого признака (w) – нужна средняя гармоническая.

При решении задачи 3 следует изучить значение моды и медианы – разновидностей средних величин. Мода ( ) – это наиболее часто встречающаяся величина признака. В интервальном вариационном ряду она рассчитывается по формуле:

,

где и – нижняя и верхняя границы модального интервала; – частота интервала, предшествующего модальному; – частота модального интервала; – частота интервала, следующего за модальным.

Медиана ( ) – это середина ранжированного статистического ряда. В интервальном вариационном ряду она рассчитывается по формуле:

,

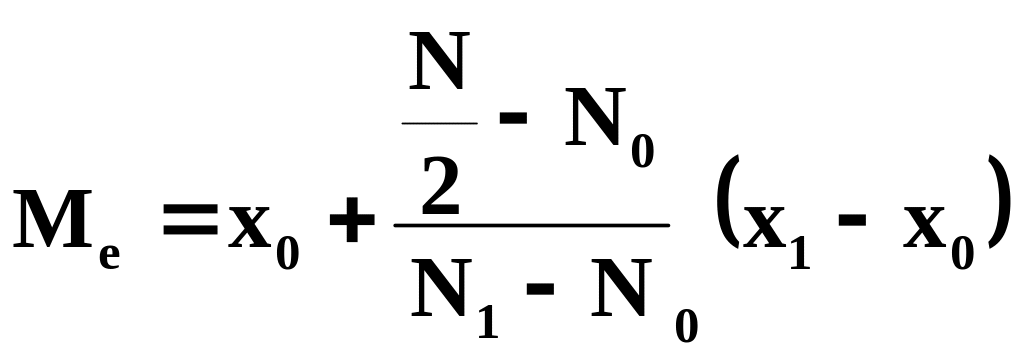где и – нижняя и верхняя границы медианного интервала; – общая численность вариант; – накопленная численность вариант до начала медианного интервала; – накопленная численность вариант до конца медианного интервала.

Значение моды и медианы можно определить также графически: моду – при помощи построения гистограммы, медиану – при помощи построения кумуляты.

Для решения задачи 4 необходимо изучить темы «Средние величины и показатели вариации».

По данным интервального вариационного ряда распределения необходимо исчислить среднюю дисперсию, среднее квадратическое отклонение обычным способом или способом моментов. При исчислении показателей способом моментов необходимо правильно понять момент первого и второго порядка.

Формула средней величины:

.

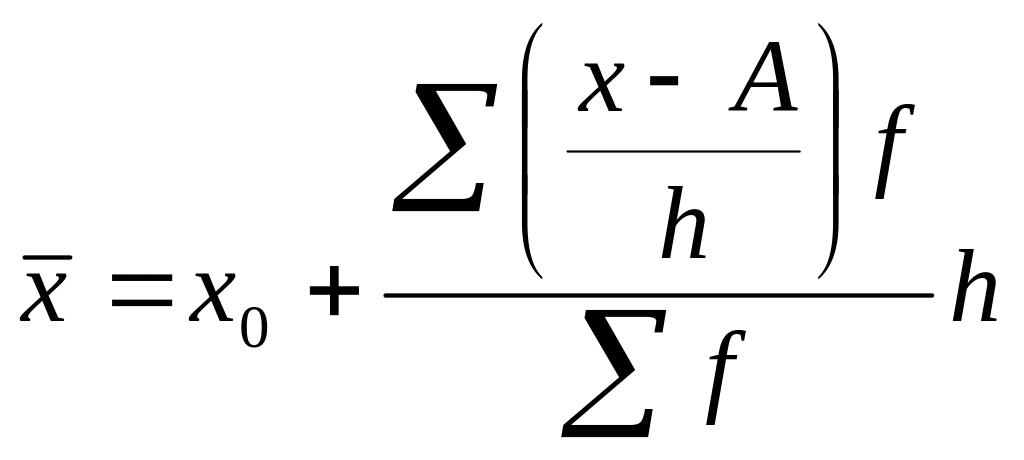При определении среднего значения признака по группам необходимо знать, что величина открытого интервала первой группы приравнивается к величине интервала второй группы, а величина открытого интервала последней группы – к величине интервала предпоследней группы.

Формула дисперсии способом моментов:

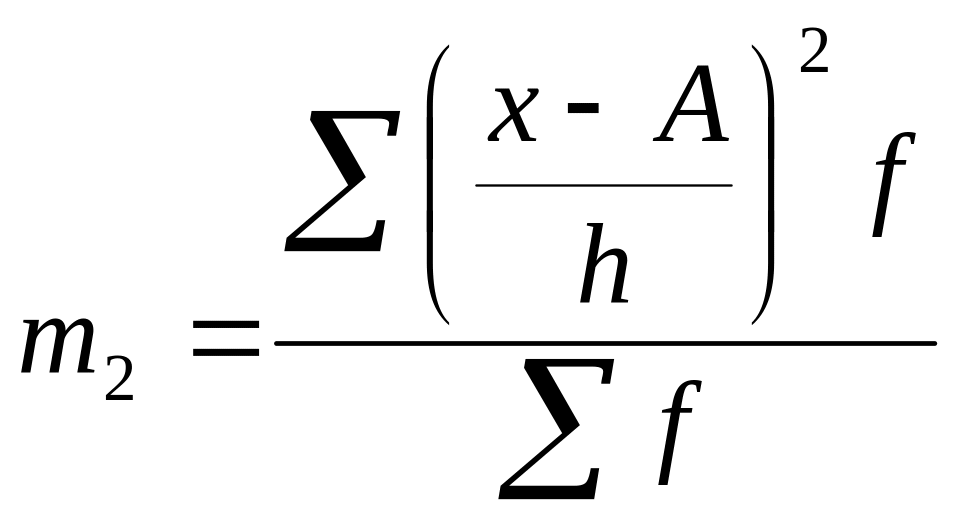
где – значение варьирующего признака; А – значение варианта с наибольшей частотой; – среднее значение варьирующего признака;

– частота; – величина (шаг) интервала.

Задача 5 составлена по теме «Выборочное наблюдение». Для расчета ошибок репрезентативности нужно изучить тему «Выборочное наблюдение», понять значение генеральной и выборочной совокупности, способы механического и случайного отбора и его варианты: бесповторный и повторный. При бесповторном способе отбора для определения предельной ошибки репрезентативности средней величины применяется формула:

,

где – предельная ошибка репрезентативности; – дисперсия в выборке; – численность генеральной совокупности; – численность выборки, t – коэффициент доверия, связанный с вероятностью.

При вероятности (Р):

Р1=0,683 t=1

Р2=0,954 t=2

Р3=0,997 t=3

Р4=0,999 t=4

Возможная граница генеральной средней определяется: нижняя ( ), верхняя ( ).

Предельная ошибка репрезентативности для доли:

,

где – доля данного признака в выборке.

Возможная граница генеральной доли: нижняя ( ), верхняя ( ).

Задача 6 составлена на тему «Динамические ряды» – на расчет и усвоение аналитических показателей динамических рядов, либо на применение методов их анализа. В условии задачи дан динамический ряд (интервальный или моментный), для исчисления среднего уровня динамического ряда (у) применяются (соответственно) средняя арифметическая

.

или средняя хронологическая

.

В зависимости от задачи исследования показатели динамики рассчитываются цепные (по отношению к предыдущему периоду) или базисные (по отношению к одному периоду, принятому за базу). Часто у студентов возникают трудности, связанные с исчислением средней показателей динамики. Необходимо иметь в виду, что средний абсолютный прирост ( ) рассчитывается двумя способами:

а) как средняя арифметическая из цепных абсолютных приростов ( ), т. е.

.

б) делением базисного прироста на число периодов

.

Средний темп роста ( ) рассчитывается также двумя способами:

а) по средней геометрической

,

где Тр – цепные коэффициенты роста; n – число коэффициентов роста.

б) так как произведение цепных темпов роста равно конечному базисному, то под корнем может быть базисный темп роста, исчисленный отношением Ук/Ун, и формула для расчета среднегодового темпа роста примет вид:

,

где n – число уровней ряда.

При анализе рядов динамики особое внимание уделяют выявлению плавной линии развития данного явления, характеризующую основную тенденцию его динамики. Для этого используют метод аналитического выравнивания по прямой. Уравнение прямой линии имеет вид:

,

где – значение уровней выровненного ряда; – показатели времени; – параметры прямой.

Для нахождения параметров используют систему нормальных уравнений:

.

При условии, что , уравнения имеют упрощенный вид:

,

откуда

.

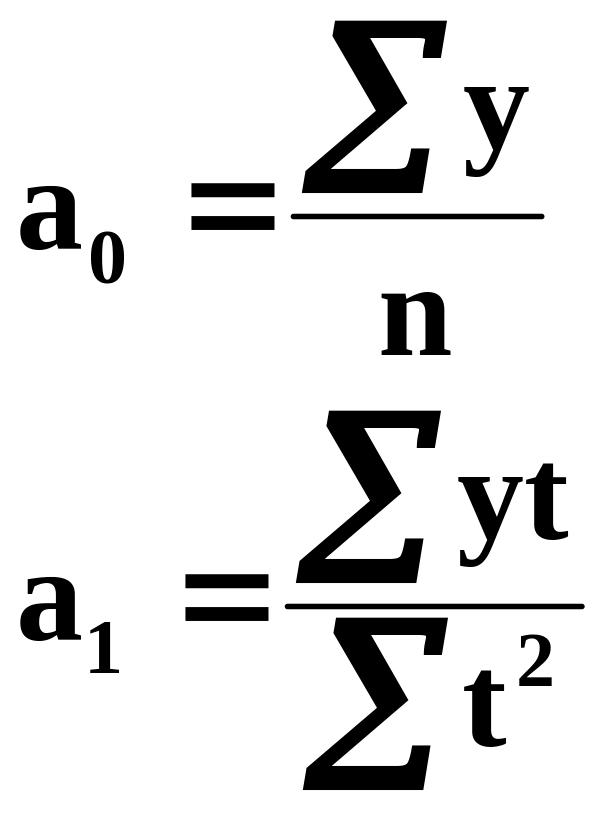Определив параметры и , легко вычислить теоретические уровни, т. е. ординаты точек искомой прямой.

Эмпирические (исходные) и теоретические уровни наносят на общий график. Направление прямой линии будет свидетельствовать об основной тенденции развития явления.

Задача 7 составлены на тему «Индексы». В зависимости от условия задачи могут применяться взаимосвязанные индексы. Например:

1. Общий индекс стоимости (товарооборота)

.

2. Общий индекс цен

.

3. Общий индекс физического объема

.

Взаимосвязь индексов:

.

При исчислении индексов по агрегатной форме при выборе весов необходимо учесть, что если в роли весов выступает качественный показатель (цена, себестоимость и др.), то он берется на уровне базисного периода, если количественный, то – на уровне отчетного. Вторая часть задачи составлена на исчисление индексов переменного, постоянного состава и влияния структурных сдвигов. Индекс переменного состава (цен, себестоимости) – это отношение средних показателей одноименной продукции по нескольким предприятиям, например, общий индекс цен:

.

Он отражает одновременно влияние двух факторов: изменение цен на одноименную продукцию и изменение удельного веса выпускаемой продукции на каждом предприятии в отчетном периоде. Для выявления каждого из перечисленных факторов исчисляются индексы цен постоянного (фиксированного) состава и индекс влияния структурных сдвигов:

,

.

Взаимосвязь индексов:

.