14.4.2.Подбор математической модели тренда и выявление его формы
Исключение случайных колебаний значений уровней ряда осуществляется с помощью нахождения «усредненных» значений. Способы устранения случайных факторов делятся на две больше группы:
Способы «механического» сглаживания колебаний путем усреднения значений ряда относительно других, расположенных рядом, уровней ряда (метод укрупнения интервалов, метод скользящей средней);
Способы «аналитического» выравнивания (графический метод или метод наименьших квадратов), т.е. определения сначала функционального выражения тенденции ряда, а затем новых, расчетных значений ряда.
Суть их в том, чтобы исключить из линии тренда случайные отклонения и выявить основное направление развития явления или процесса.
Подробнее ознакомимся с методом скользящей средней.
Последовательность определения скользящей средней:
- определяют количество временных промежутков, включаемых в укрупненный интервал;
- рассчитывают средний уровень для каждого укрупненного интервала. Интервалы последовательно, начиная с первого ряда, включают в себя следующие уровни ряда и исключают предыдущие. Считают, что расчетный средний уровень относится к середине укрупненного интервала;
- если количество промежутков времени, включенных в укрупненный интервал четное, то выполняется центрирование расчетных уровней ряда. Центрирование – определение средней арифметической простой из двух, расположенных рядом значений расчетных средних уровней ряда;
- определяют по полученным средним (или центрированным) уровням ряда основную закономерность.
Выше мы доказали, что в ряде динамики «Изменение заработной платы за 1991—2000 гг.» тренд хоть и с малой вероятностью существует.
Попробуем отразить это графически:
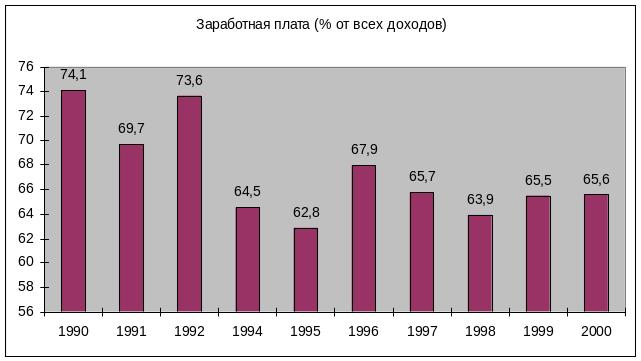
Пока форма тренда не прослеживается, т.к. налицо значительные колебания уровней заработной платы.
Для того, чтобы убрать нетипичные колебания применим метод трехчленной скользящей средней: будем брать по три уровня ряда динамики и находить среднее арифметическое. Первый трехчлен — это значения за 1991, 1992, 1993 г., второй трехчлен — значения за 1992, 1993, 1994 г., третий трехчлен — значения за 1993, 1994, 1995 и т.д. Т.к. в каждом последующем трехчлене исключается нижний уровень и включается следующий по списку.
|
1990 |
1991 |
1992 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
Заработная плата (% от всех доходов) |
74,1 |
69,7 |
73,6 |
64,5 |
62,8 |
67,9 |
65,7 |
63,9 |
65,5 |
65,6 |
Трехчленные скользящие средние |
|
72,5 |
69,3 |
66,97 |
65,1 |
65,5 |
65,8 |
65,03 |
65 |
|
Тогда график будет выглядеть следующим образом:
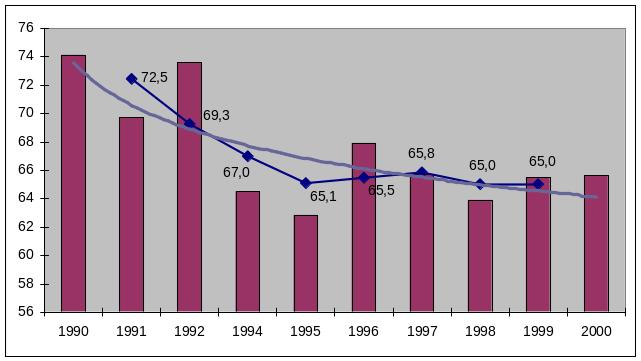
Синим цветом обозначена сглаженная методом скользящей средней линия тренда, которая достаточно приближена к математической модели (фиолетовый цвет) — гиперболической функции.
Вывод: для данного ряда динамики характерно монотонное убывание уровней, т.е. период с 1991 по 2000 гг. характеризуется закономерным процессом постепенного уменьшения заработной платы.
Методы «аналитического» сглаживания
Более точным способом
отображения тенденции динамического
ряда является аналитическое выравнивание,
т.е. выравнивание с помощью аналитических
формул. В этом случае динамический ряд
выражается в виде функции у(t), в которой
в качестве основного фактора принимается
время t, и изменения аргумента функции
определяют расчетные значения
.
Графический метод определения тренда включает следующие этапы:
1) нанести на поле координат (время – значение признака) точки,
соответствующие значениям признака в каждый период времени;
2) на основе визуальной оценки расположения точек на поле координат провести
линию, наиболее точно отражающую тенденцию распределения точек
(теоретически, это может быть и парабола, и гипербола и т.д., но фактически,
отобразить криволинейные зависимости, полагаясь на глазомер, достаточно
сложно);
3) выбрать на проведенной линии произвольные точки и, используя их координаты, записать и решить систему уравнений, определив, таким образом, параметры уравнения.
Параметры уравнения можно найти метод наименьших квадратов.
Метод наименьших квадратов включает следующие этапы:
1) рассчитать параметры уравнений по каждому из предполагаемых вариантов и
записать соответствующие уравнения;
2) рассчитать сумму квадратов отклонений фактических значений признака от
теоретических по каждому из предполагаемых вариантов и выбрать вариант
уравнения, которому соответствует минимальное значение суммы квадратов
отклонений;
3) записать уравнение динамики.