10.6. Необходимая численность выборки

На практике для реализации выборочного наблюдения исследователем задаются:

- степень точности исследования (вероятность);

- предельная ошибка, т.е. интервал отклонения, определяемый целями исследования.

Исходя из этих критериев, рассчитывается необходимая численность выборочной совокупности (n) на основе формулы предельной ошибки выборки. Как указывалось выше, предельная ошибка выборки определяется для средней величины ( ) и для доли (w), то, соответственно, имеем два варианта определения необходимой численности выборочной совокупности:

а) для повторного отбора:

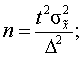
б) для бесповторного отбора:

.

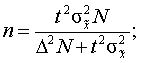
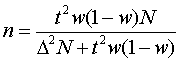10.7. Понятие о малой выборке

В практике статистического исследования иногда необходимо сделать выводы по малому числу наблюдений. Это может быть связано с ограниченностью ресурсов на проведение выборки, или с ограниченным доступом к объекту исследования.

Если объем выборки 30 единиц и меньше (такие выборки называются малыми), то распределение выборочных средних значений признака (а, следовательно, отклонений от средней ошибки) не описывается нормальным законом. Расчет показателей для малой выборки осуществляется с применением специальной методики, учитывающей распределение вероятностей появления ошибок определенных размеров.

Распределение ошибок выборочных оценок при небольших объемах выборки называют распределениями Стьюдента по имени их исследователя.

Расчет предельной ошибки для случаев, когда n 30 необходимо выполнять по правилам малой выборки. Предельная ошибка малой выборки рассчитывается по формуле:

, где - коэффициент доверия Стьюдента;

- выборочная дисперсия признака в малой выборке.

Значение коэффициента доверия Стьюдента находится по таблицам значений распределения Стьюдента по двум параметрам – степень значимости ( ) и числу степеней свободы (в данном случае n-1).

Поскольку при проведении малой выборки в качестве доверительной вероятности практически принимается значение 0,95 или 0,99, то для определения предельной ошибки малой выборки используются следующие показания распределения Стьюдента:

n
	0,95	0,99
4	3,183	5,841
5	2,777	4,604
6	2,571	4,032
7	2,447	3,707
8	2,364	3,500
9	2,307	3,356
10	2,263	3,250
15	2,119	2,921
20	2,078	2,832

10.8. Распространение результатов выборочного наблюдения результатов на генеральную совокупность.

Заключительным этапом выборочного наблюдения является распространение его результатов на генеральную совокупность.

Вывод о возможности распространения в значительной степени зависит от качества основы выборки, прежде всего от полноты. Существуют два основных метода распространения - прямой пересчет и способ коэффициентов.

Способ прямого пересчёта. Он состоит в том, что показатели выборочной доли или средней распространяется на генеральную совокупность с учётом ошибки выборки.

Так, в торговле определяется количество поступивших в партии товара нестандартных изделий. Для этого (с учётом принятой степени вероятности) показатели доли нестандартных изделий в выборке умножаются на численность изделий во всей партии товара.

Способ поправочных коэффициентов. Применяется в случаях, когда целью выборочного метода является уточнение результатов сплошного учета. В статистической практике этот способ используется при уточнении данных ежегодных переписей скота, находящегося у населения. Для этого после обобщения данных сплошного учета практикуется 10%-ное выборочное обследование с определением так называемого “процента недоучета”.

ГЛОССАРИЙ

Малая выборка – выборка размером меньше 30.

Многоступенчатая выборка – это выборка, которая формируется за несколько шагов.

Многофазовая выборка – это выборка, единицы которой обследуются по разному

набору признаков.

Однофазовая выборка – это выборка, все единицы которой обследуются по одному и

тому же набору признаков.

Одноступенчатая выборка – это выборка, которая формируется за один шаг.

Ошибки регистрации – ошибки, связанные с процессом сбора данных.

Ошибки репрезентативности – ошибки, связанные с тем, что оценки параметров всей

совокупности единиц выполняются на основе частичных, неполных данных.

Случайная механическая выборка выполняется по следующей процедуре. Все

единицы совокупности ранжируется по признаку, не связанному с изучаемым, и затем с

шагом n в выборочную совокупность отбирается каждая n-ная единица.

Случайная районированная (стратифицированная, типическая) выборка

предполагает пропорциональный отбор единиц из структурных частей генеральной

совокупности.

Собственно случайная выборка выполняется посредством жеребьевки, лотереи,

стандартной компьютерной программы генератора случайных чисел либо таблицы

случайных чисел.

Вопросы для обсуждения.

1. Какое наблюдение называется выборочным?

2. В чем преимущества выборочного наблюдения перед сплошным?

3. Какие вопросы необходимо решить для проведения выборочного наблюдения?

4. Почему при выборочном наблюдении неизбежны ошибки и как они классифициются?

5. Каковы условия правильного отбора единиц совокупности при выборочном наблюдении?

6. Как производятся собственно-случайный, механический, типический и серийный отборы?

7. В чем различие повторной и бесповторной выборки?

8. Что представляет собой средняя ошибка выборки (для средней и доли)?

9. Что характеризует предельная ошибка выборки, и по каким формулам она исчисляется (для средней и доли)?

10. Что показывает коэффициент доверия?

11. Какими способами осуществляется распространение результатов выборочного наблюдения на всю совокупность?

12. Зачем и как исчисляются предельные статистические ошибки выборки (для средней и доли)?

13. По каким формулам определяется необходимая численность выборки, обеспечивающая с определенной вероятностью заданную точность наблюдения?